大模型从0到1|第九讲:扩展定律基础
大模型从0到1|第九讲:扩展定律基础

0. 课程概览与动机
回顾:Scaling Laws —— 既令人惊讶又有用!
- **数据扩展 (Data scaling)**:理解数据如何影响模型,背后有清晰的理论支持。
- **模型扩展 (Model scaling)**:极大地降低训练成本(避免在大模型上试错)。
- **扩展作为预测 (Scaling as prediction)**:理解哪些问题可以通过“暴力破解”(Brute force)解决。
想象一个场景…
假设你的朋友给了你 10,000 张 H100 GPU 一个月的使用权,让你构建一个好的开源语言模型 (LM)。
- 你组建了基础设施团队 (A2)。
- 你准备好了很棒的预训练数据集 (A4)。
- 核心问题:你该运行哪个大模型?(我们正处于这一步)
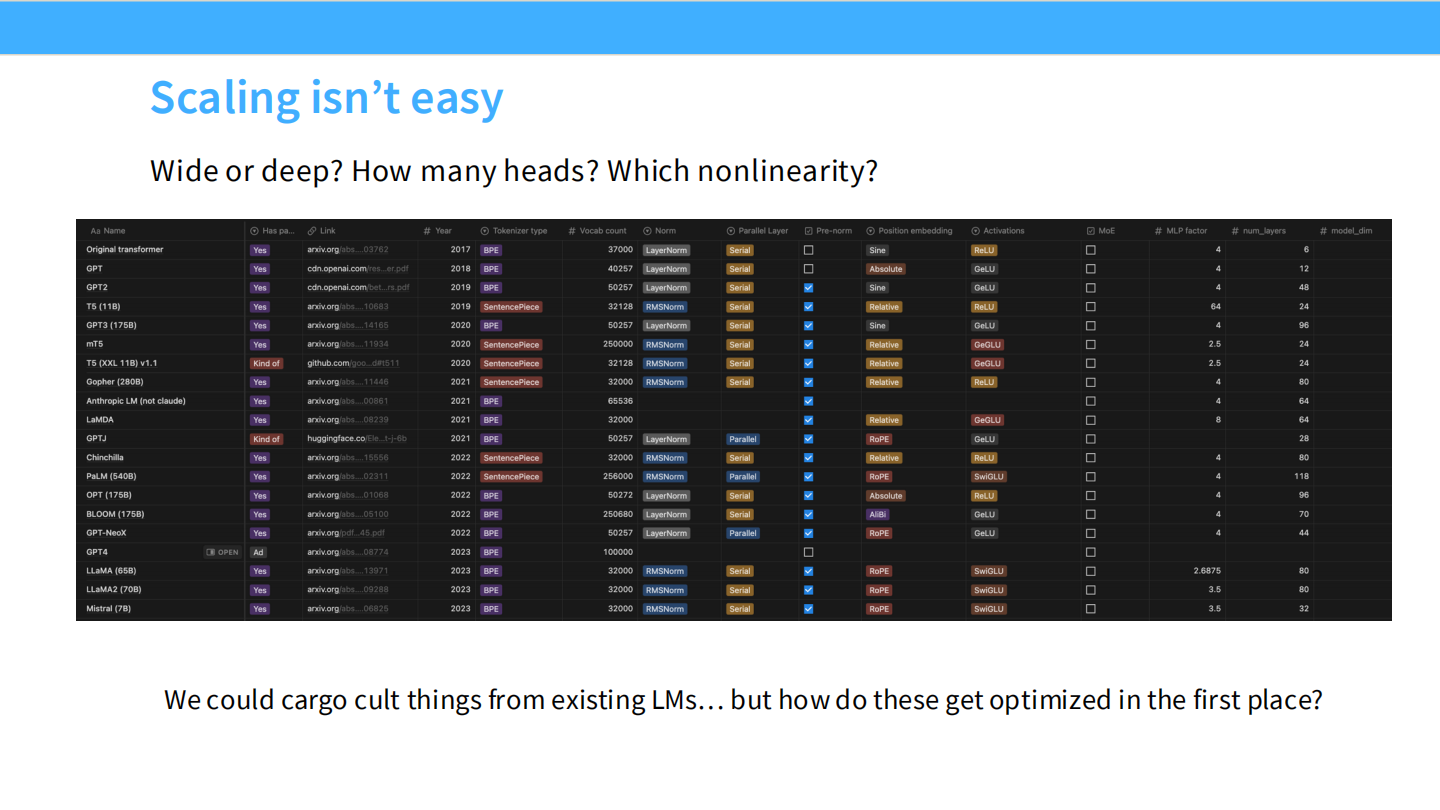
扩展并不容易 (Scaling isn’t easy)
看看历史上著名模型(GPT-3, T5, Gopher, Llama等)的参数配置:
- 宽还是深? (Wide or deep?)
- 多少个头? (How many heads?)
- 哪种非线性函数? (Which nonlinearity?)
我们不能只是盲目模仿(Cargo cult)现有的模型,我们需要知道它们是如何被优化出来的。
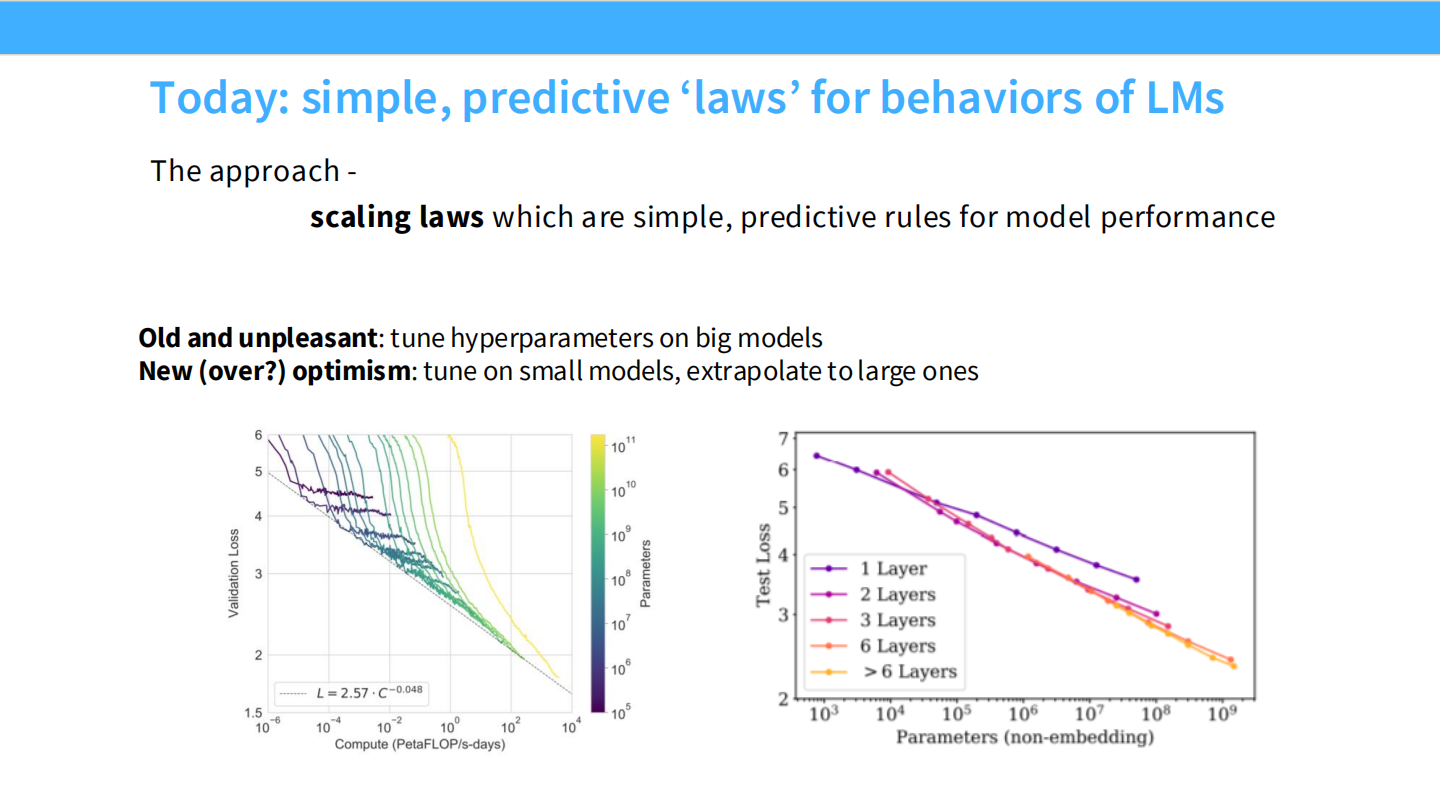
方法论:简单、可预测的“定律”
- 旧且痛苦的方法:在大模型上直接调整超参数。
- 新(且乐观)的方法:在小模型上调整,然后外推 (Extrapolate) 到大模型。
Part 1. 扩展定律的历史与背景 (History & Background)
理论基础:样本复杂度

理论家长期以来都在思考“Scaling”。
- 泛化界限:$\epsilon(\hat{h}) \le … \sqrt{\frac{1}{m}}$
- 但这些通常是**上界 (Upper bounds)**,而不是实际观察到的 Loss 值。
早期实证研究 (1993 - 2012)
- 1993 (Cortes et al.):最早发现测试误差随训练集大小呈现幂律 (Power-law) 衰减:$E_{test} = a + \frac{b}{n^\alpha}$。
- 2001 (Banko & Brill):在 NLP 任务中发现,性能与数据量呈对数线性 (Log-linear) 关系。结论:与其花钱开发算法,不如花钱开发语料库。
- **2012 (Kolachina et al.)**:在机器翻译中验证了幂律关系。
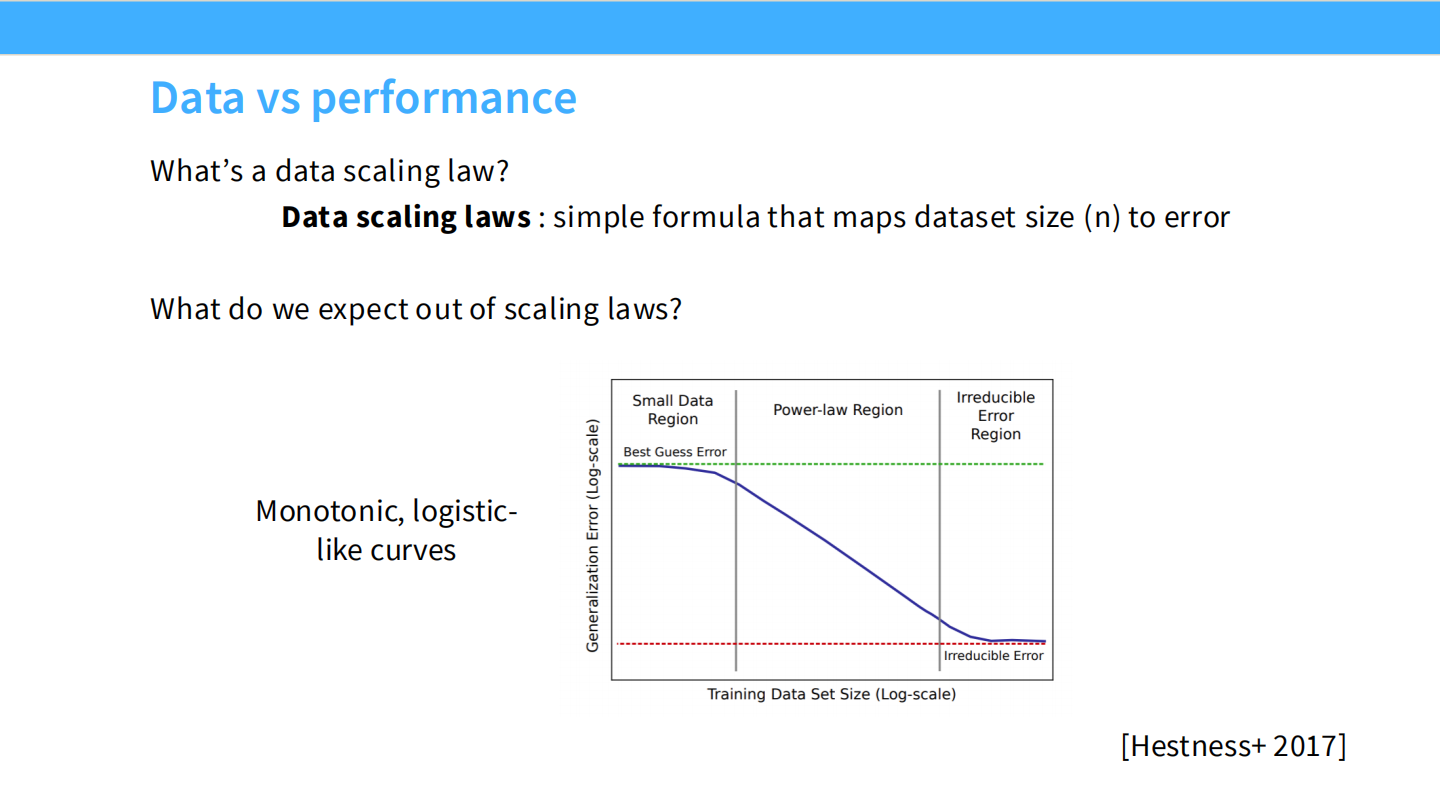
现代神经 Scaling 的开端:Hestness et al. (2017)

定义了学习曲线的三个区域:
- **小数据区 (Small Data Region)**:随机猜测。
- **幂律区 (Power-law Region)**:性能随数据量指数级提升。
- **不可约误差区 (Irreducible Error Region)**:性能饱和。
Hestness 的超前理念:
- **涌现 (Emergence)**:数据不够时模型看似没学到东西,容易出现“准确率悬崖”。
- 计算预测:可以预测达到特定精度所需的算力。
- 速度=精度:可以通过量化等手段牺牲精度换取速度,然后用更多的数据/更大的模型来弥补精度损失。
Part 2. 神经(LLM) Scaling 行为
核心观察:幂律关系无处不在
Kaplan et al. (2020) 展示了 Scaling Laws 适用于多种因素。
Test Loss 与以下因素在双对数坐标下呈线性关系:
- 计算量 (Compute)
- 数据集大小 (Dataset Size)
- 参数量 (Parameters)
数据扩展定律 (Data Scaling Laws)
公式:$L(D) \approx (D)^{-\alpha}$
即:双对数图上的线性关系(Scale-free / Power law)。
为什么是幂律?
- 理论推导:估计误差自然地以多项式速率衰减。例如均值估计的误差是 $1/n$。
- 指数之谜:经典统计模型(如回归)的 Scaling 指数通常是 1 ($1/n$)。但神经网络的指数(斜率)通常远小于 1 (如 0.095, 0.30)。
- **内在维度 (Intrinsic Dimensionality)**:Bahri (2021) 提出斜率 $\alpha$ 与数据的内在维度有关($\alpha \approx 1/d$)。维度越高,学习越慢。
其他数据扩展因素
**分布偏移 (Distribution Shift):
Kaplan (2021) 发现,数据构成(不同来源)影响的是曲线的截距 (Offset)**,而不是斜率。- Takeaway:收集多样化的高质量数据很重要,它决定了你的基线。
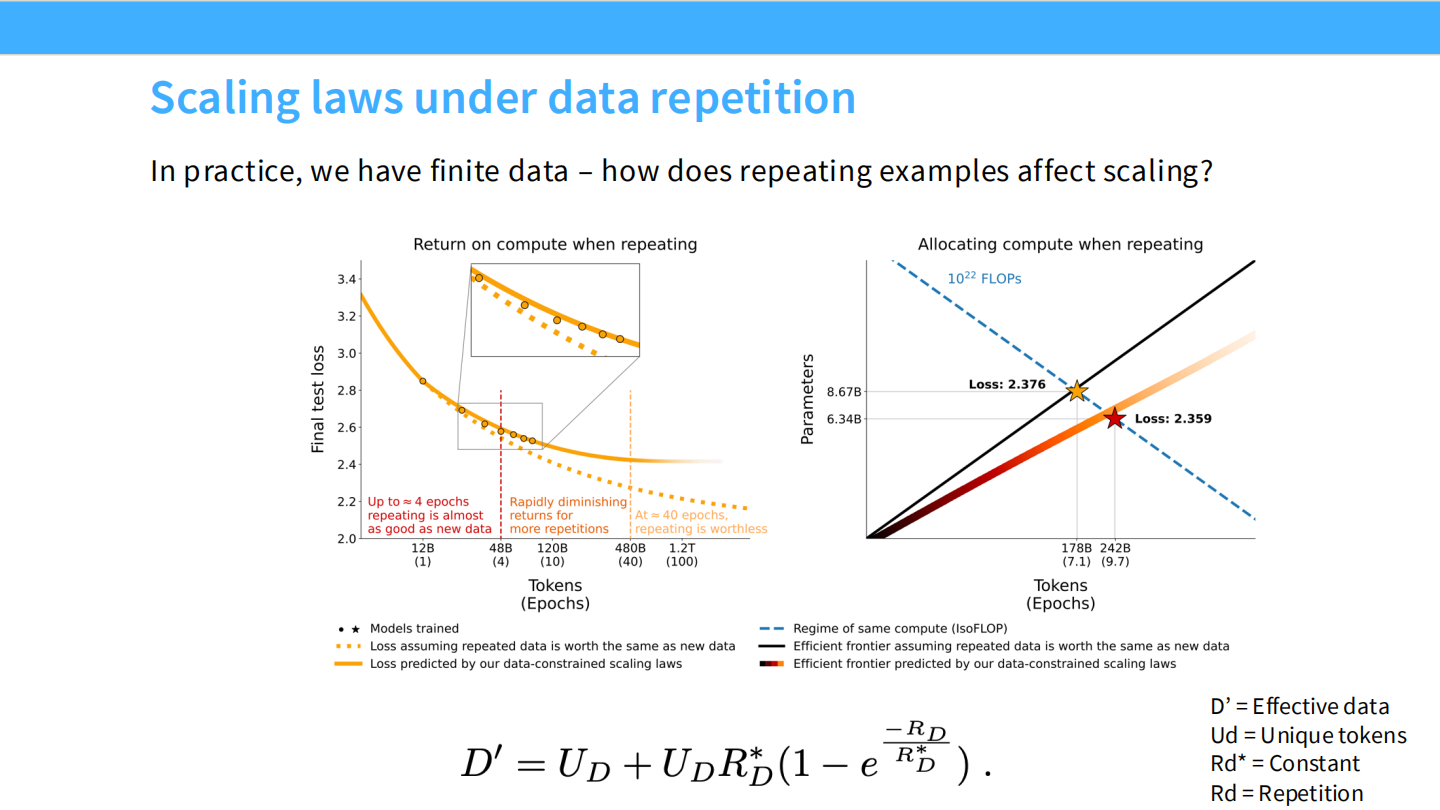
**数据重复 (Data Repetition)**:
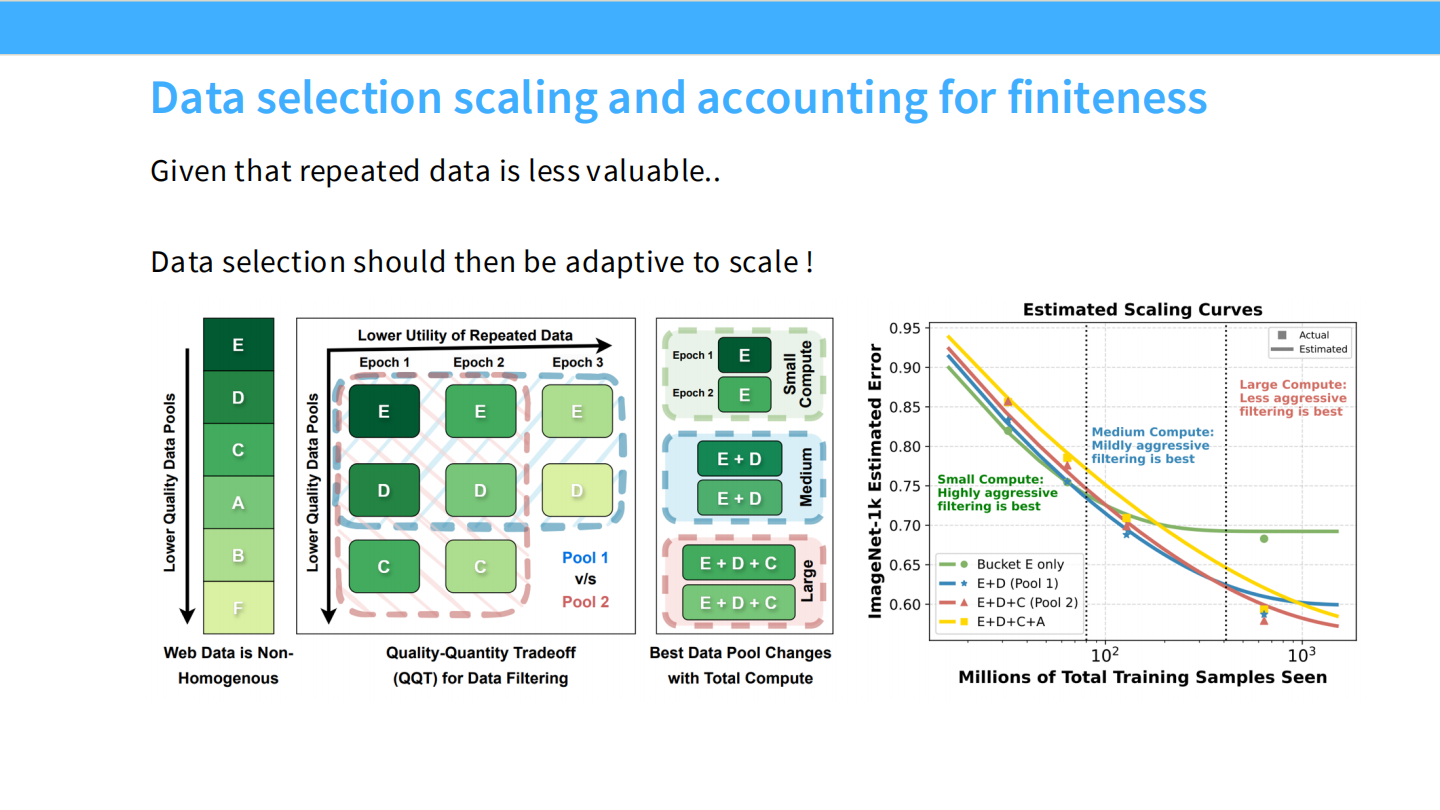
重复数据会导致收益迅速递减。大概在 4 个 Epoch 后,重复数据几乎不再带来提升。**数据选择 (Data Selection)**:

数据过滤策略应适应规模:- 小算力:不需要太挑剔,可以使用重复数据。
- 大算力:需要极高质量的数据,尽量避免重复。
Part 3. 模型工程的 Scaling Laws (Model Engineering)
动机
我们如何通过 Scaling Laws 来回答工程问题:选 LSTM 还是 Transformer?选 Adam 还是 SGD?
1. 架构选择 (Architecture)
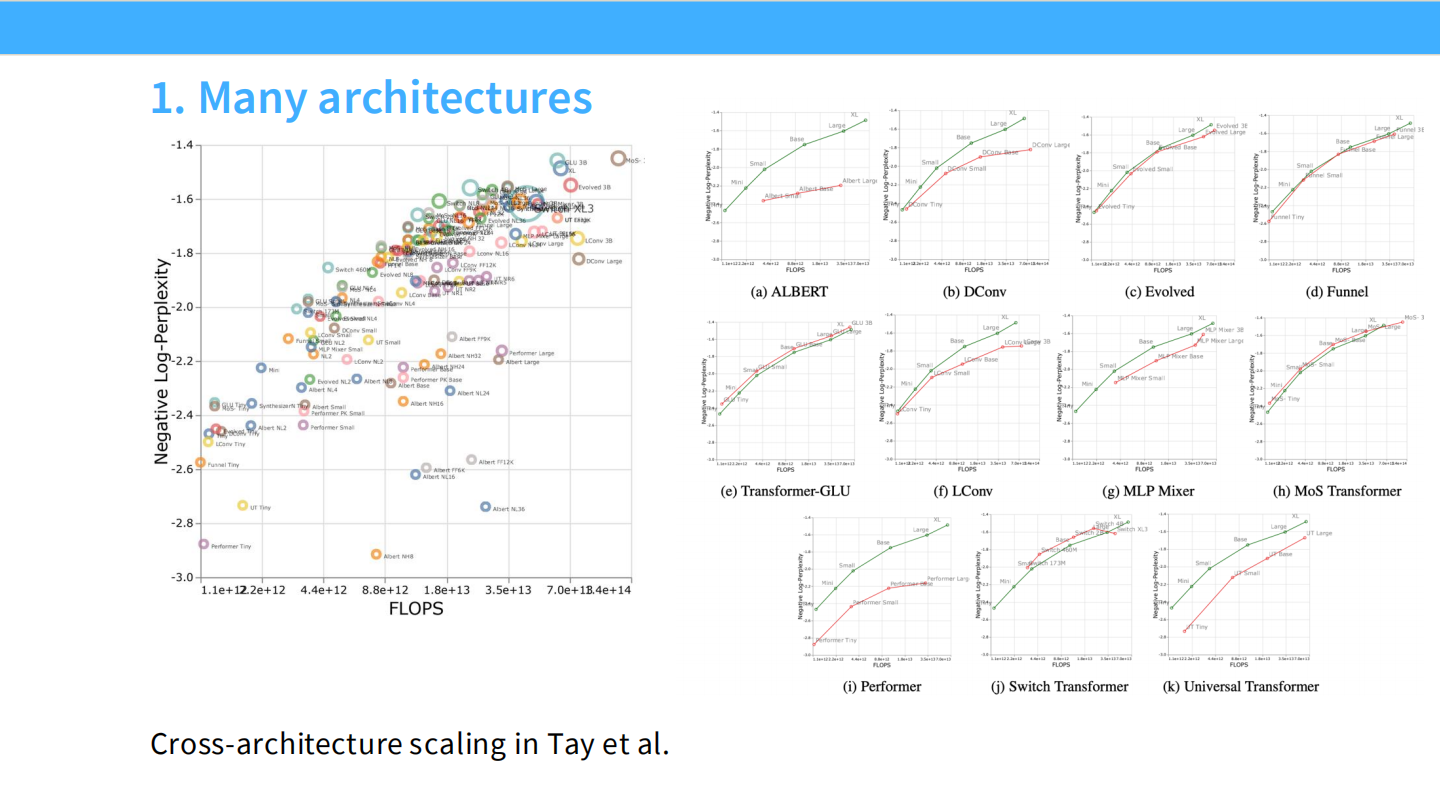
- Transformer vs LSTM:在相同算力下,Transformer 的 Loss 更低,且扩展斜率更陡(Scaling 更好)。
- 不同 Transformer 变体:Tay et al. 展示了不同架构(如 Switch Transformer, MLP Mixer)有不同的 Scaling 效率。
2. 优化器选择 (Optimizer)
- Adam vs SGD:Adam 不仅收敛快,而且 Scaling 曲线优于 SGD。
3. 深度与宽度 (Depth / Width)
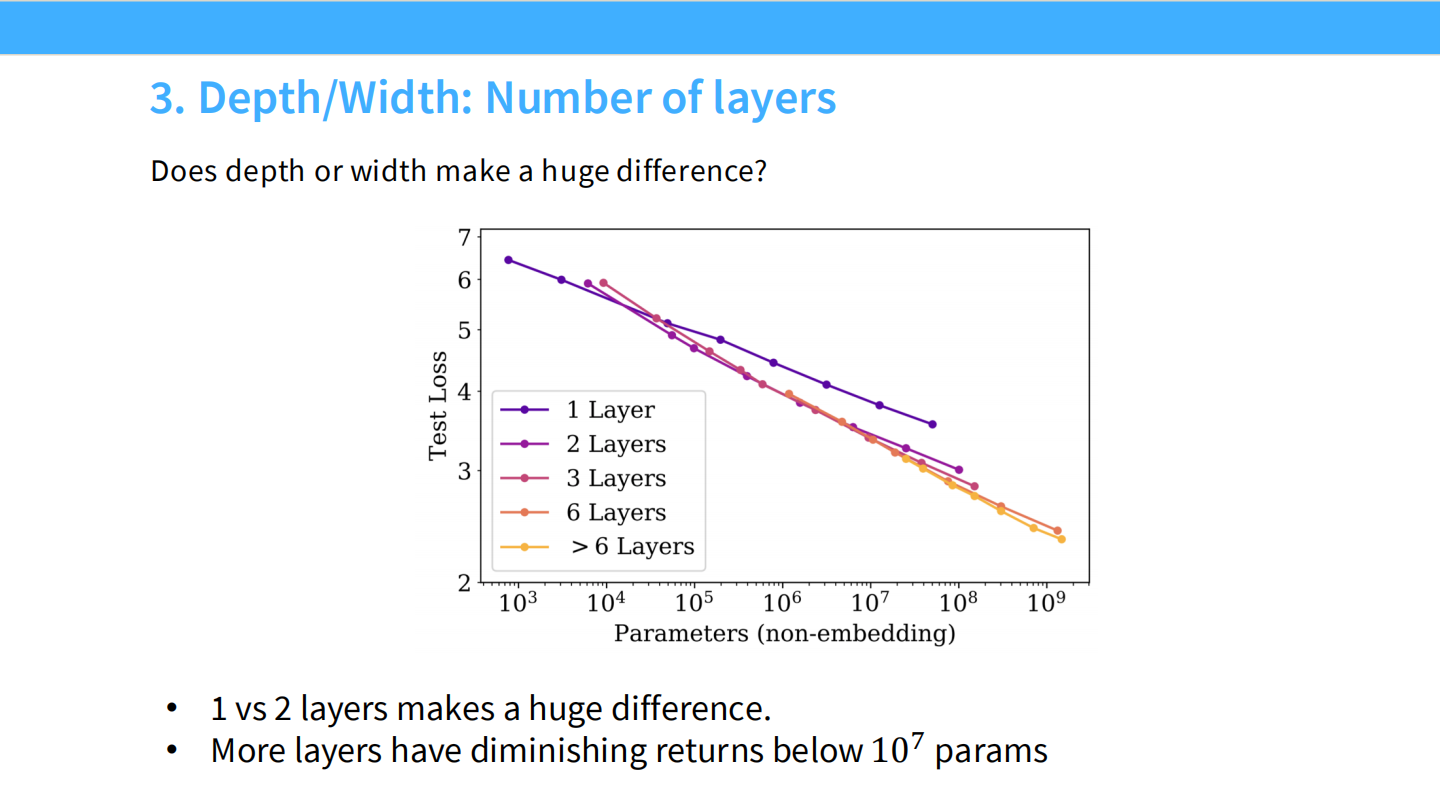
- 层数:1层和2层差别巨大。但在 $10^7$ 参数以上,增加层数的边际收益递减。
- 长宽比 (Aspect Ratio):只要不极端,模型的形状(深窄 vs 浅宽)对性能影响极小(Loss 变化 < 3%)。这给了工程并行化很大的自由度。
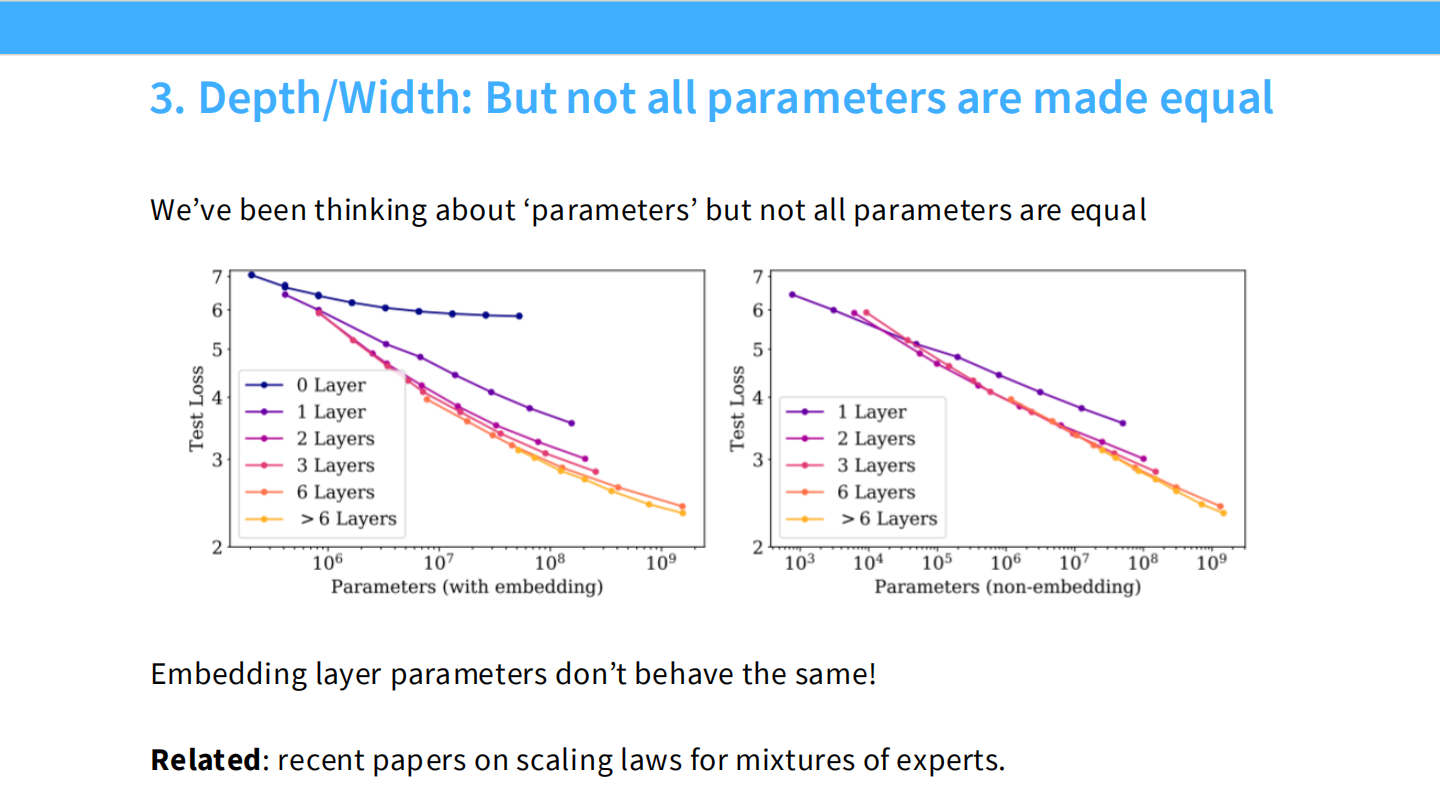
- 注意:Embedding 层的参数行为与非 Embedding 层不同,分析时应排除 Embedding 参数。
4. 批量大小 (Batch Size)
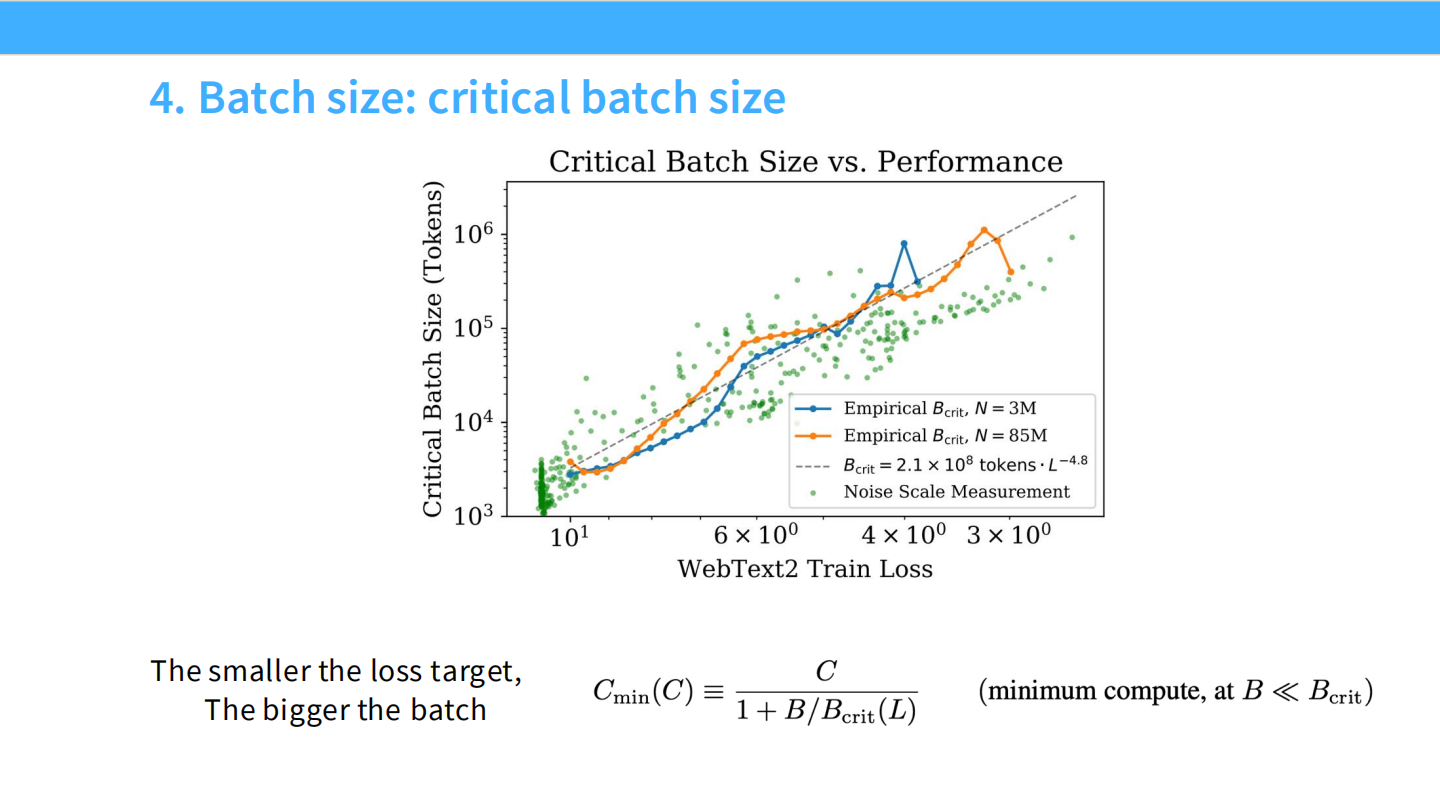
- **临界批量大小 ($B_{crit}$)**:达到目标 Loss 所需的最小样本数与最小步数之间的平衡点。
- 规律:目标 Loss 越小(模型越好),最优 Batch Size 越大 ($B_{crit} \approx L^{-4.8}$)。
- 结论:随着模型规模和算力增加,应该增大 Batch Size。这对数据并行有利。
5. 学习率 (Learning Rate)与 muP
- 问题:直接放大模型,最优 LR 会变,难以预测。
- **解决方案 (muP)**:Maximal Update Parametrization (Yang et al 2022)。通过特定的参数化,使得最优 LR 在不同模型规模间保持稳定,可以直接从小模型迁移到大模型。
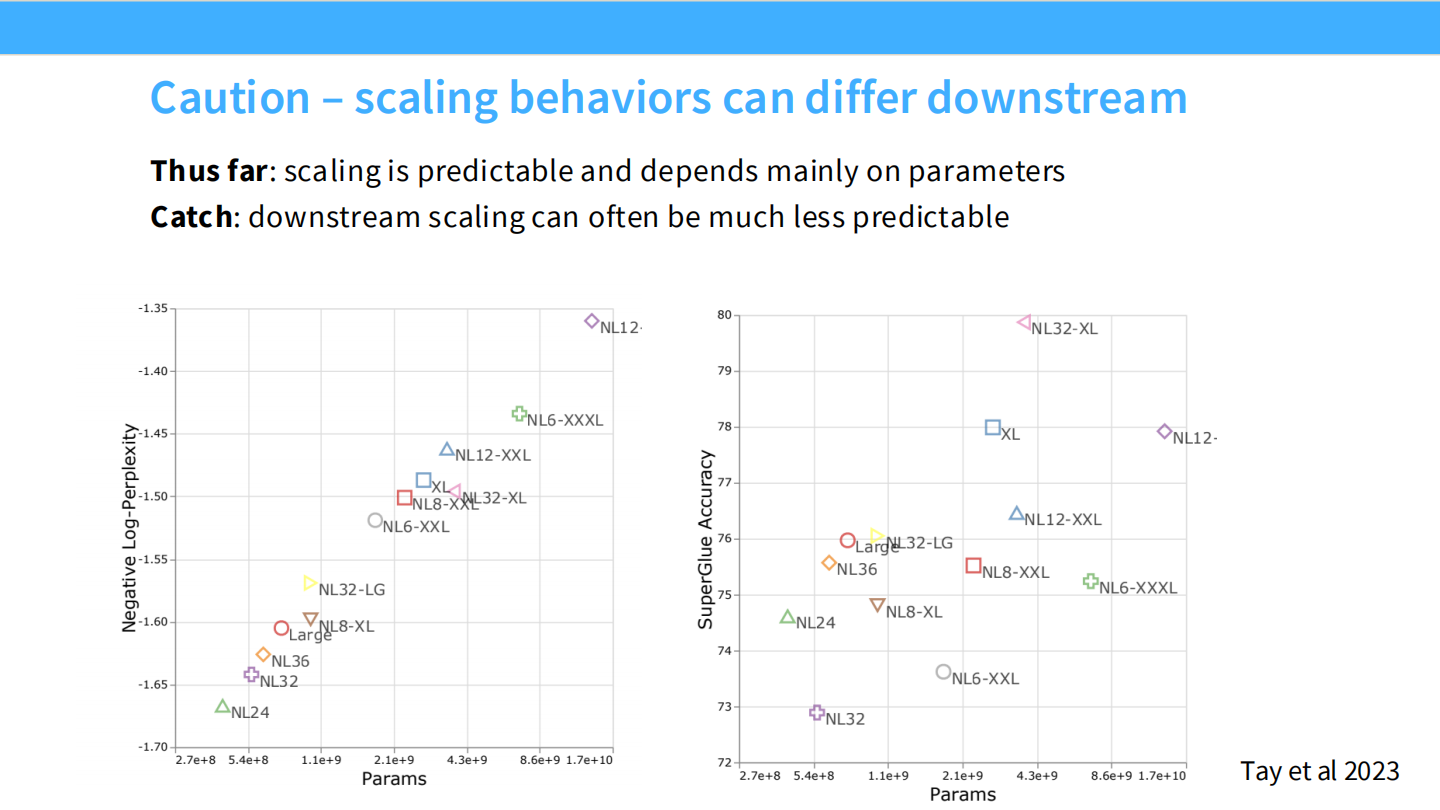
警告:以上讨论针对预训练 Loss。下游任务(如 SuperGlue)的 Scaling 行为可能不可预测(涌现、突变)。
Part 4. 算力权衡与 Chinchilla Scaling Laws
联合 Scaling Laws (Joint Scaling)
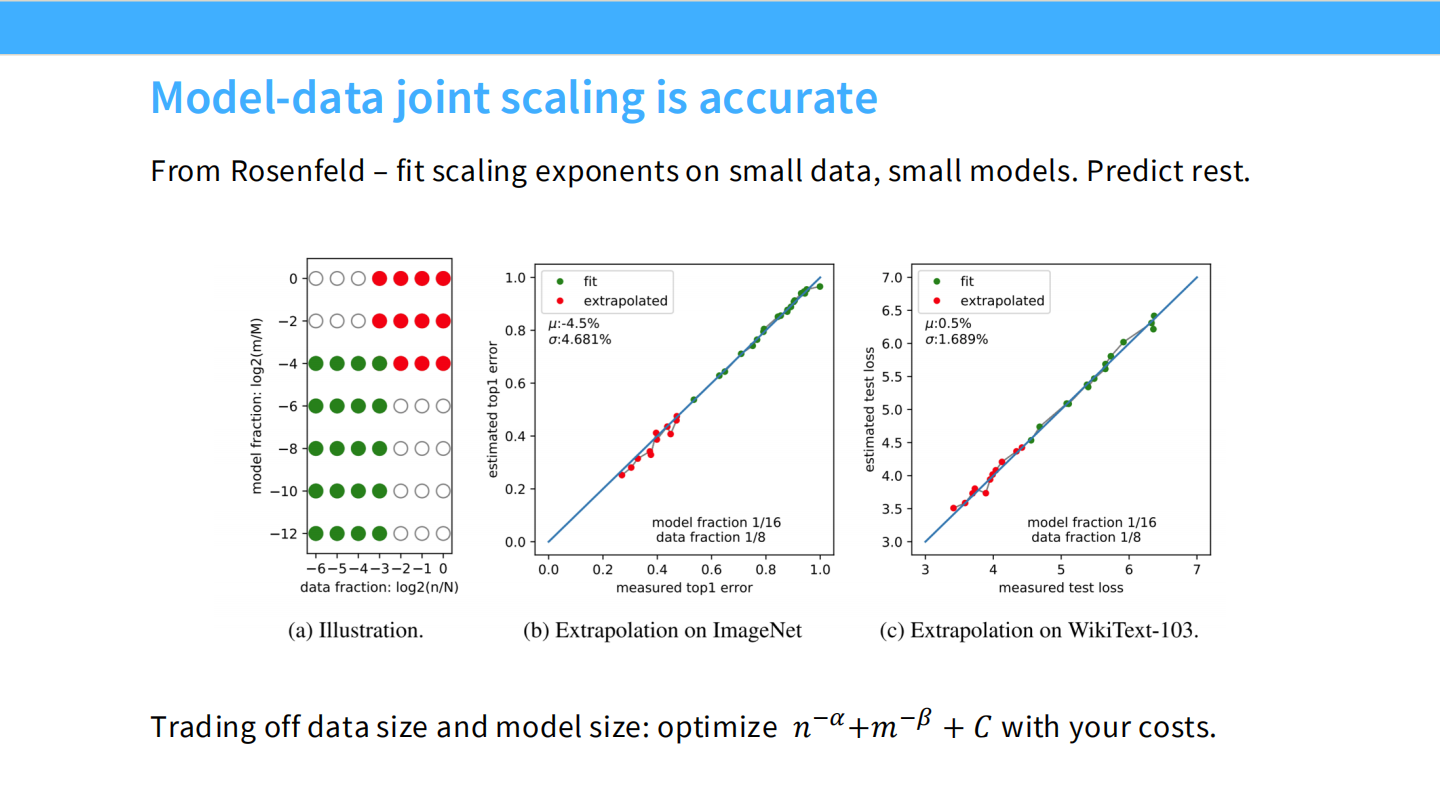
我们需要一个公式同时描述数据量 ($n$) 和模型大小 ($m$) 对误差的影响:
$$ Error = n^{-\alpha} + m^{-\beta} + C $$
或者 Kaplan 的形式:
$$ Error = [m^{-\alpha} + n^{-1}]^\beta $$
这允许我们在固定算力预算下进行权衡。
Kaplan vs. Chinchilla (The Great Debate)
1. Kaplan et al. (2020) 的结论
- 主张:模型参数量比数据量更重要。
- 建议:把算力主要花在把模型做大上,数据量不用增加太多。
2. Chinchilla (Hoffman et al. 2022) 的修正
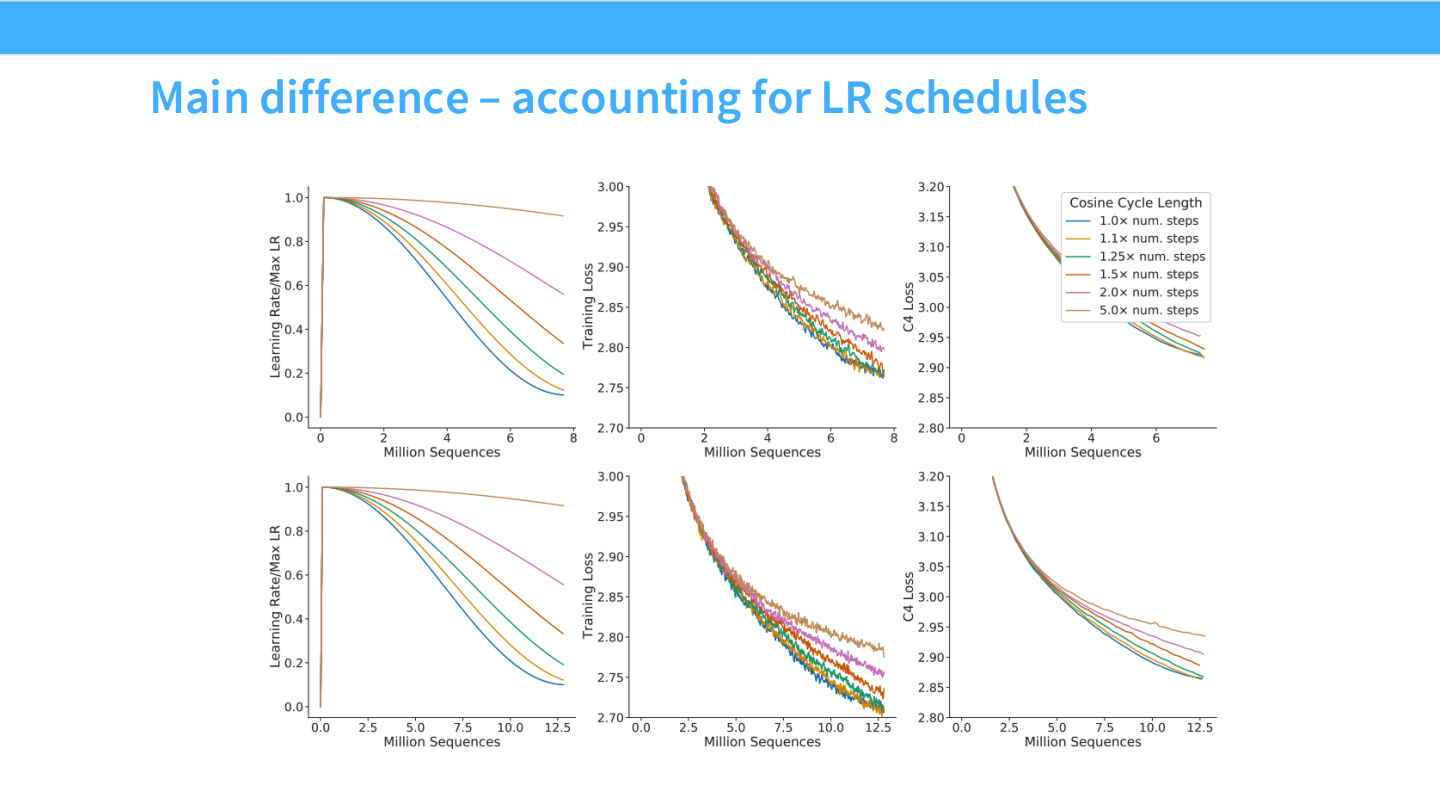
- 发现 Kaplan 的错误:Kaplan 在做实验时,没有根据训练步数正确调整**学习率调度 (LR Schedule / Cosine decay)**。
- Chinchilla 的方法:为每个训练时长专门调整 LR Schedule,重新拟合 Scaling Laws。
- Chinchilla 的结论:
- 模型大小和数据量应该等比例扩展 ($N \approx D$)。
- 即:算力增加 10 倍,模型参数量扩大 3.x 倍,数据量也扩大 3.x 倍。
Chinchilla 的拟合方法
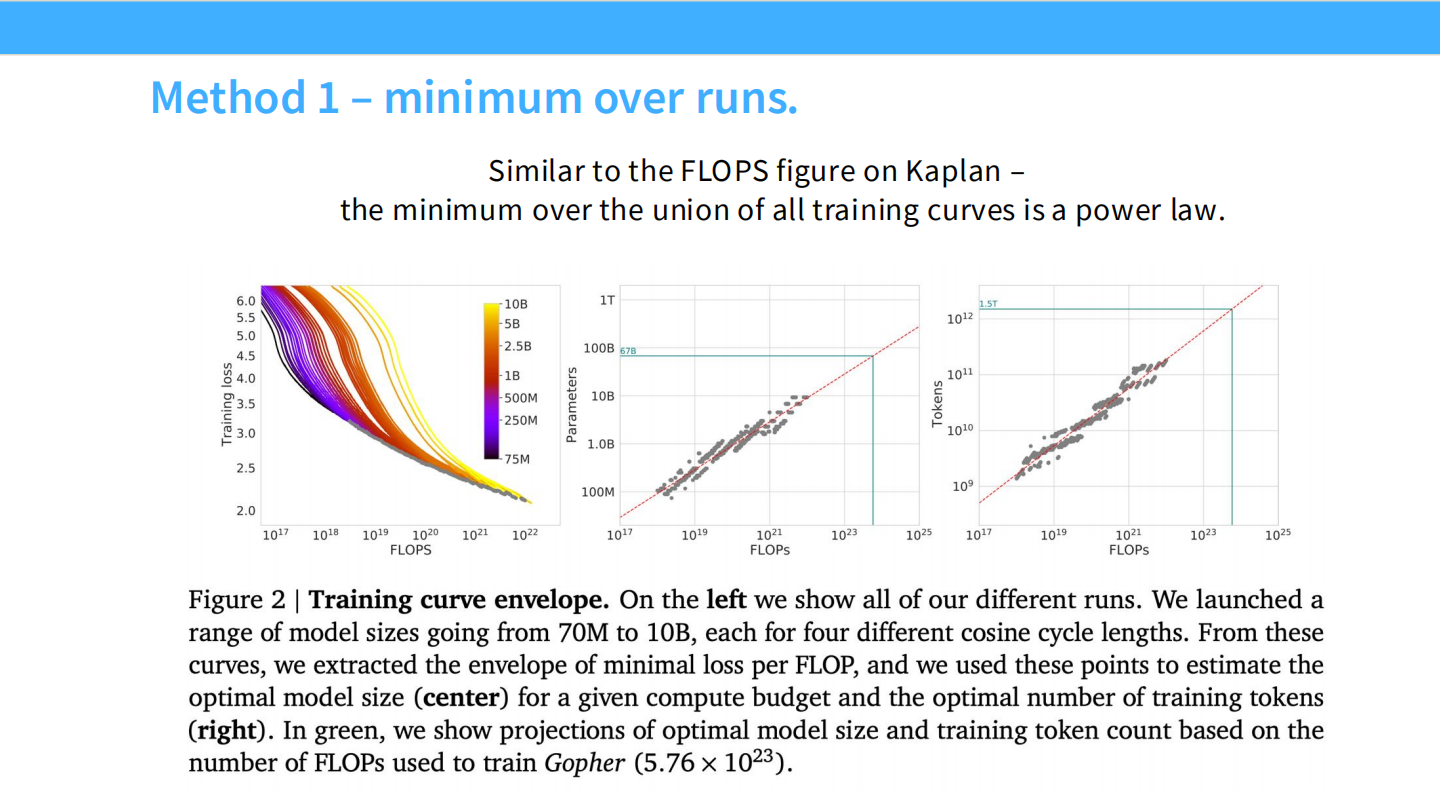
作者使用了三种方法,结果一致:
- Minimum over runs:画出不同模型的包络线。
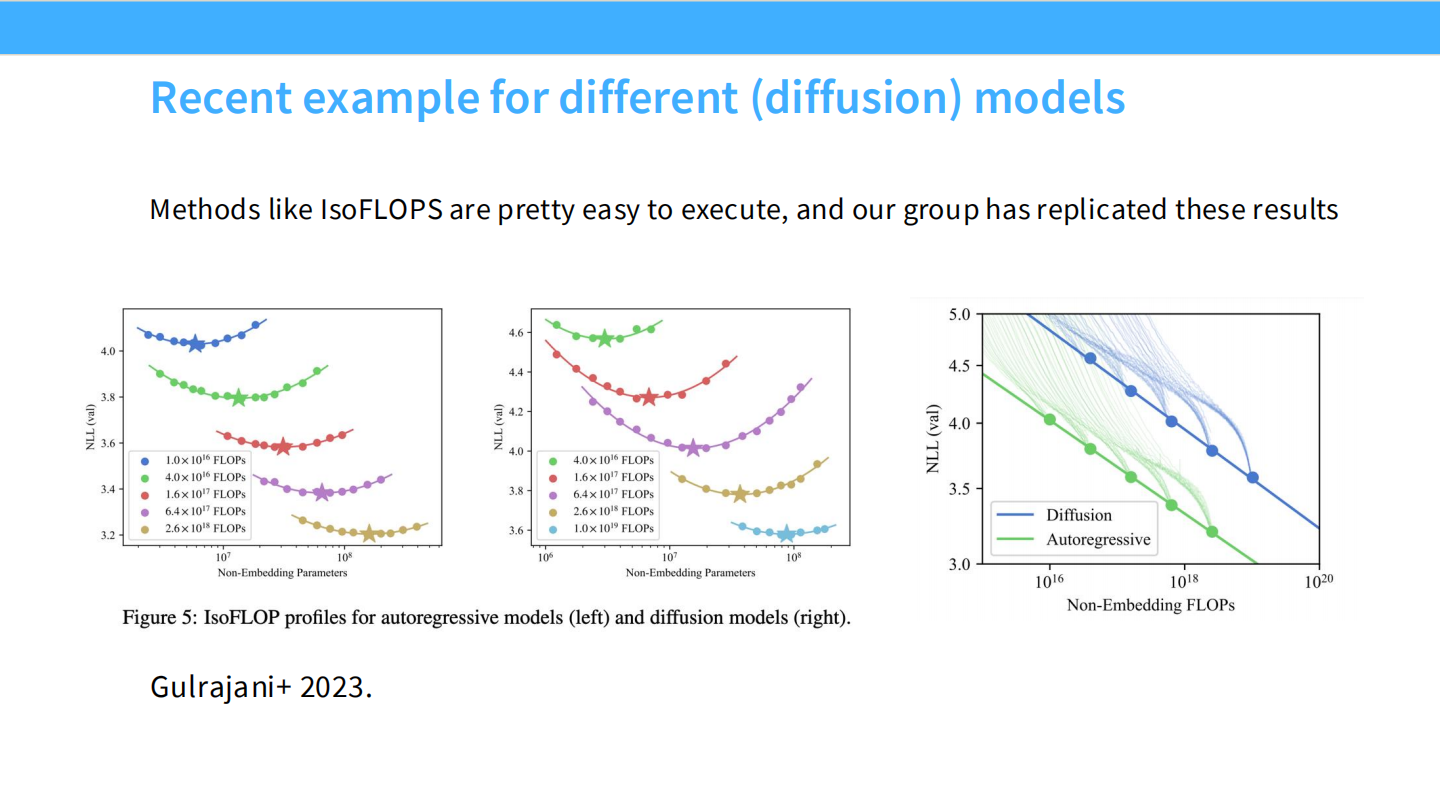
- IsoFLOPS:在固定算力预算下,寻找 Loss 最低的模型大小(呈现凸曲线)。
- Parametric Fit:联合参数拟合。
训练最优 vs. 推理最优 (Training vs. Inference Optimal)
Chinchilla 定律告诉你的是:固定训练算力下的最优模型。
但在实际应用中,推理成本 (Inference Cost) 往往更重要。
- Chinchilla 推荐:~20 tokens / param
- Llama 2 70B:~29 tokens / param
- Llama 3 70B:~215 tokens / param
结论:如果预期推理量很大,为了降低推理成本(模型越小推理越便宜),应该“过度训练” (Over-train) 小模型(使用远超 Chinchilla 推荐的数据量)。
总结

- Log-Linearity:对数线性关系延伸到了模型参数和计算量。
- 设计流程:
- 利用小模型设定:优化器、架构、模型尺寸。
- 根据 Scaling Law 进行预测。
- 权衡资源:根据你是追求“训练最优”(Chinchilla)还是“推理最优”(Llama),决定是把算力花在更大的模型上,还是更多的数据上。