大模型从0到1｜第四讲：详解MoE架构

课程信息： CS336 | 讲师： Tatsu H | 主题： 混合专家模型 (Mixture of Experts)

课程链接：Stanford CS336 Spring 2025 - Lecture 4: MoEs

---

Part 1: MoE 的背景与崛起 (Introduction & Context)

Page 1: 课程开篇

• 【视觉内容】 简洁的标题页。
• 【深度解析】 本节课是 CS336 系列课程的第四讲，核心议题是 **Mixtures of Experts (MoE)**。MoE 是当前大模型（LLM）领域从“稠密模型”向“稀疏模型”转型的关键技术，也是 GPT-4 等顶尖模型背后的核心架构。

Page 2: MoE 的统治地位

• 【视觉内容】
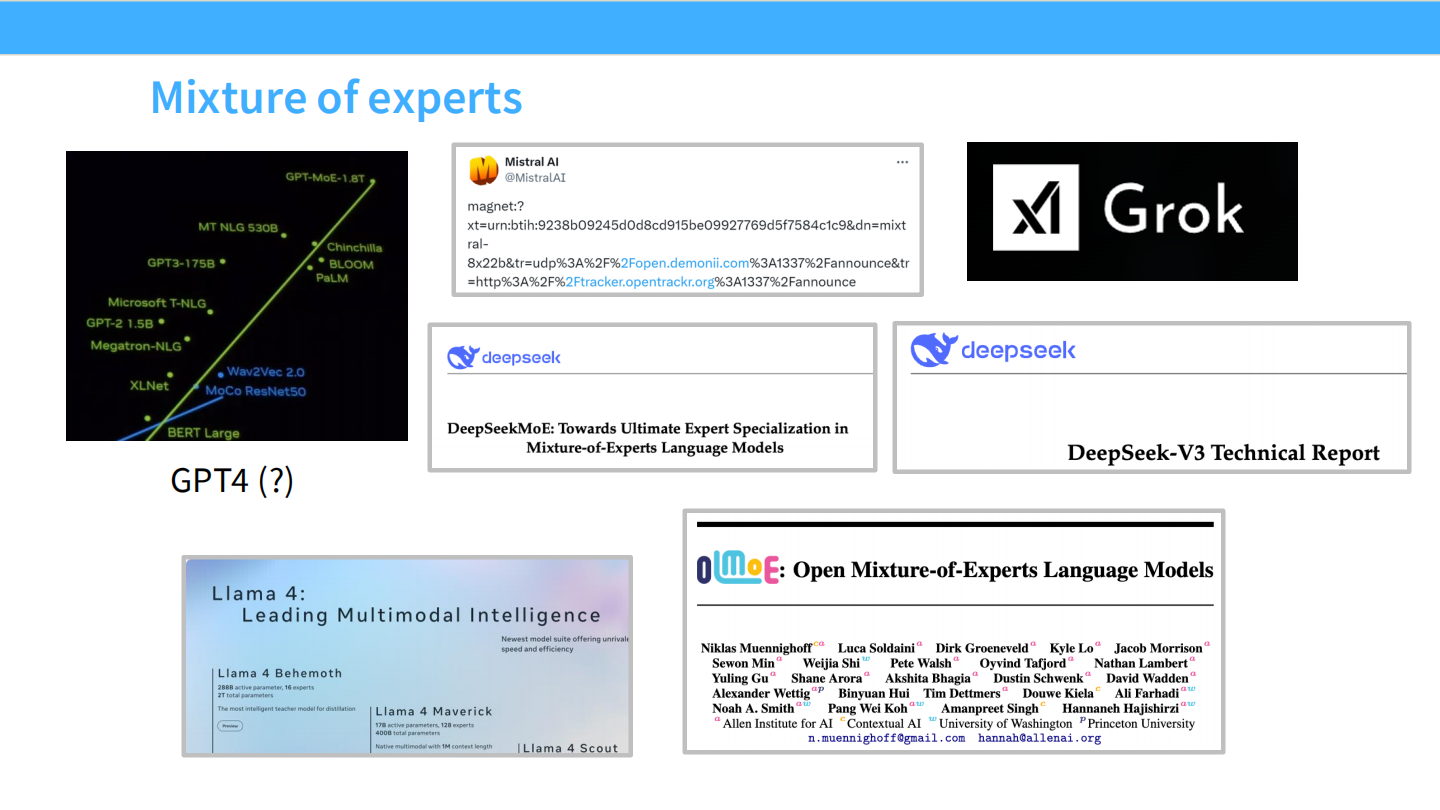
  • 左侧图表： 展示了模型参数量的指数级增长。图中绿色点列出了 GPT-2 (1.5B), GPT-3 (175B), MT NLG (530B)。最顶端黄色的点标注为 **”GPT-MoE-1.8T”**，暗示 GPT-4 是一个约 1.8 万亿参数的 MoE 模型。
  • 右侧情报： 拼贴了 Mistral AI（磁力链接泄露事件，代表 Mixtral 8x7B）、Grok（马斯克的 xAI 开源 MoE）、DeepSeek（深度求索的技术报告）以及 Llama 4（代号 Maverick/Behemoth）的相关信息。
• 【深度解析】
  • 现状： MoE 已经不再是“实验性”技术，而是成为了**行业标准 (Industry Standard)**。
  • 趋势： 无论是闭源霸主（GPT-4），还是开源先锋（Mixtral, DeepSeek），甚至是未来的 Llama 4，都在拥抱 MoE 架构。这标志着大模型进入了“稀疏计算”时代。

Page 3: MoE 的本质 (What is a MoE?)

• 【视觉内容】 架构对比图。
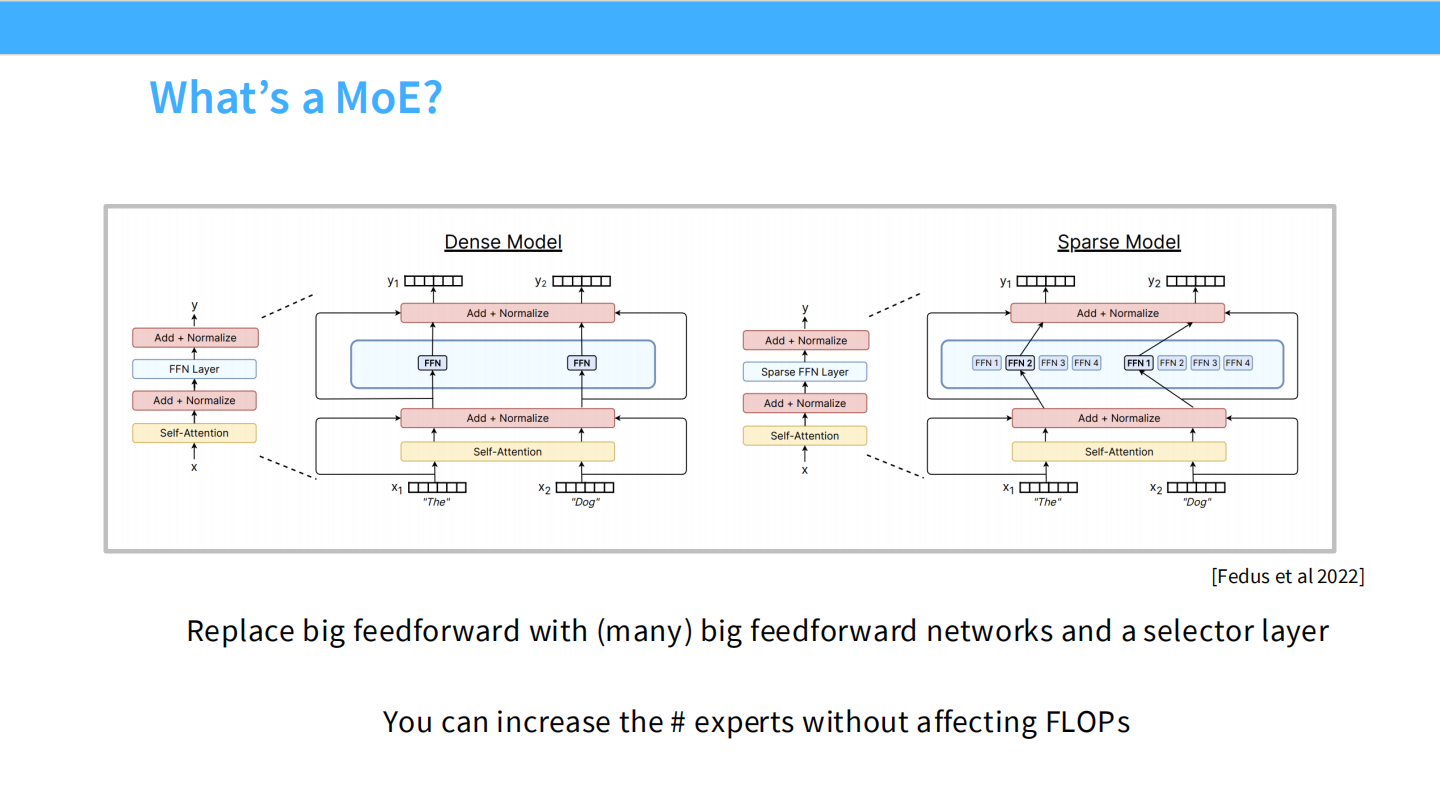
  • 左图 (Dense Model): 传统的 Transformer Block。输入向量 $x$ 经过 Layer Norm 后，进入一个巨大的 FFN (Feed Forward Network) 层，所有参数参与计算。
  • 右图 (Sparse Model): MoE Block。原本的大 FFN 被替换为一组**专家 (Experts)**，标记为 FFN 1 到 FFN 4。
  • 关键组件： **Router (选择器)**。它动态决定输入 $x$ 应该走哪条路（例如图中选了 FFN 2 和 FFN 4）。
• 【深度解析】
  • 核心定义： MoE 的本质是将大模型拆解。用许多个（Many）前馈网络替代一个大前馈网络，并引入一个**选择层 (Selector Layer)**。
  • 稀疏性 (Sparsity)： 对于每一个 Token，模型只激活一小部分参数（例如总共有 1000 亿参数，但处理一个词只用 100 亿）。
  • 铁律： **”You can increase the # experts without affecting FLOPs”**。这意味着你可以无限增加模型的总参数量（知识容量），而不增加推理时的计算量（延迟/成本）。

Page 4: Scaling Laws - 为什么 MoE 会赢？

• 【视觉内容】
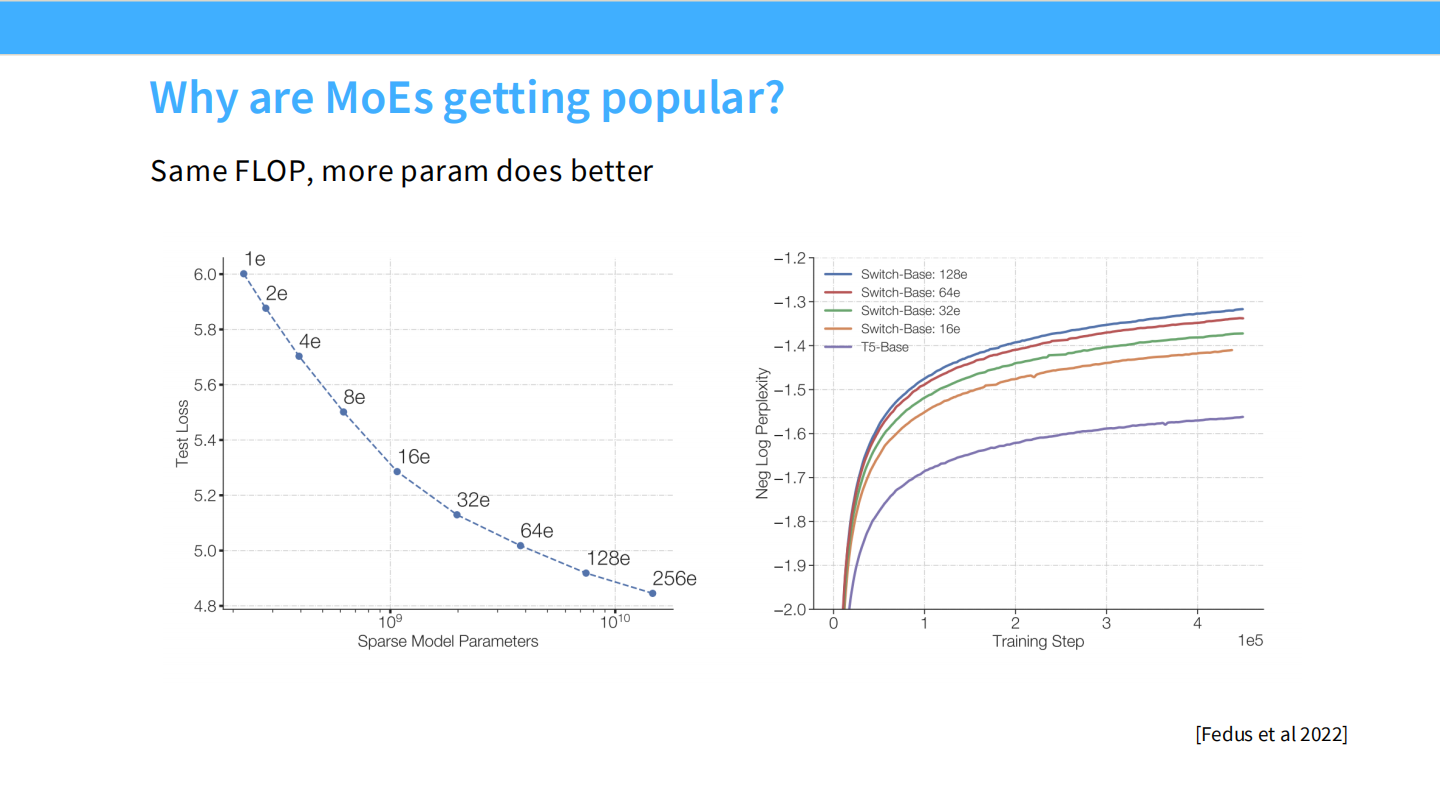
  • 左图： 横轴是稀疏模型参数量 ($10^9$ 到 $10^{10}$)，纵轴是 Test Loss。曲线上的点（4e, 8e, …, 256e）代表专家数量。可以看到，专家越多，Loss 越低，且没有饱和迹象。
  • 右图： 训练步数 vs Perplexity (困惑度)。Switch-Base-128e（蓝色最下方的线）的收敛效果远好于同计算量的稠密模型 T5-Base（紫色最上方的线）。
• 【深度解析】
  • Scaling Law： 在相同的计算预算 (Same FLOPs) 下，MoE 模型因为拥有更多的参数（尽管每次只用一部分），其性能（Loss）显著优于稠密模型。
  • 结论： “Same FLOP, more param does better.” 这打破了以往参数量与计算量必须同步增长的限制。

Page 5: 训练速度 - 巨大的效率提升

• 【视觉内容】
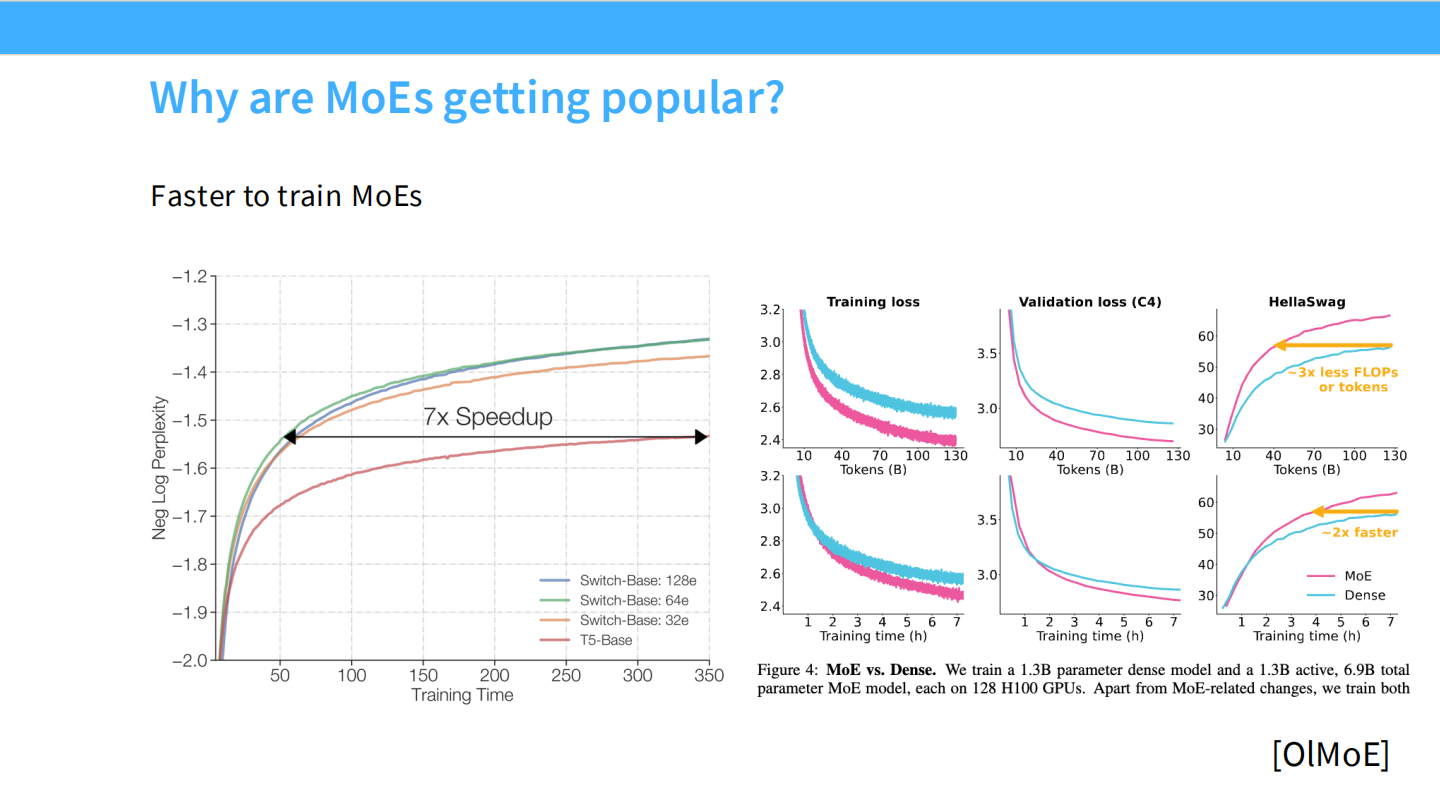
  • 左图： 横轴是训练时间，纵轴是 Log Perplexity。黑色双向箭头标出了 **”7x Speedup”**。MoE 模型达到某个 Loss 值的时间仅为 Dense 模型的 1/7。
  • 右图： 引用 OlMoE 的数据。粉色线 (MoE) 的下降斜率远超蓝色线 (Dense)。标注显示 “~2x faster” (更少 FLOPs 或 tokens 达到同等精度)。
• 【深度解析】
  • 效率优势： 训练 MoE 不仅最终效果好，过程也更快。因为每次反向传播只更新被激活的那一小部分专家的权重，模型能以更少的计算资源“见过”更多的数据模式。
  • 经济性： 对于想要快速迭代模型的公司来说，MoE 是节省 GPU 机时的首选。

Page 6: 性能竞争力 - 越级挑战

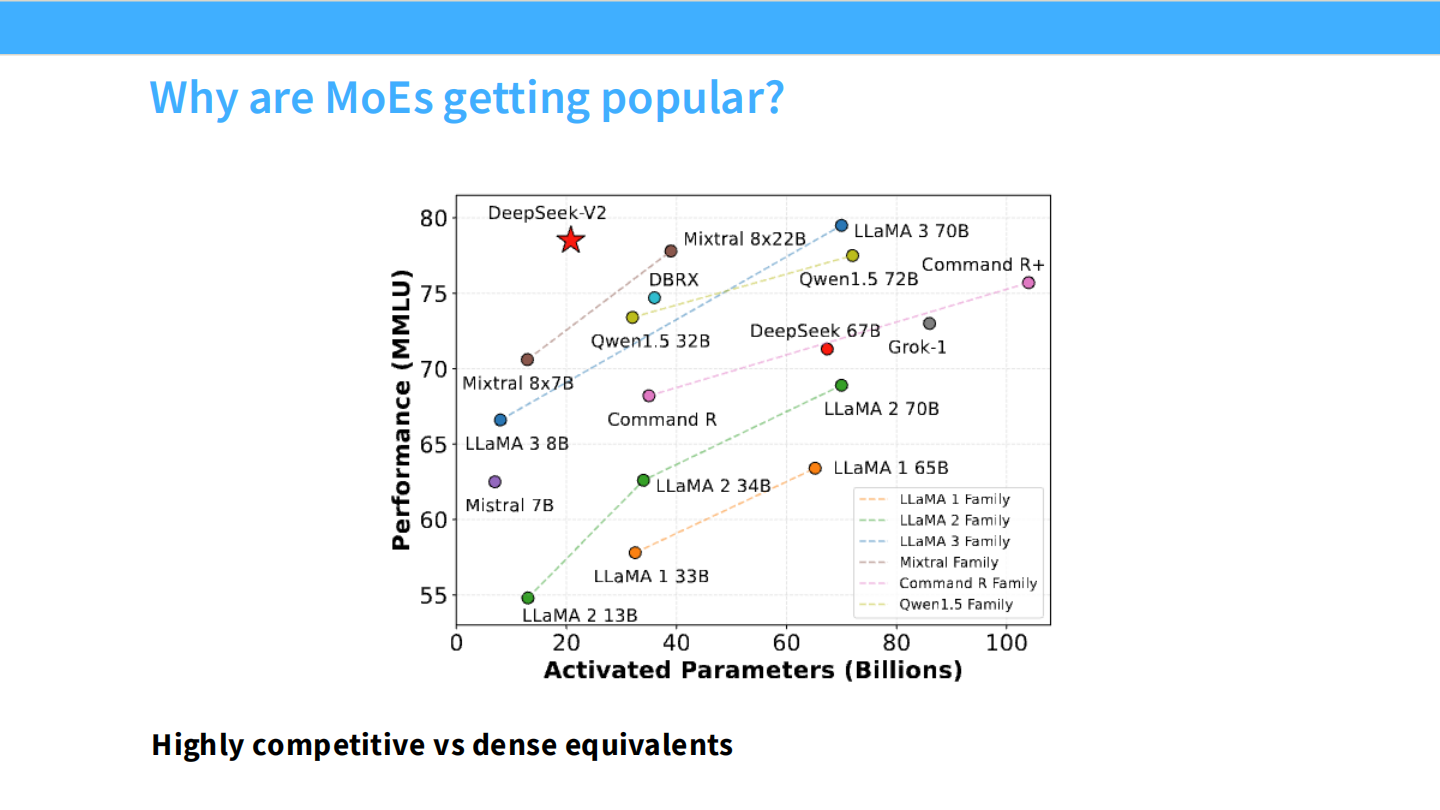
• 【视觉内容】 散点图。横轴是 **”Activated Parameters” (激活参数量)**，纵轴是 **”Performance (MMLU)”**。
  • 关键对比： 注意红色的五角星 DeepSeek-V2。它的激活参数量非常小（约 20B+），但 MMLU 得分却高达 80 左右，超过了 LLaMA 3 70B（稠密模型，激活参数 70B）和 Mixtral 8x22B。
• 【深度解析】
  • 核心竞争力： MoE 的魔力在于“以小博大”。看推理成本（激活参数），它是一个小模型；看智能水平（MMLU），它是一个大模型。
  • 图表证明了 MoE 相比同等级别的 Dense 模型具有显著的性能优势（Highly competitive）。

Page 7: 系统架构 - 天生的并行性

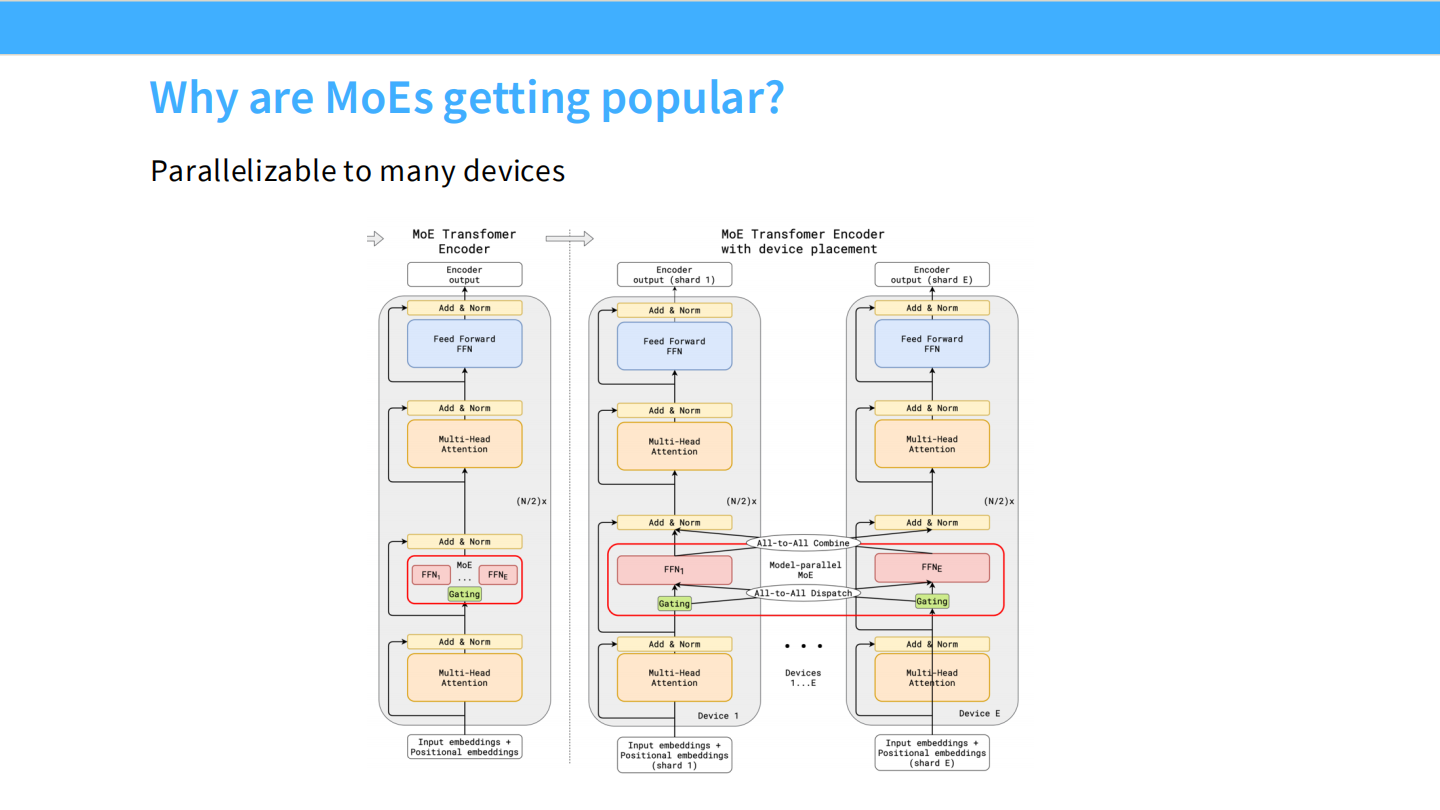
• 【视觉内容】 复杂的 Transformer Encoder 流程图。
  • 左侧是逻辑视图，右侧是物理视图（With device placement）。
  • 关键路径： Encoder Output -> Add & Norm -> Feed Forward FFN。
  • 在 FFN 处，数据流被分发 (Dispatch) 到了 Devices 1…E。这意味着 FFN1 在显卡 1 上，FFN2 在显卡 2 上……计算完后再合并 (Combine)。
• 【深度解析】
  • 并行化 (Parallelizable)： MoE 架构非常适合分布式训练。每个 Expert 可以被视为一个独立的计算单元，完美契合多 GPU 集群。
  • 这种并行模式被称为 **Expert Parallelism (EP)**，是 MoE 能够扩展到万亿参数的基石。

Page 8: 东西方对决 - 开源 MoE 的胜利

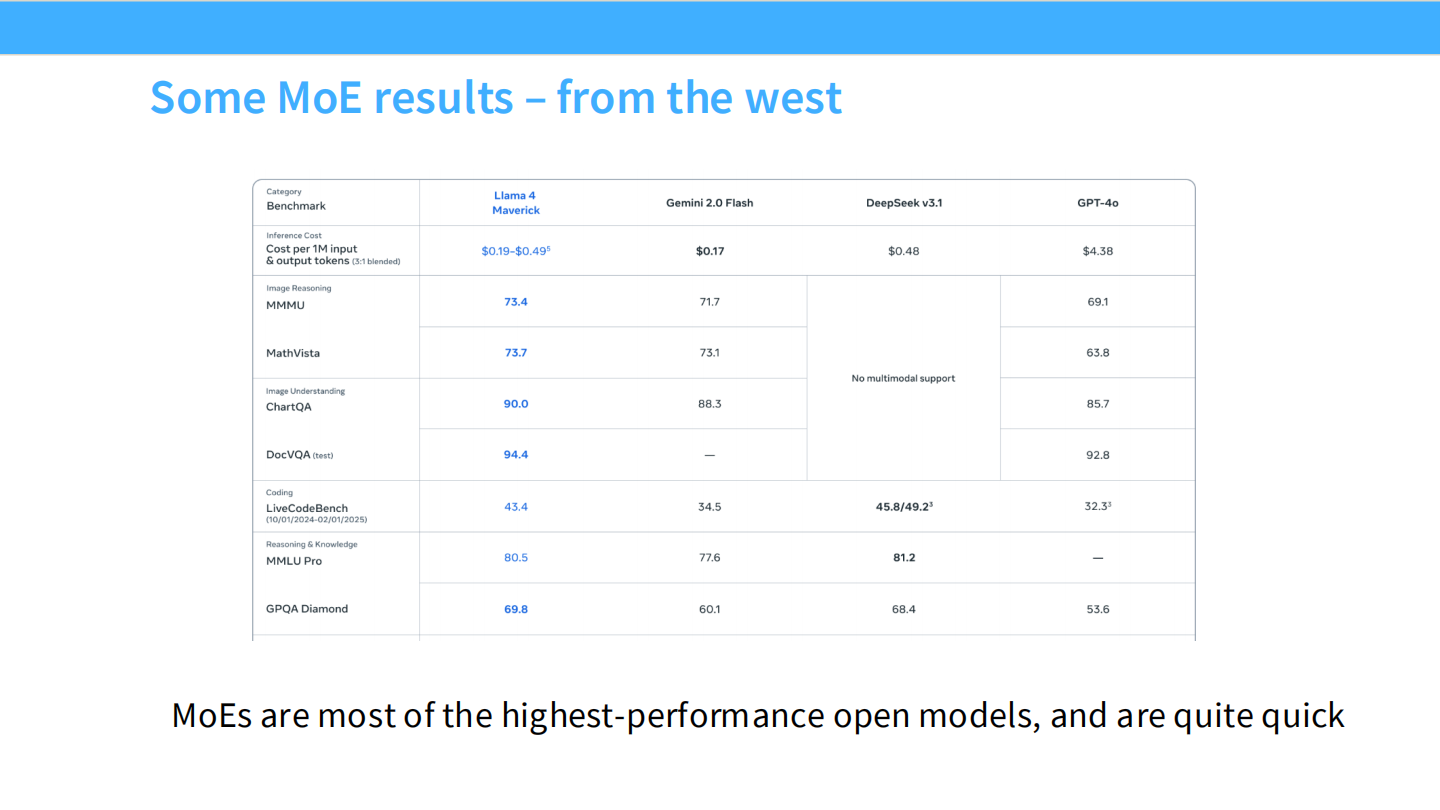
• 【视觉内容】 详细的数据表格，对比了 Llama 4 (Maverick), Gemini 2.0 Flash, DeepSeek v3.1, GPT-4o。
  • 成本对比： DeepSeek v3.1 的每百万输入 Token 成本仅为 $0.14 (此处 PPT 可能写错，DeepSeek 官方更低，图中显示推理成本比 GPT-4o 的 $4.38 低一个数量级)。
  • 能力对比： 在数学推理 (MathVista) 上，DeepSeek (63.8) 和 GPT-4o (63.8) 持平，Llama 4 (73.7) 表现强劲。
• 【深度解析】
  • 市场格局： MoE 已经成为高性能开源模型（如 DeepSeek, Mixtral）的首选架构。
  • 优势： “Quite quick” —— 它们不仅强，而且快。DeepSeek V3 证明了极致优化的 MoE 可以比闭源模型便宜非常多。

Page 9: 中国早期探索 - 小参数 MoE (Qwen)

• 【视觉内容】
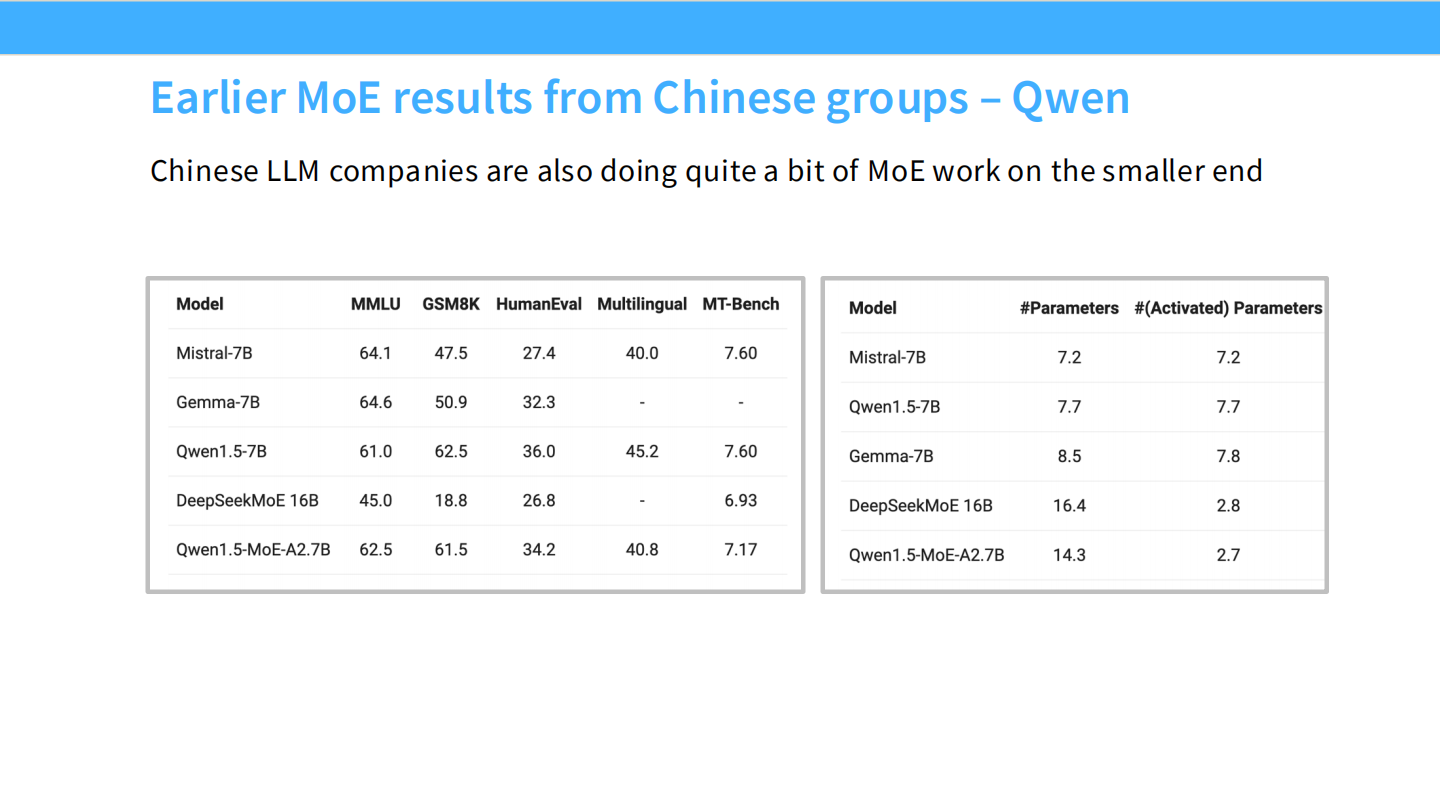
  • 左表 (跑分)： 对比了 Mistral-7B, Gemma-7B, Qwen1.5-7B 以及 Qwen1.5-MoE-A2.7B。注意 Qwen1.5-MoE 的 MMLU (62.5) 接近 Mistral-7B (64.1)，但其激活参数要小得多。
  • 右表 (参数)： Qwen1.5-MoE-A2.7B 的总参数是 14.3B，但 #Activated Parameters 仅为 2.7B。DeepSeekMoE 16B 的激活参数仅为 2.8B。
• 【深度解析】
  • 不同的路： 早期中国大模型团队（如 Qwen, DeepSeek）并没有一上来就做万亿 MoE，而是在小规模 (Smaller end) 上进行了大量实验。
  • 极致效率： 他们证明了用 2.7B 的计算量（相当于在手机上能跑的大小）可以达到 7B 甚至更大的模型效果。

Page 10: DeepSeek 的早期消融实验

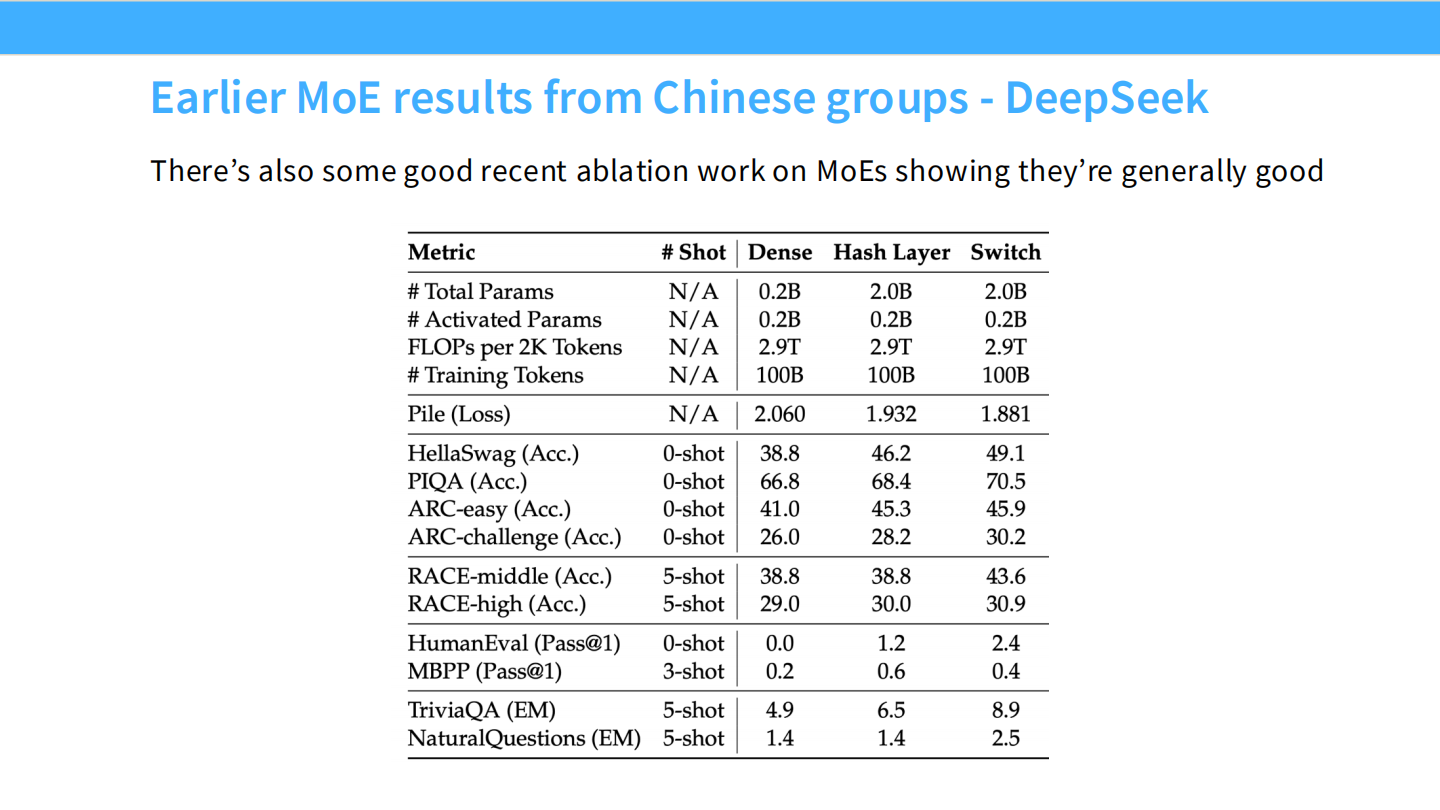
• 【视觉内容】 这是一个非常学术的表格，对比了三种架构：Dense (0.2B) vs Hash Layer (2.0B) vs **Switch (2.0B)**。
  • Hash Layer 和 Switch 都是 MoE 的变体，总参数量扩大了 10 倍（0.2B -> 2.0B），但激活参数量保持 0.2B 不变。
  • 结果： Switch 架构的 Pile (Loss) 从 2.060 降到了 1.881；HellaSwag 准确率从 38.8 飙升到 49.1。
• 【深度解析】
  • 结论： 即使是早期的实验也表明，**”They’re generally good”**。只要把 Dense 层换成 MoE 层，在计算量不变的情况下，模型性能就会全面提升。这为后续大规模投入 MoE 提供了理论信心。

Page 11: DeepSeek V3 - 新王登基

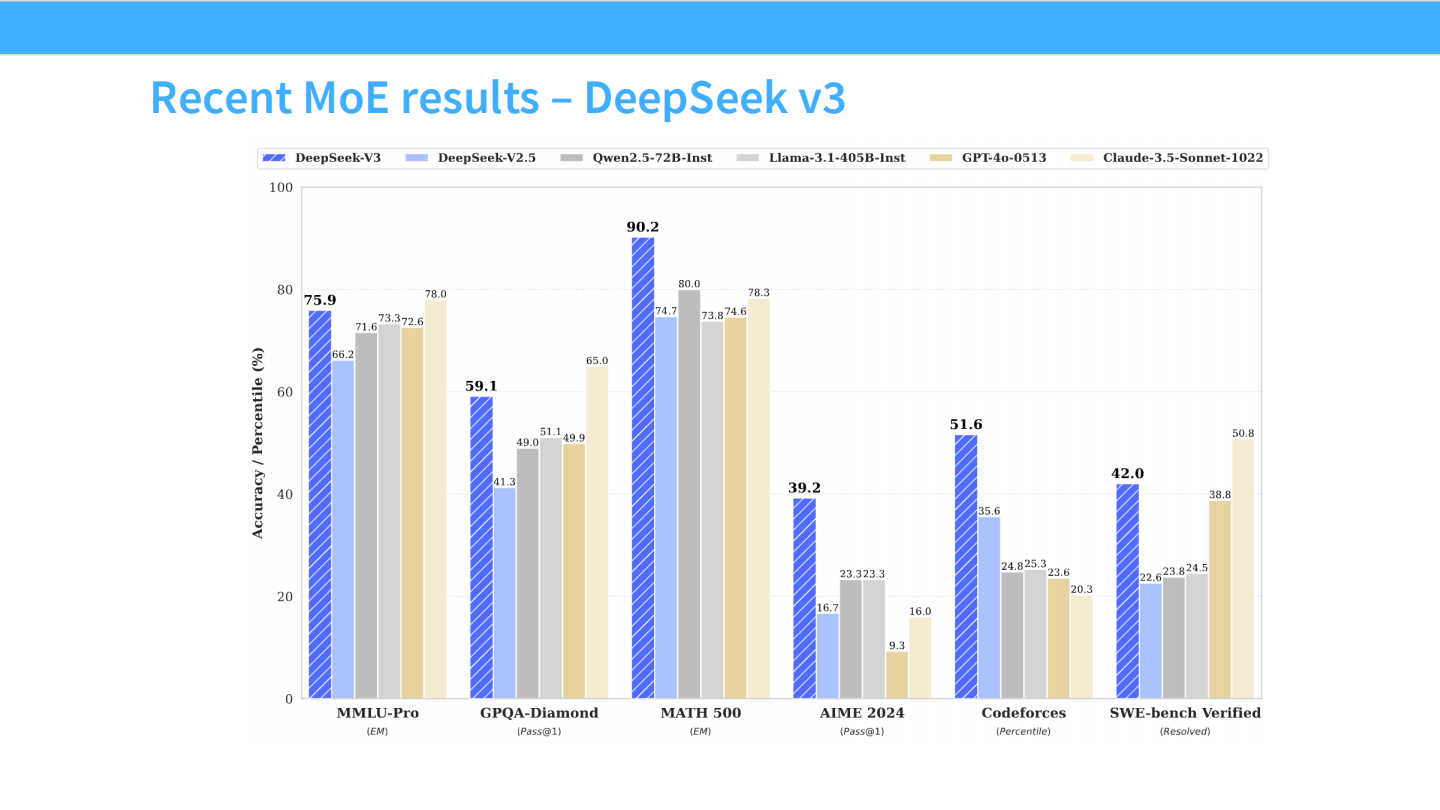
• 【视觉内容】 柱状图展示了 DeepSeek-V3 (深蓝色柱子) 在各项基准测试上的表现。
  • MATH 500: DeepSeek-V3 达到 90.2 分，远超 GPT-4o-0513 (73.8) 和 Claude-3.5-Sonnet (78.3)。
  • Codeforces: 也是大幅领先。
• 【深度解析】
  • SOTA 性能： DeepSeek V3 的发布是一个里程碑，证明了开源 MoE 模型可以在数学、代码等最考验逻辑推理的任务上，击败最强的闭源模型。

Page 12: MoE 的阴暗面 - 为什么难做？

• 【视觉内容】
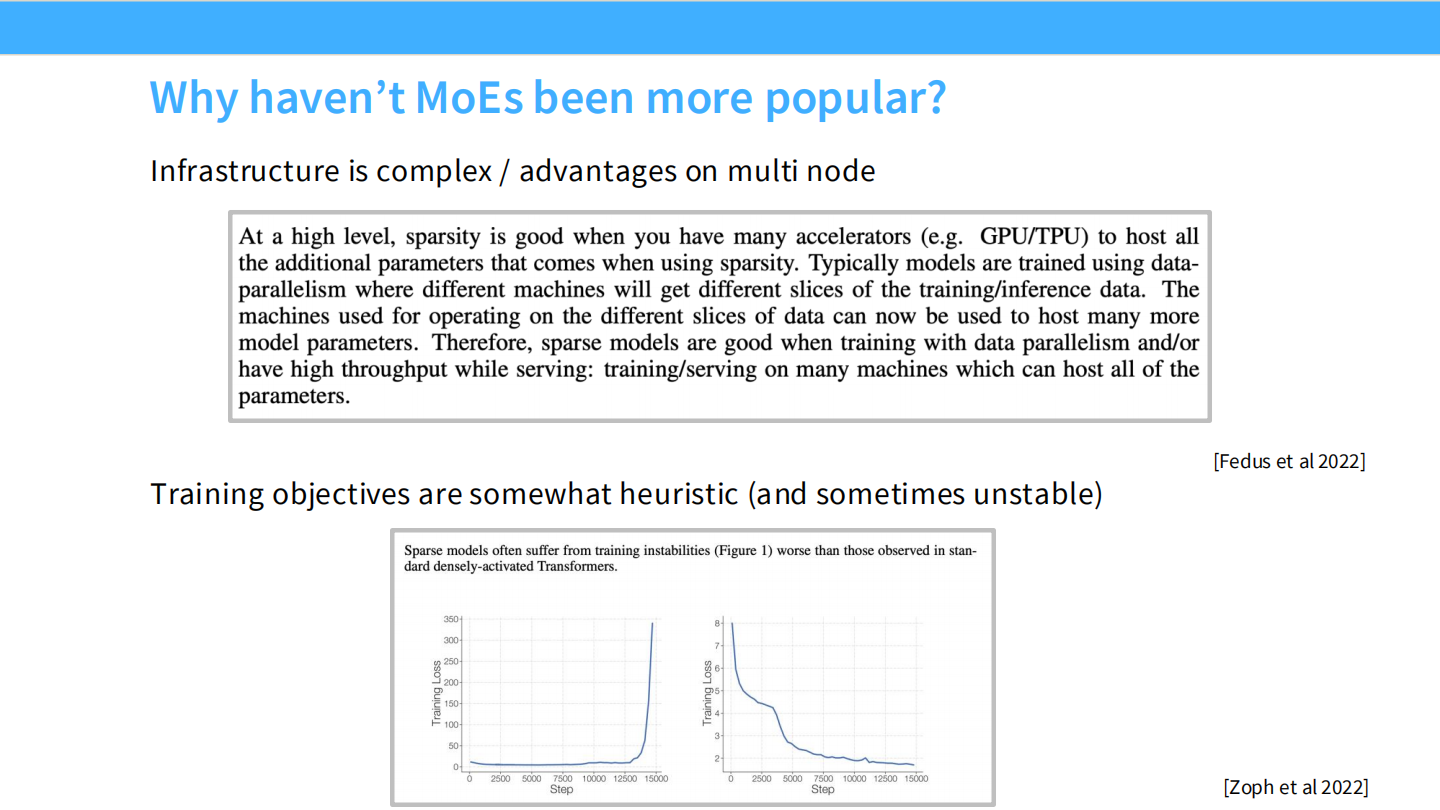
  • 上图（文本）： 摘录解释了稀疏性带来的基础设施挑战（需要 host many parameters, data parallelism, different machines…）。
  • 下图（曲线）： 展示了一次失败的训练。Loss 曲线在原本平滑下降的过程中，突然出现了一个巨大的 **Spike (尖刺)**，导致 Loss 暴涨，模型无法收敛。
• 【深度解析】
  • 两大拦路虎：
    1. 基建复杂 (Infrastructure)： 相比 Dense 模型，MoE 需要极其复杂的分布式系统支持，涉及跨节点的通信和显存管理。
    2. 训练不稳定 (Instability)： 训练目标通常包含启发式的 Loss，这导致模型极其脆弱，容易出现 Loss 爆炸。这是劝退很多团队的主要原因。

---

Part 2: 架构详解与路由机制 (Architecture Detail)

Page 13: MoE 到底长什么样？

• 【视觉内容】
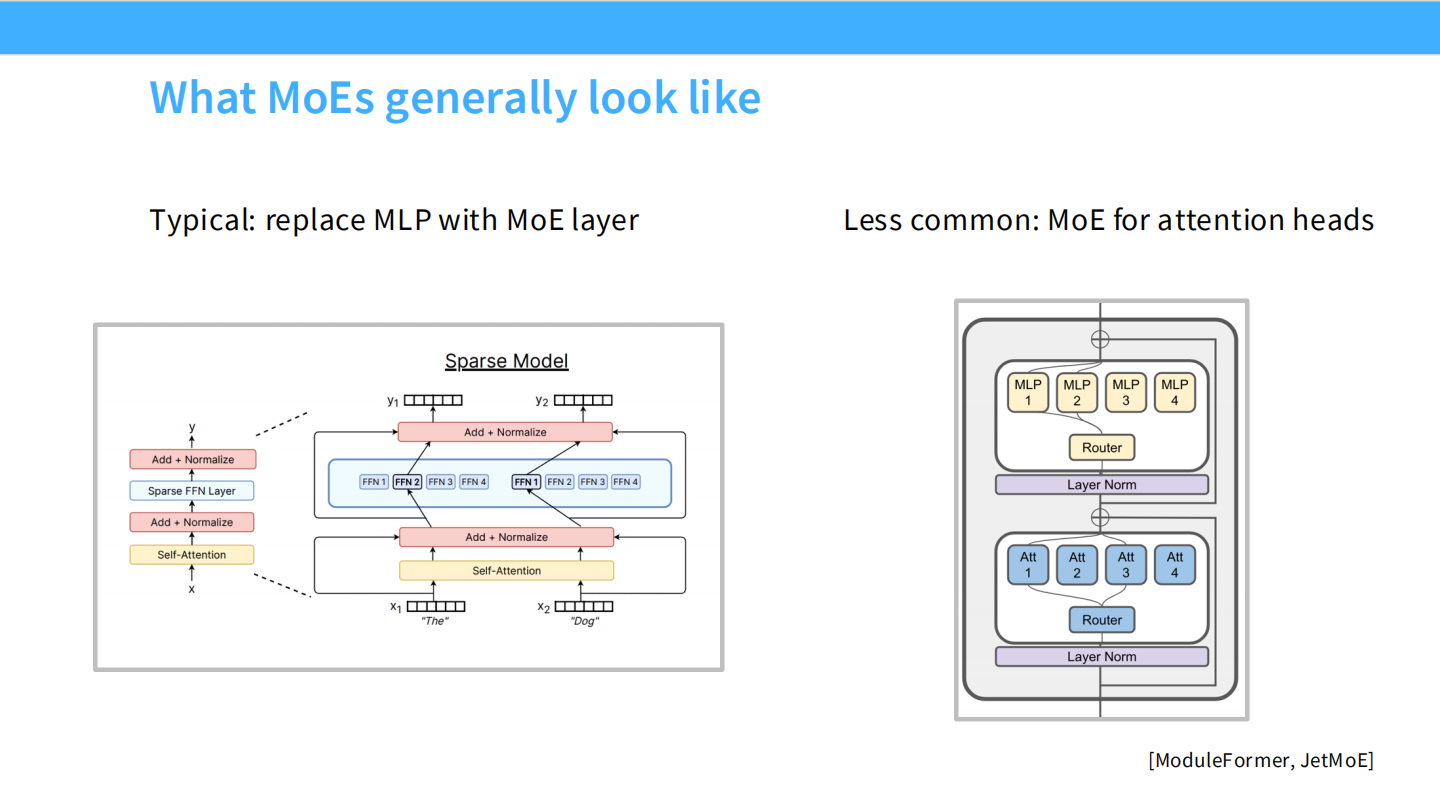
  • 左图 (Typical): 经典的 MoE 结构。Transformer Block 中的 Self-Attention 层保持不变，仅将 MLP (FFN) 层 替换为稀疏的专家层。
  • 右图 (Less common): 引用了 [ModuleFormer, JetMoE]。这种架构试图把 Attention 层也做成 MoE（每个 Head 也是专家），但这并不常见。
• 【深度解析】
  • 工业界标准： 目前几乎所有主流 MoE（GPT-4, Mixtral, DeepSeek）都采用左图方案。只动 FFN，不动 Attention。因为 FFN 占据了模型 2/3 的参数量，改动它收益最大。

Page 14: MoE 的三大变量

• 【视觉内容】 列表页。
• 【深度解析】 当我们设计一个 MoE 时，主要调整这三个参数：
  1. Routing function (路由函数)： 怎么选专家？（Top-k, Hash, RL…）
  2. Expert sizes (专家规模)： 专家是做大做少（Mixtral: 8个大专家），还是做小做多（DeepSeek: 256个小专家）？
  3. Training objectives (训练目标)： 除了语言模型的 Cross-Entropy Loss，还需要加什么辅助 Loss 来保证负载均衡？

Page 15: 路由算法概览

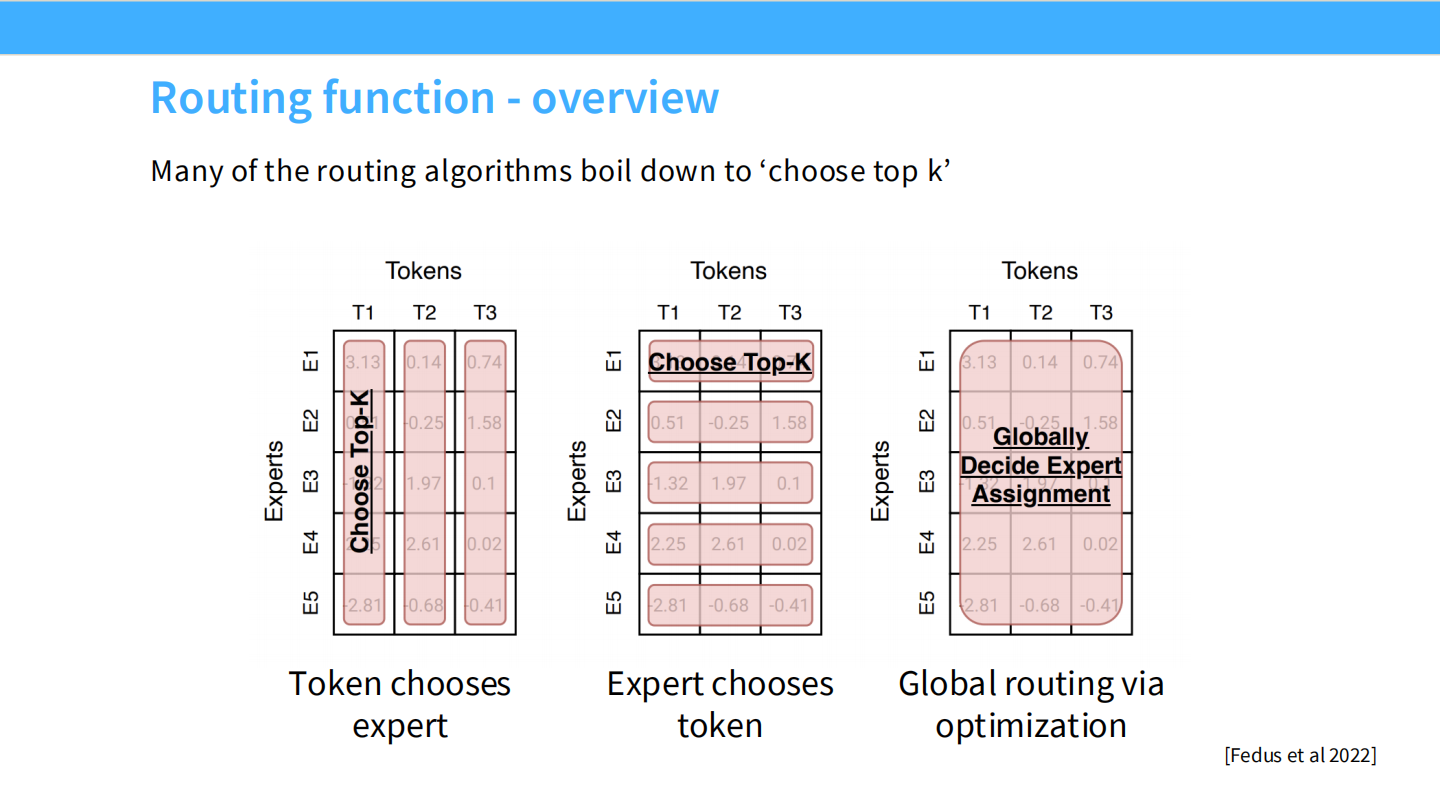
• 【视觉内容】 三个矩阵示意图，展示了 Token (行) 和 Expert (列) 的匹配逻辑。
  • 左图 (Token chooses expert): 每一行（Token）选择权重最高的 Top-K 列（Expert）。这是 Standard Top-K。
  • 中图 (Expert chooses token): 每一列（Expert）选择权重最高的 Top-K 行（Token）。这叫 Expert Choice。
  • 右图 (Global routing): 通过线性规划进行全局最优匹配。
• 【深度解析】
  • 现状： 尽管学术界提出了很多花哨的方法，但工业界最终收敛到了最简单粗暴的 **”Choose Top-K” (左图)**。

Page 16: 路由类型消融实验

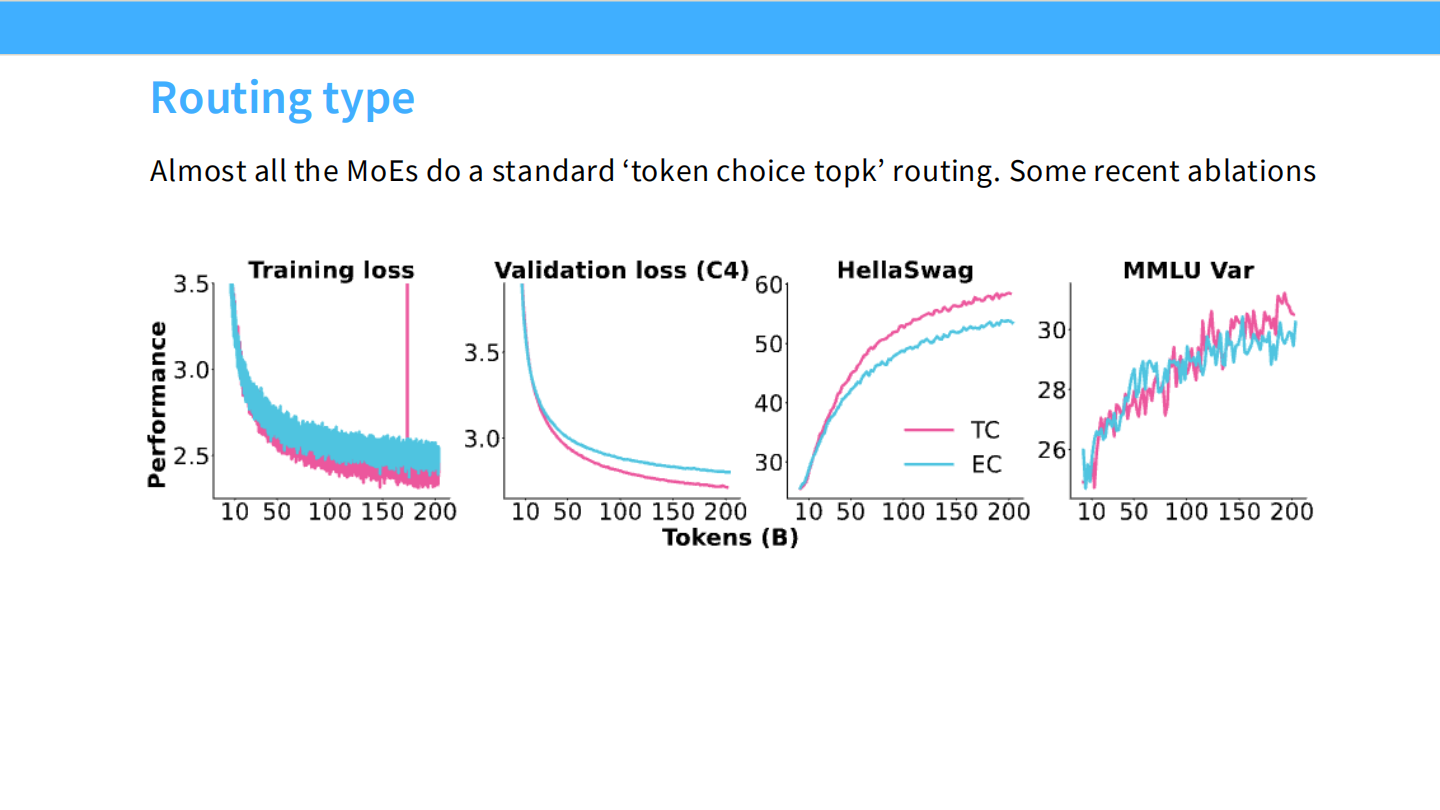
• 【视觉内容】 曲线图对比。
  • 粉色线 (TC - Token Choice): 标准 Top-k。
  • 蓝色线 (EC - Expert Choice): 专家选 Token。
  • 结果： 在 Training loss, Validation loss, HellaSwag, MMLU 等所有指标上，两条线几乎完全重合。
• 【深度解析】
  • 结论： “Almost all the MoEs do a standard token choice topk routing.” 既然复杂的 Expert Choice 并没有带来性能提升，大家自然选择实现更简单的 Top-k。

Page 17: 主流路由变体详解

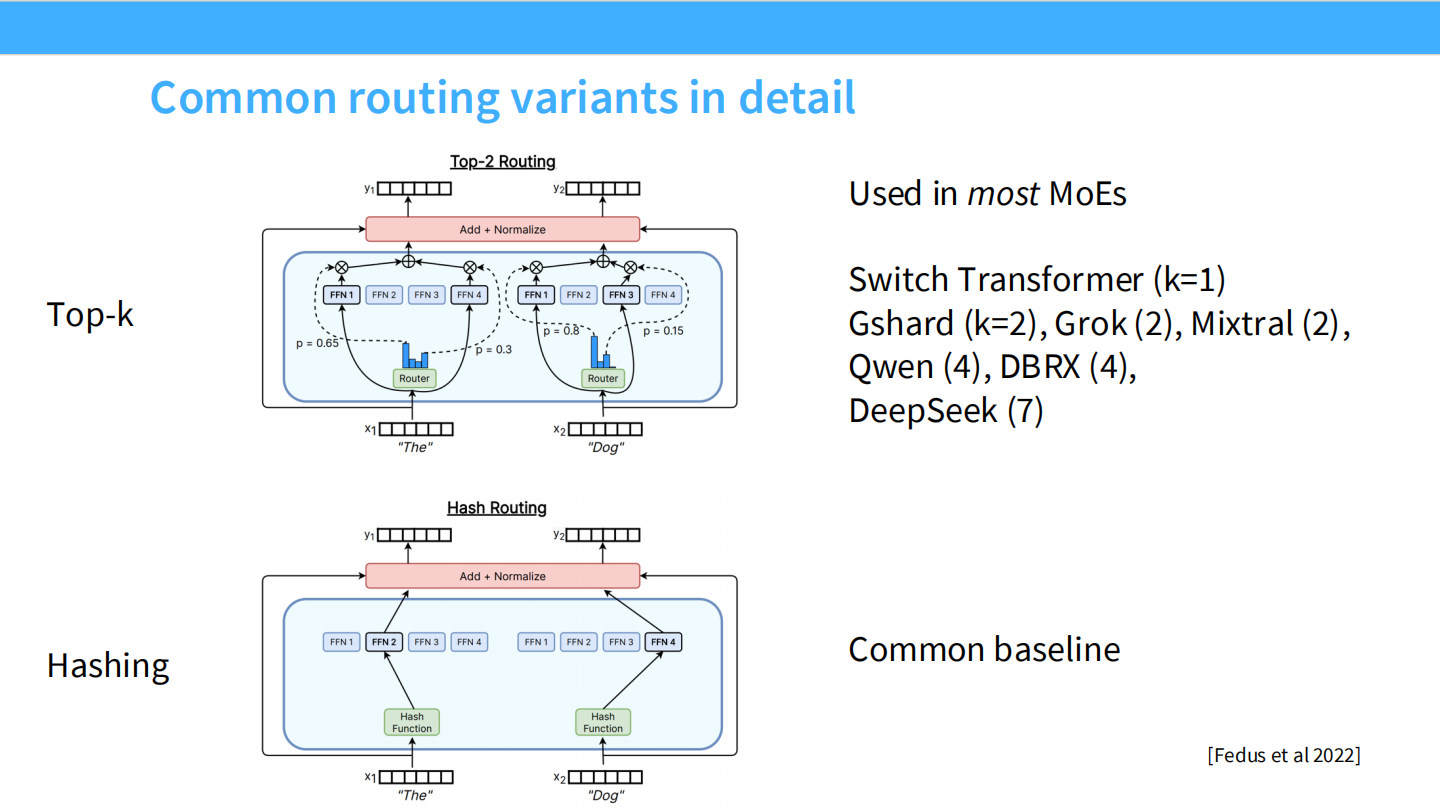
• 【视觉内容】
  • Top-k (上图): 展示了带有 Router 和 Softmax 的结构。
    • Switch Transformer: k=1 (单专家)。
    • Gshard, Grok, Mixtral: k=2。
    • Qwen, DBRX: k=4。
    • DeepSeek: k=8 (这里PPT写了7，实际上 V3 是选 8)。
  • Hashing (下图): 使用哈希函数随机分配。作为 Baseline 存在。
• 【深度解析】
  • 趋势： 现在的趋势是 $k$ 值在变大（从 1 到 2 再到 8），这通常配合着专家总数的增加。

Page 18: 被遗忘的路由方法

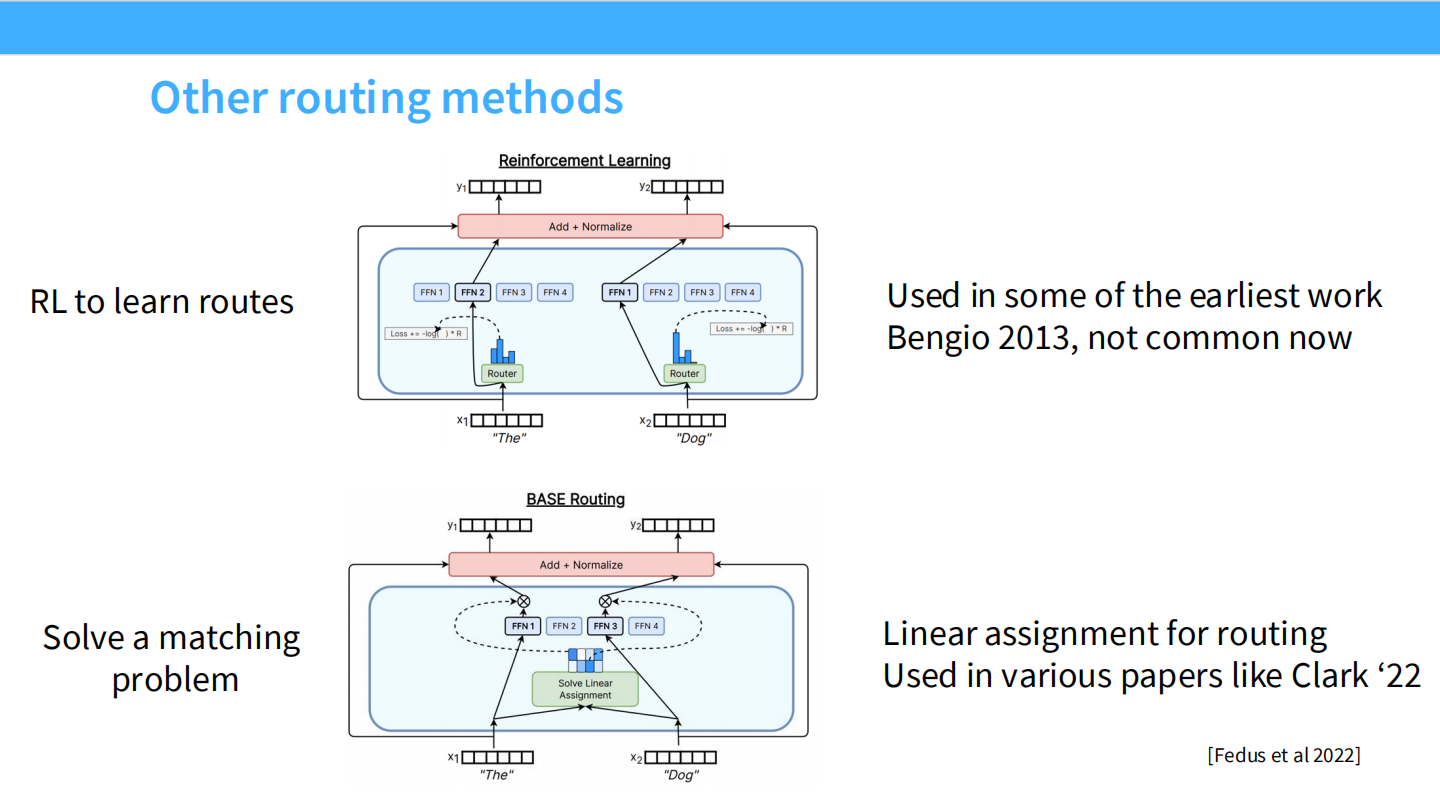
• 【视觉内容】
  • RL (Reinforcement Learning): 引用 Bengio 2013。使用强化学习来训练 Router。
  • Linear Assignment: 引用 Clark ‘22。把路由当成一个二部图匹配问题来解。
• 【深度解析】
  • 为什么不用 RL？ RL 引入了巨大的梯度方差，训练极不稳定，且实现复杂。现在的 Backprop through Softmax 效果已经足够好。

Page 19: Top-K 路由的数学心脏

• 【视觉内容】 核心公式页。
  • 输出公式： $\mathbf{h}t^l = \sum{i=1}^N (g_{i,t} \text{FFN}_i(\mathbf{u}_t^l)) + \mathbf{u}_t^l$。即：MoE 输出 = 加权求和的专家输出 + 残差连接。
  • 门控公式： $g_{i,t}$。通常是 $s_{i,t} = \text{Softmax}(\mathbf{u}_t^T \mathbf{e}_i)$。
  • DeepSeek 的特殊性： 右侧文字注明，Mixtral, DBRX, DeepSeek v3 是在 TopK 选择之后 再做 Softmax（只对选中的那几个专家归一化，而不是对所有专家）。DeepSeek 还在 Softmax 前加了 Sigmoid。
• 【深度解析】
  • Router 本质上就是一个简单的**逻辑回归 (Logistic Regression)**。它学习输入向量与专家向量 $\mathbf{e}_i$ 的相似度。

Page 20: 架构演进 - DeepSeekMoE 的核心创新

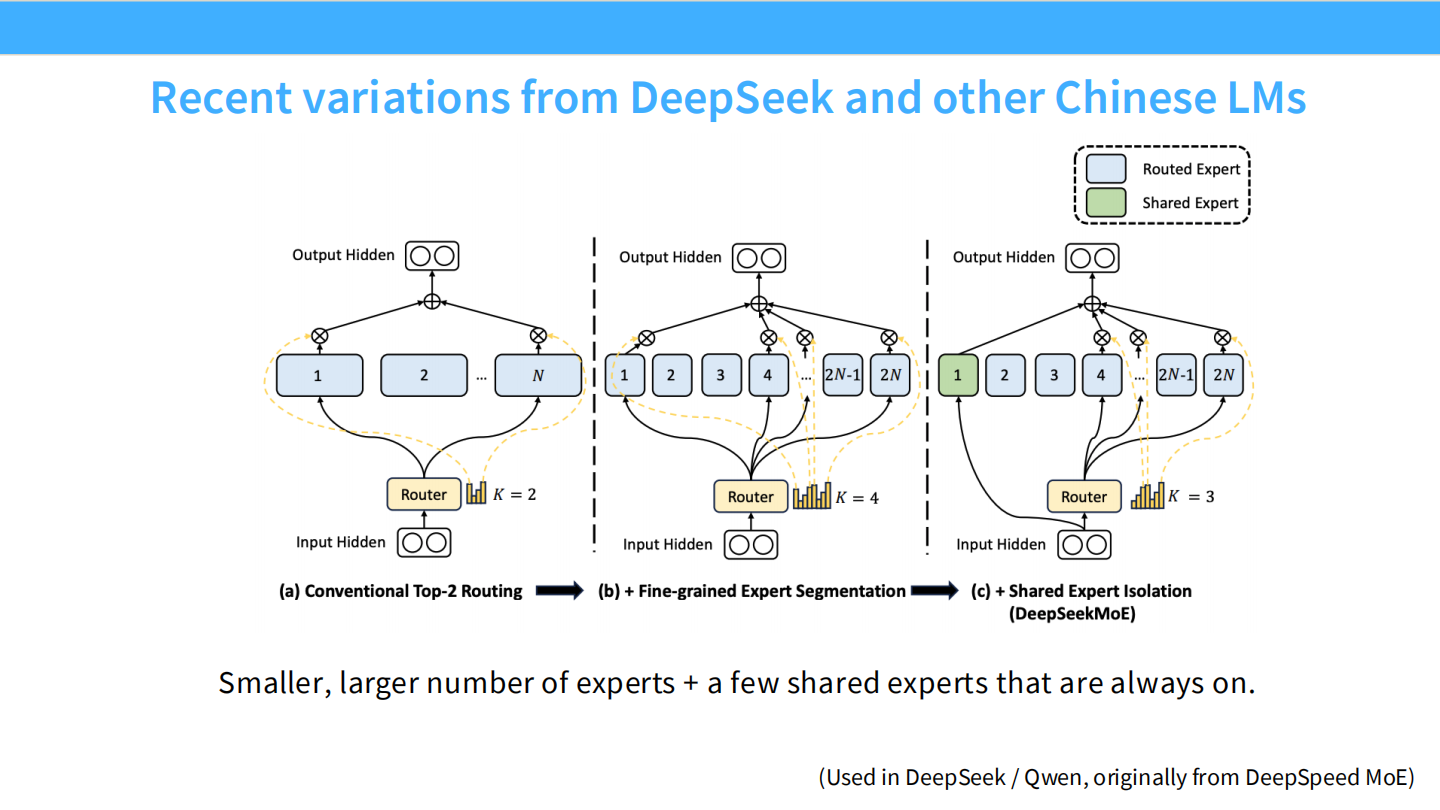
• 【视觉内容】 三种架构演进图。
  • (a) Conventional Top-2: 传统模式（如 Mixtral）。比如 8 个大专家选 2 个。
  • (b) Fine-grained Segmentation: 细粒度切分。把 1 个大专家切成 4 个小专家，增加专家总数。
  • (c) DeepSeekMoE (Shared + Fine-grained): 这是 DeepSeek 的必杀技。
    • Shared Expert (绿色): 总是被选中，不经过 Router。用于捕获通用知识。
    • Routed Expert (蓝色): 细粒度的小专家，由 Router 动态选择。用于捕获长尾/专业知识。
• 【深度解析】
  • 设计哲学： “General knowledge should be shared; specific knowledge should be routed.”（通用知识共享，特定知识路由）。这种设计显著提升了参数利用率。

Page 21: DeepSeek 的消融证据

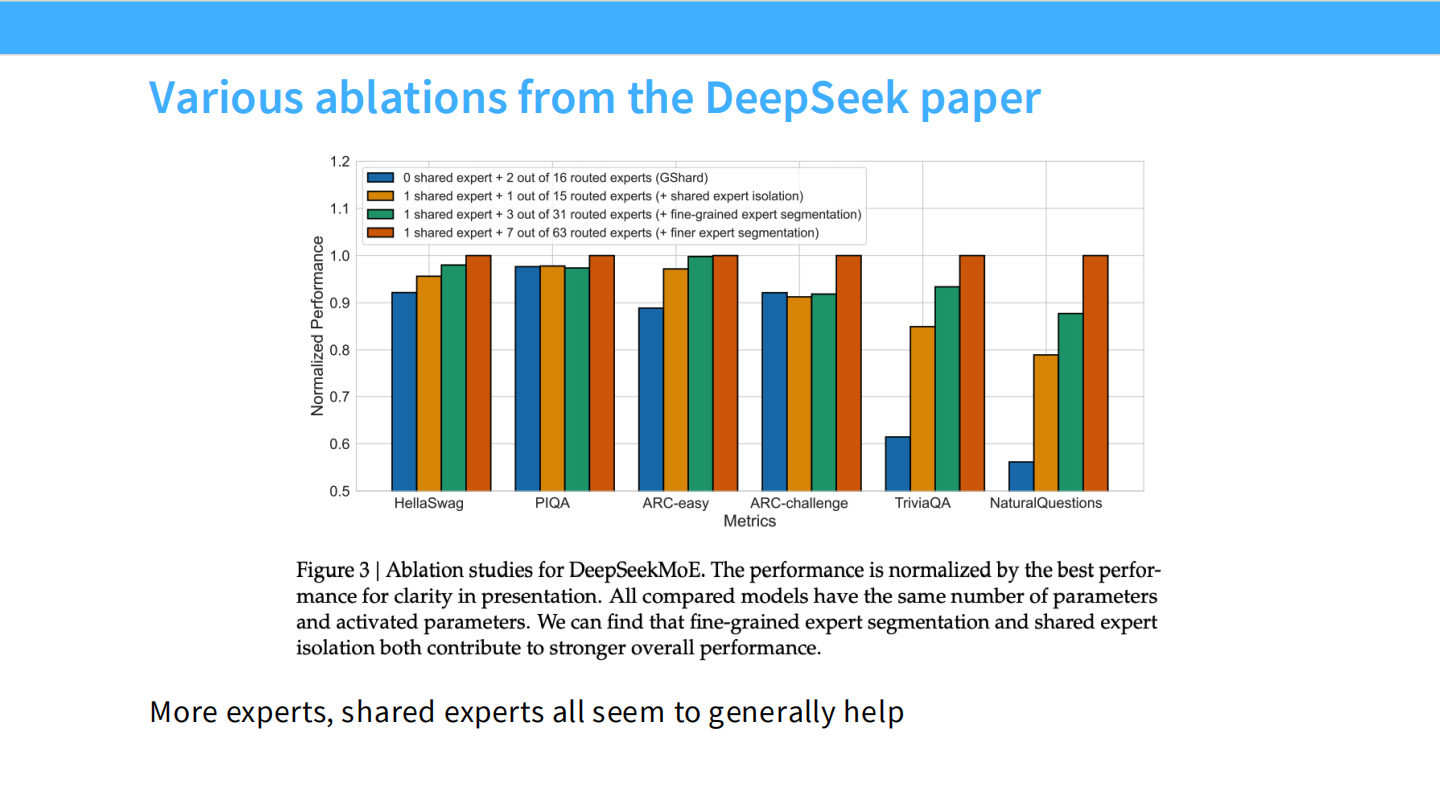
• 【视觉内容】 柱状图对比。
  • 图例： 蓝色（GShard, 无共享）、橙色（大专家+共享）、绿色（细粒度+共享）。
  • 结果： 绿色柱子在 HellaSwag, PIQA, ARC 等所有任务上都是最高的。
• 【深度解析】
  • 结论： 细粒度切分 (Fine-grained) 和 共享专家 (Shared isolation) 两者都对性能有贡献。缺一不可。

Page 22: OlMoE 的不同声音

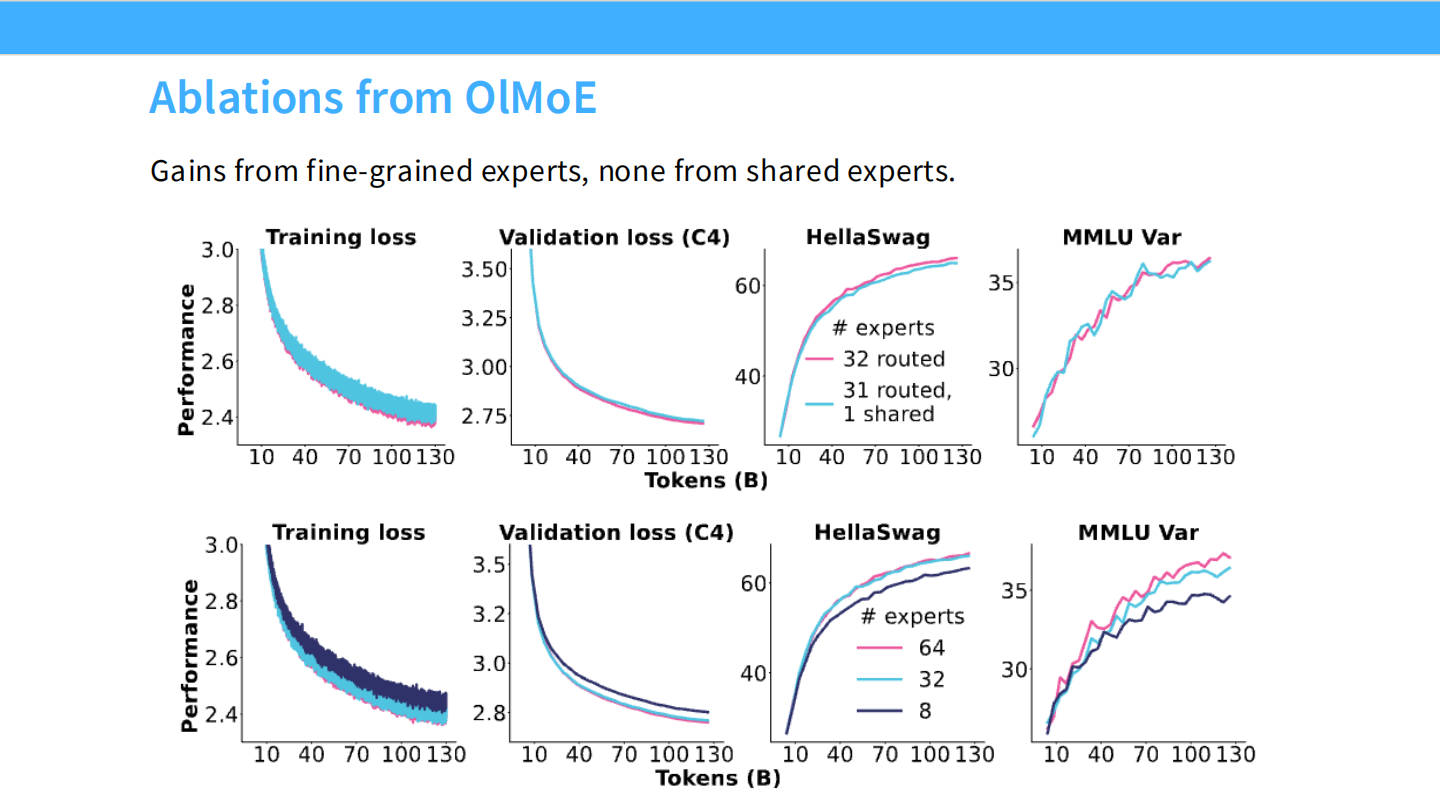
• 【视觉内容】 OlMoE 论文的消融实验。
  • 上图： 32 routed (粉色) 和 31 routed + 1 shared (蓝色) 的曲线完全重合。说明在他们的设置下，共享专家没用。
  • 下图： 64 experts (粉色) 明显优于 32 experts (蓝色)。说明细粒度切分有用。
• 【深度解析】
  • 这表明 “Shared Expert” 是否有效可能取决于具体的模型规模或训练设置，但在 DeepSeek 的大规模模型中已被证实极其有效。

Page 23: 众神参数表 (The Big Table)

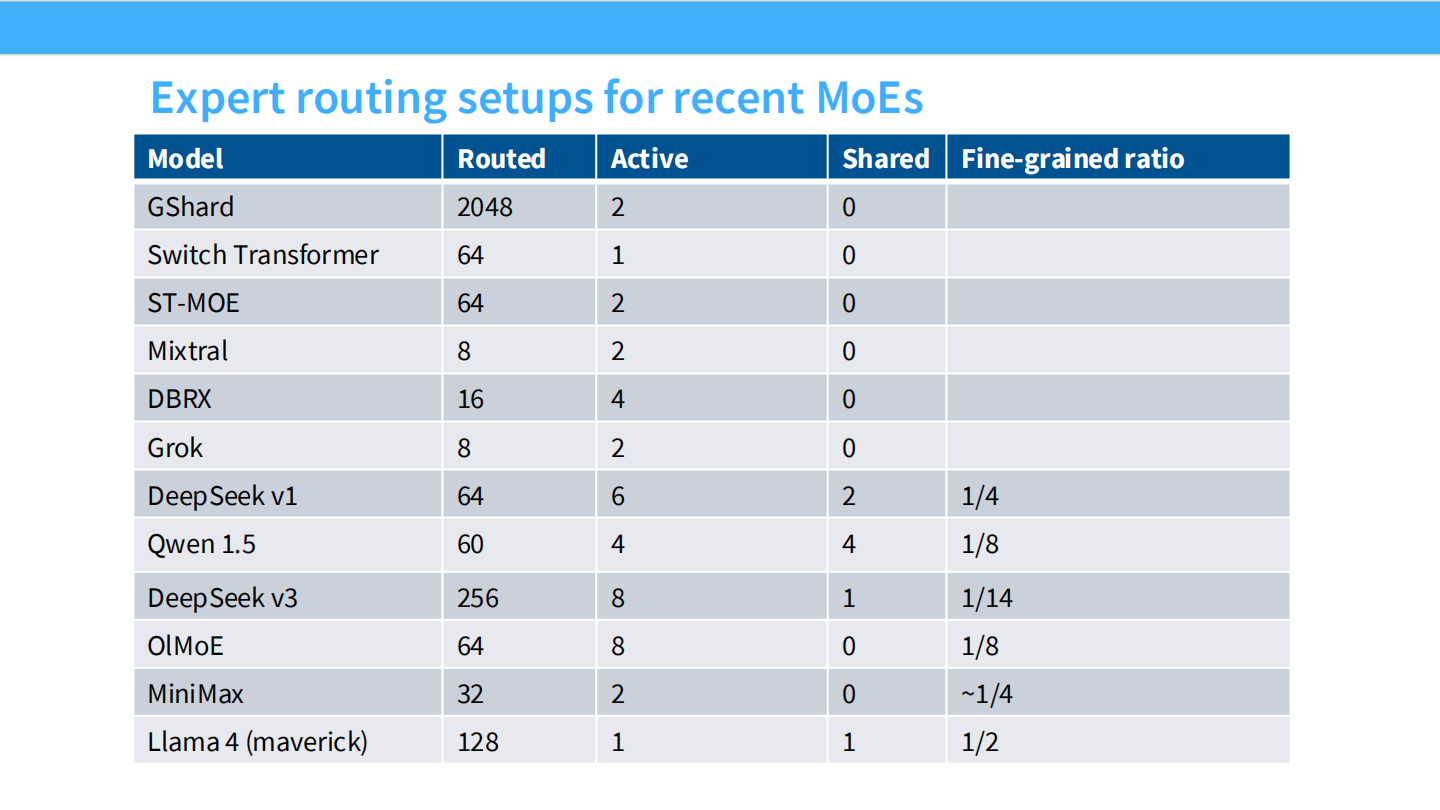
• 【视觉内容】 汇总了所有主流 MoE 的路由设置。
  • Switch Transformer: 64 选 1。
  • Mixtral: 8 选 2。
  • Grok: 8 选 2。
  • DeepSeek v3: 256 选 8 (Routed), 1 个 Shared, 细粒度比率 1/14。
  • Llama 4: 128 选 1, 1 个 Shared。
• 【深度解析】
  • 趋势一目了然： 专家总数在变多（8 -> 64 -> 256），激活专家数也在变多（2 -> 8），且 “Shared Expert” 正在被更多模型（如 Llama 4, Qwen, DeepSeek）采用。

---

Part 3: 训练秘籍与稳定性 (Training & Stability)

Page 24: 训练 MoE 的核心矛盾

• 【视觉内容】 文字描述。
  • 挑战： 稀疏选择 (Top-k) 是离散的操作，**不可导 (not differentiable)**。无法直接用反向传播更新 Router。
  • 解决方案：
    1. RL (太难训)。
    2. Stochastic perturbations (加噪声)。
    3. Heuristic ‘balancing’ losses (启发式平衡损失) —— 这是目前的标准答案。

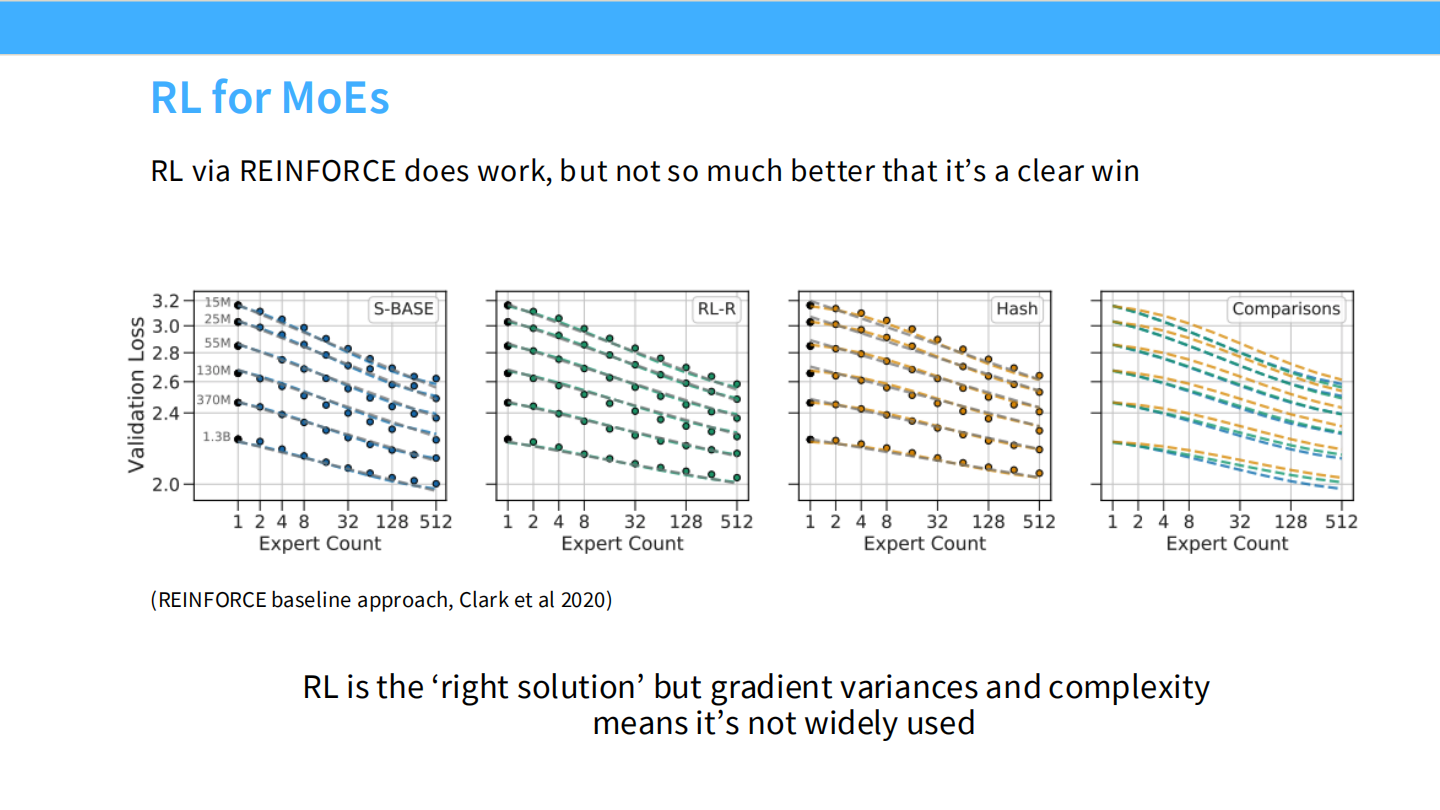
Page 25: 为什么不用 RL？

• 【视觉内容】 散点图对比 S-BASE 和 RL-R。可以看到 RL-R 的点虽然略低（Loss 略好），但并没有质的飞跃。
• 【深度解析】
  • RL via REINFORCE: 虽然理论上可以解决离散求导问题，但它带来了巨大的梯度方差。为了这一点点性能提升而引入 RL 的复杂性，性价比太低 (“not so much better that it’s a clear win”)。

Page 26: 随机近似法 (Stochastic Approximations)

• 【视觉内容】 公式：$H(x)_i = (x \cdot W_g)_i + StandardNormal() \cdot Softplus(…)$。
• 【深度解析】
  • 引用自 Shazeer et al 2017。思路是给 Logits 加上高斯噪声。
  • 作用： 1. 让模型去探索不同的专家（Exploration）；2. 使得 Top-k 操作在某种程度上“平滑化”。

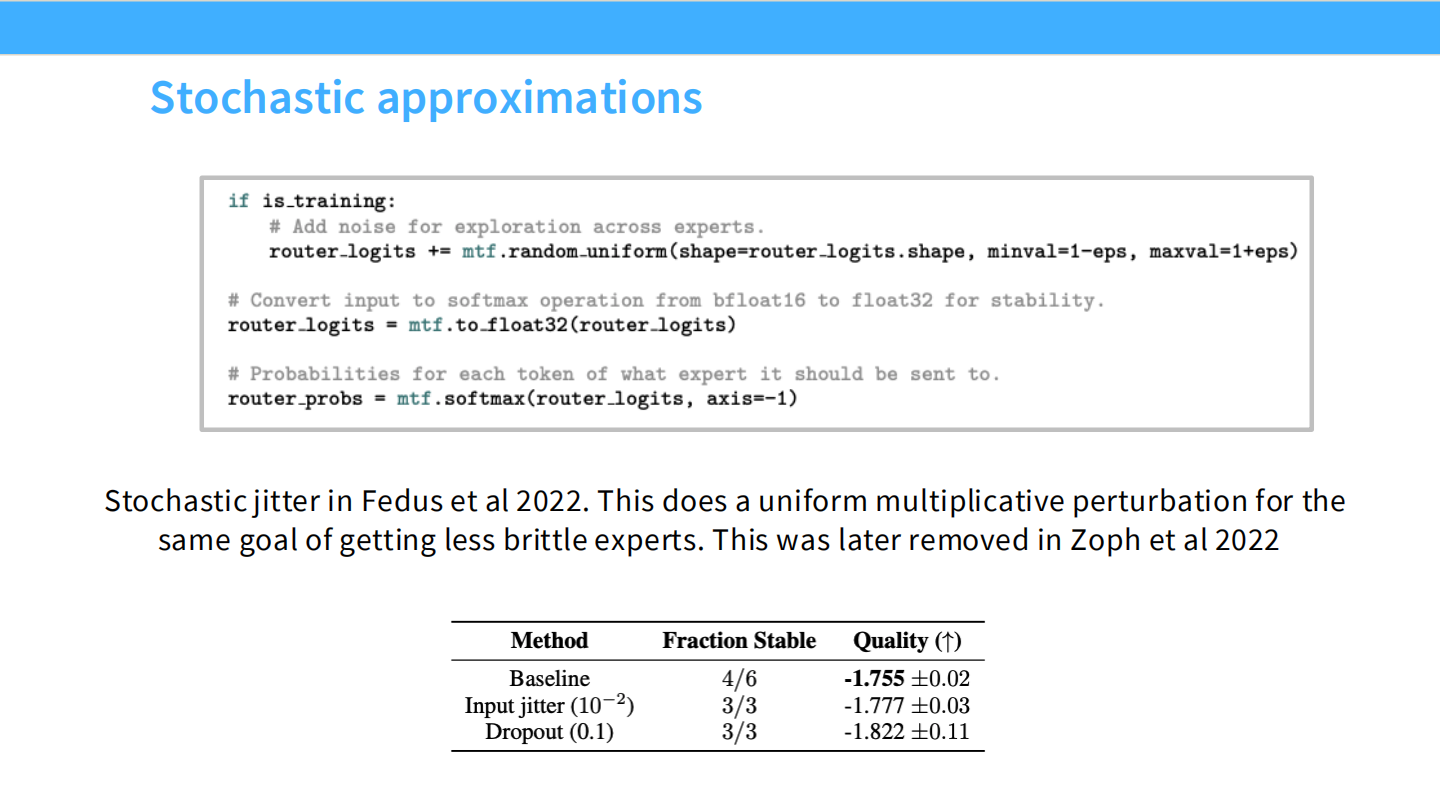
Page 27: Jitter (抖动) 的兴衰

• 【视觉内容】 代码截图 router_logits += mtf.random_uniform(...)。
• 【深度解析】
  • Switch Transformer (Fedus et al 2022) 引入了 Input Jitter（乘性噪声）来增加稳定性。
  • 但后来的研究 (Zoph et al 2022) 发现，表格数据显示 Jitter 并不能提升质量（-1.777 vs -1.755 baseline），甚至可能有害。所以现代 MoE 通常移除了这一步。

Page 28: 辅助负载均衡损失 (Aux Loss)

• 【视觉内容】 Switch Transformer 的经典 Loss 公式：$loss = \alpha \cdot N \cdot \sum f_i \cdot P_i$。
  • $f_i$: 实际上分给专家 $i$ 的 Token 比例（Fraction）。
  • $P_i$: Router 预测给专家 $i$ 的概率总和。
• 【深度解析】
  • 逻辑： 我们希望 $f_i$ 和 $P_i$ 都是均匀的。如果某个专家既被实际大量选中（$f_i$ 高），Router 又极其倾向于它（$P_i$ 高），那么 $f_i \cdot P_i$ 就会很大，导致 Loss 变大。这迫使 Router 把流量分给其他专家。

Page 29: DeepSeek V1/V2 的平衡策略

• 【视觉内容】 两个 Loss 公式。
  • Per-expert balancing: 传统的专家级平衡。
  • Per-device balancing: 这是新东西。公式聚合了同一 Device 上的所有专家。
• 【深度解析】
  • 跨设备通信： 在大规模训练中，如果专家负载均衡了，但这些专家全挤在同一张显卡上，那这张显卡就会因计算过载而拖慢整个集群。所以 DeepSeek 引入了设备级平衡，确保 GPU 之间的负载也是均匀的。

Page 30: DeepSeek V3 的革命 - 无辅助 Loss (Aux-loss-free)

• 【视觉内容】 关键公式：$g’{i,t} = \begin{cases} s{i,t}, & s_{i,t} + b_i \in \text{Topk}(…) \ 0, & \text{otherwise} \end{cases}$。
• 【深度解析】
  • 痛点： 传统的 Aux Loss 会干扰模型的主任务（Cross-Entropy），因为模型为了满足负载均衡，不得不去选一些“次优”的专家，导致性能下降。
  • DeepSeek 解法： 彻底去掉 Aux Loss。改用一个动态更新的偏置项 **Bias ($b_i$)**。
  • 机制： 如果专家 $i$ 负载太重，就降低 $b_i$，让它在 Top-k 排序中得分变低，自然就选不中了。这种反馈是解耦的，不影响梯度更新。

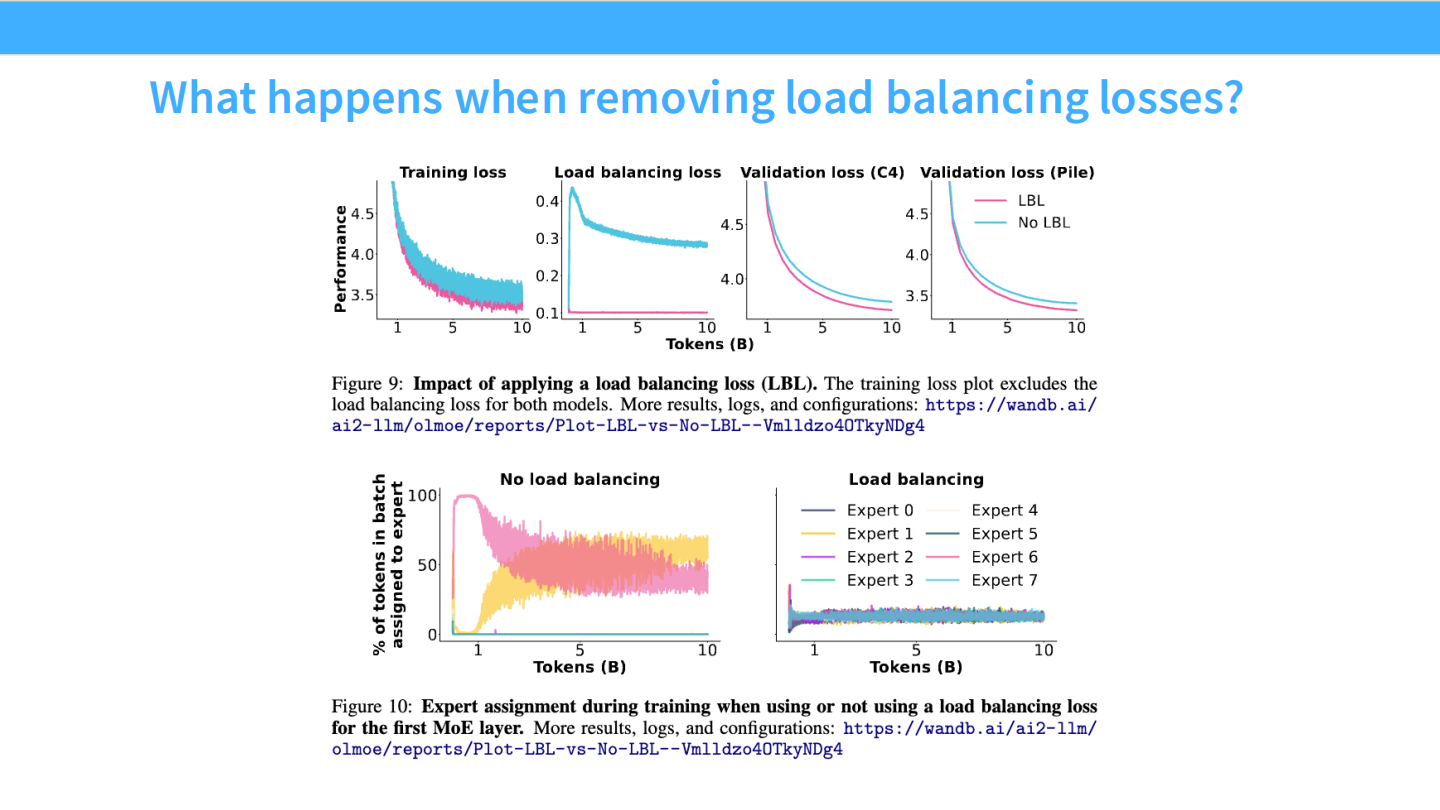
Page 31: 路由崩塌 (Routing Collapse)

• 【视觉内容】
  • 上图： Loss 曲线。No LBL (无负载均衡，蓝色) 的 Loss 居高不下。
  • 下图： 专家分配热力图。左侧 “No load balancing” 显示，Expert 0 和 Expert 6 占据了 100% 的宽度，其他专家全是 0。
• 【深度解析】
  • 这解释了为什么要搞负载均衡。如果不加干预，MoE 会迅速退化：Router 发现某两个专家稍微好一点点，就疯狂把所有 Token 往那里塞，其他专家得不到训练，差距越来越大，最终导致模型崩塌。

---

Part 4: 系统工程与 Upcycling (Systems & Initialization)

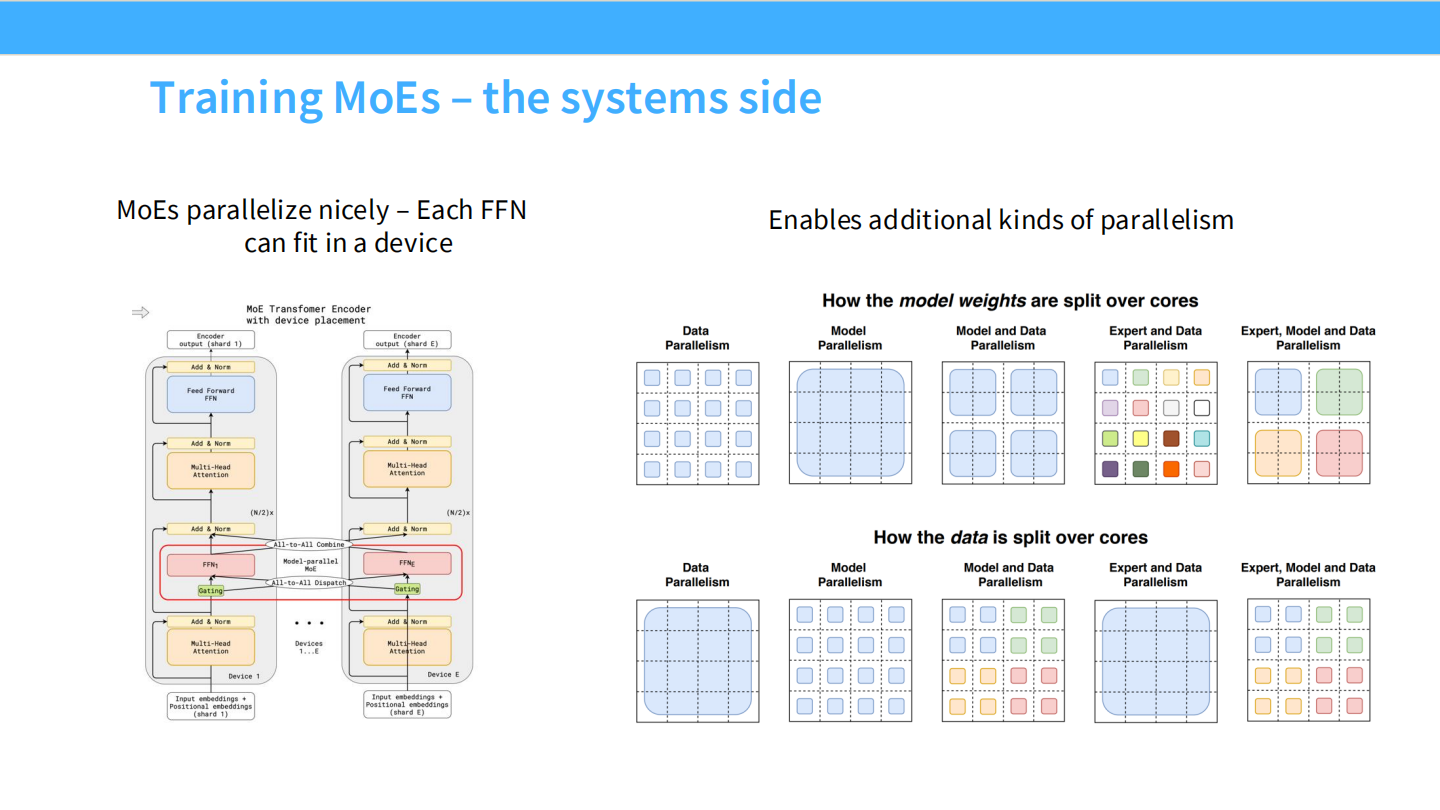
Page 32: 专家并行 (Expert Parallelism)

• 【视觉内容】 网格图展示了数据 (Data) 和模型权重 (Model) 在不同 Core 上的切分方式。
  • 对比了 Model Parallelism, Data Parallelism, Expert Parallelism。
• 【深度解析】
  • Expert Parallelism (EP): 这是 MoE 独有的。我们将不同的专家（FFN）物理放置在不同的 GPU 上。当 Router 分发 Token 时，实际上是在进行跨 GPU 的网络通信（All-to-All）。这要求极高的网络带宽。

Page 33: MegaBlocks 与块稀疏计算

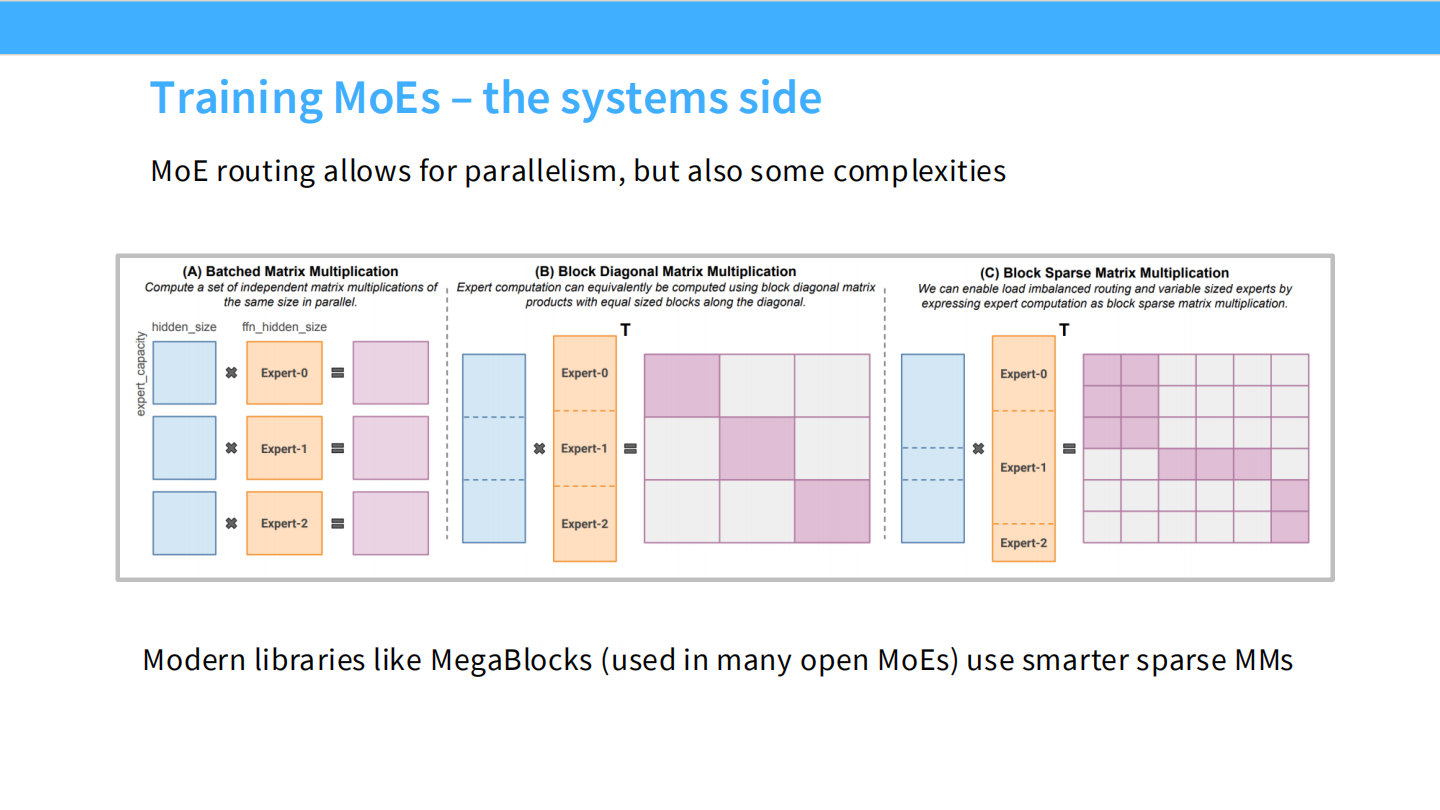
• 【视觉内容】 矩阵乘法示意图。
  • (A) Batched MM: 需要 Padding，浪费计算。
  • (C) Block Sparse Matrix Multiplication: 矩阵块是参差不齐的，直接计算。
• 【深度解析】
  • 问题： 不同专家分到的 Token 数量是不一样的（变长）。传统做法是 Pad 到最大长度，这很浪费。
  • 解法： 使用 MegaBlocks 这样的现代库，支持块稀疏矩阵乘法，可以高效处理负载不均的变长序列，大幅提升训练效率。

Page 34: Token Dropping 与随机性

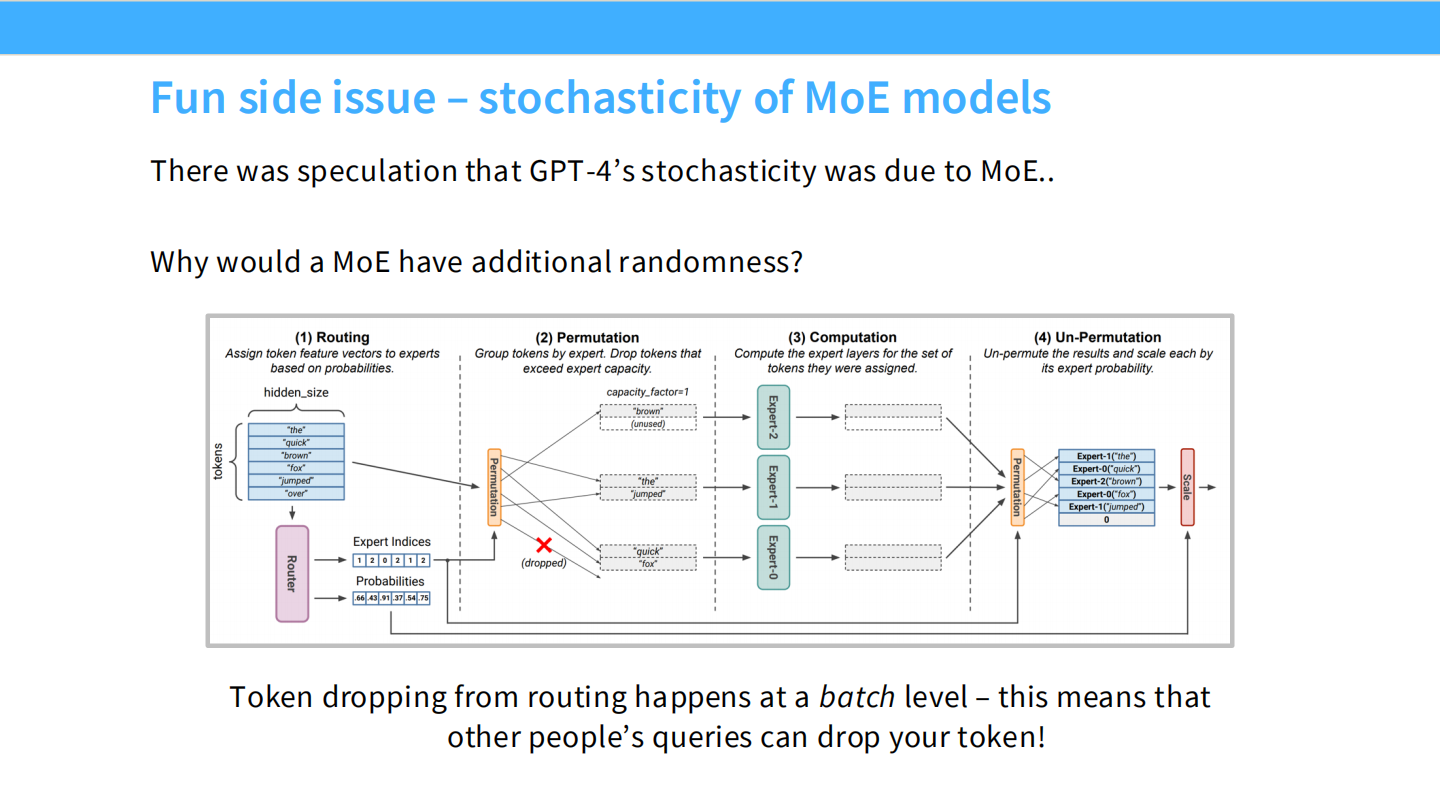
• 【视觉内容】 流程图。中间的 capacity_factor=1 显示，如果 Token 过多（超过容量），多余的 Token 会被 **dropped (画叉)**。
• 【深度解析】
  • GPT-4 的随机性之谜： 早期 GPT-4 即使 Temperature=0 输出也不稳定。原因就在于此。
  • MoE 为了并行效率，每个专家每轮能处理的 Token 数有上限。如果同一个 Batch 里其他人的请求挤占了热门专家，你的 Token 就可能被丢弃（或被迫走其他路），导致输出变化。

Page 35: 稳定性 - Router 精度

• 【视觉内容】 文字框解释 $exp(128.5)$ 在 bfloat16 下会溢出为无穷大。
• 【深度解析】
  • 大坑： 训练大模型通常用 BF16 加速。但在计算 Router 的 Softmax 时，如果 Logits 稍微大一点（比如 100），$e^{100}$ 就会超出 BF16 的表示范围，导致数值错误。
  • 解法： **”Use Float 32 just for the expert router”**。这一小部分计算必须用全精度。

Page 36: 稳定性 - Z-loss

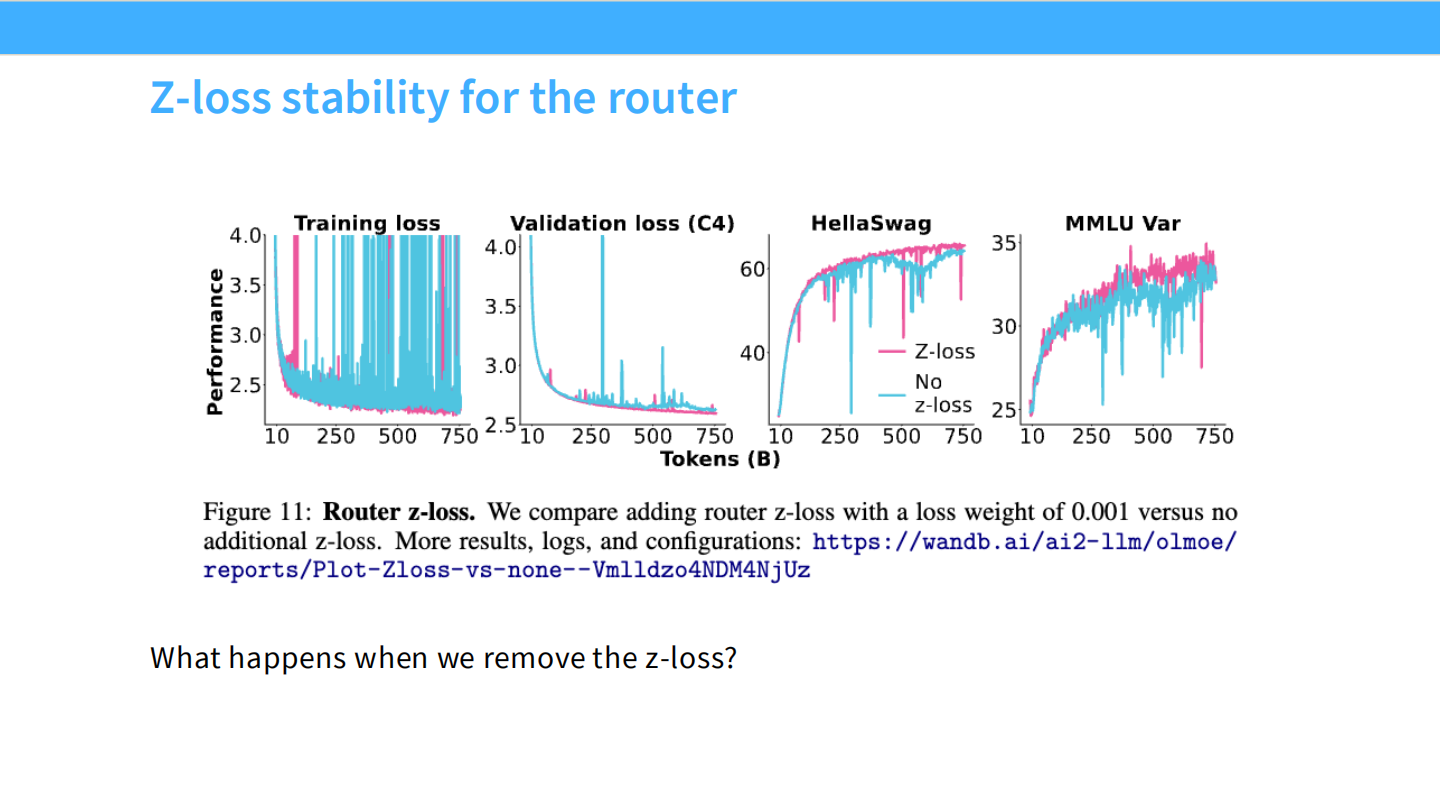
• 【视觉内容】 Loss 曲线。
  • 蓝色 (No z-loss): 曲线充满了剧烈的震荡和尖峰 (Spikes)。
  • 粉色 (Z-loss): 曲线非常平滑。
• 【深度解析】
  • Z-loss 公式： $L_z(x) = \frac{1}{B} \sum \log^2 \sum e^x$。
  • 作用： 它惩罚过大的 Logits 值，迫使 Router 的输出保持在 0 附近。这从根本上减少了 Softmax 溢出的风险，是 MoE 稳定训练的必备技巧。

Page 37: 微调难题与 SFT

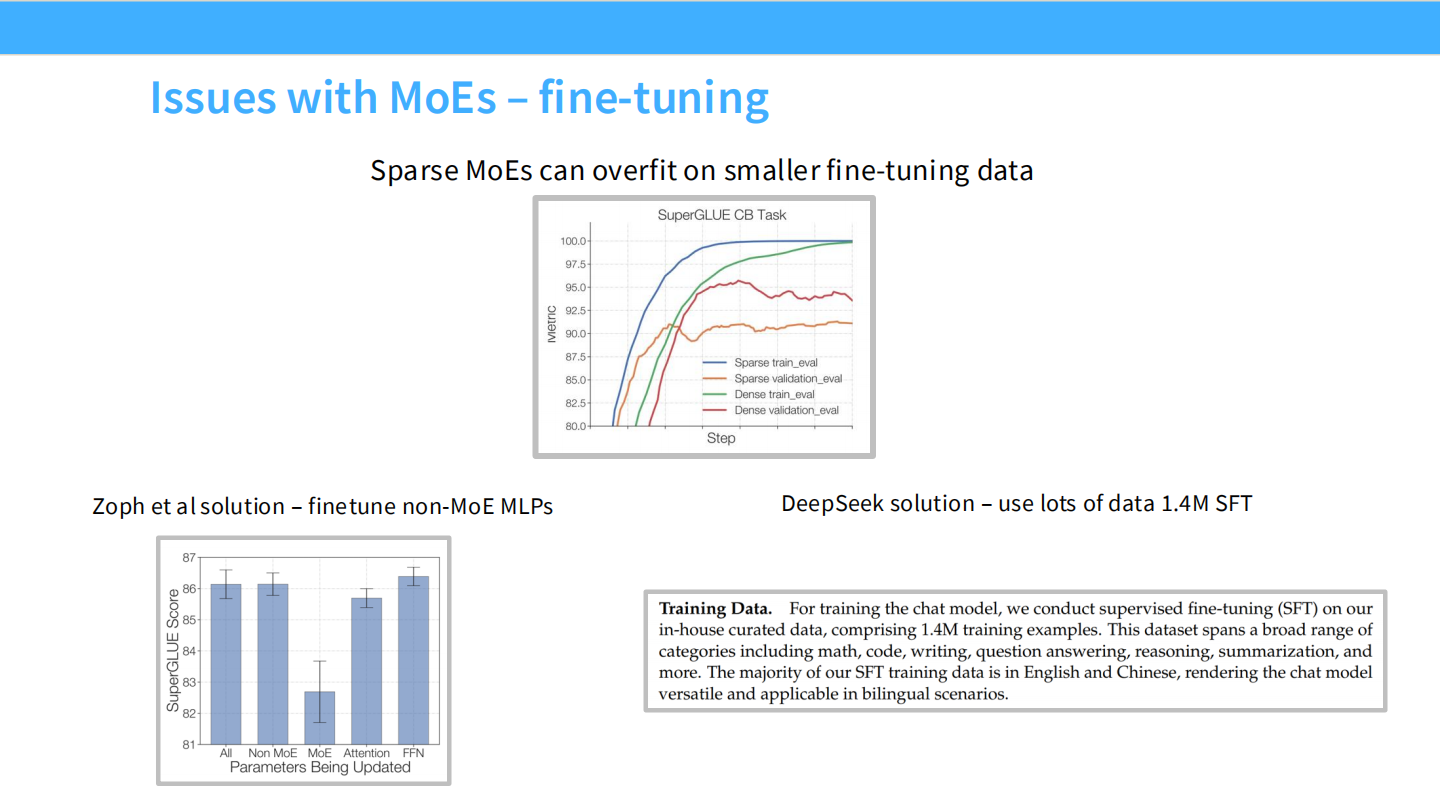
• 【视觉内容】
  • 上图： 微调时的 Validation Loss。Sparse 模型（橙线）比 Dense 模型（红线）上升得更快，说明过拟合更严重。
  • 文字： “DeepSeek solution – use lots of data 1.4M SFT”。
• 【深度解析】
  • MoE 参数量巨大，在小数据集上微调极易过拟合。
  • DeepSeek 的暴力美学：用海量数据 (1.4M 条) 进行 SFT，直接把模型喂饱，解决了过拟合问题。

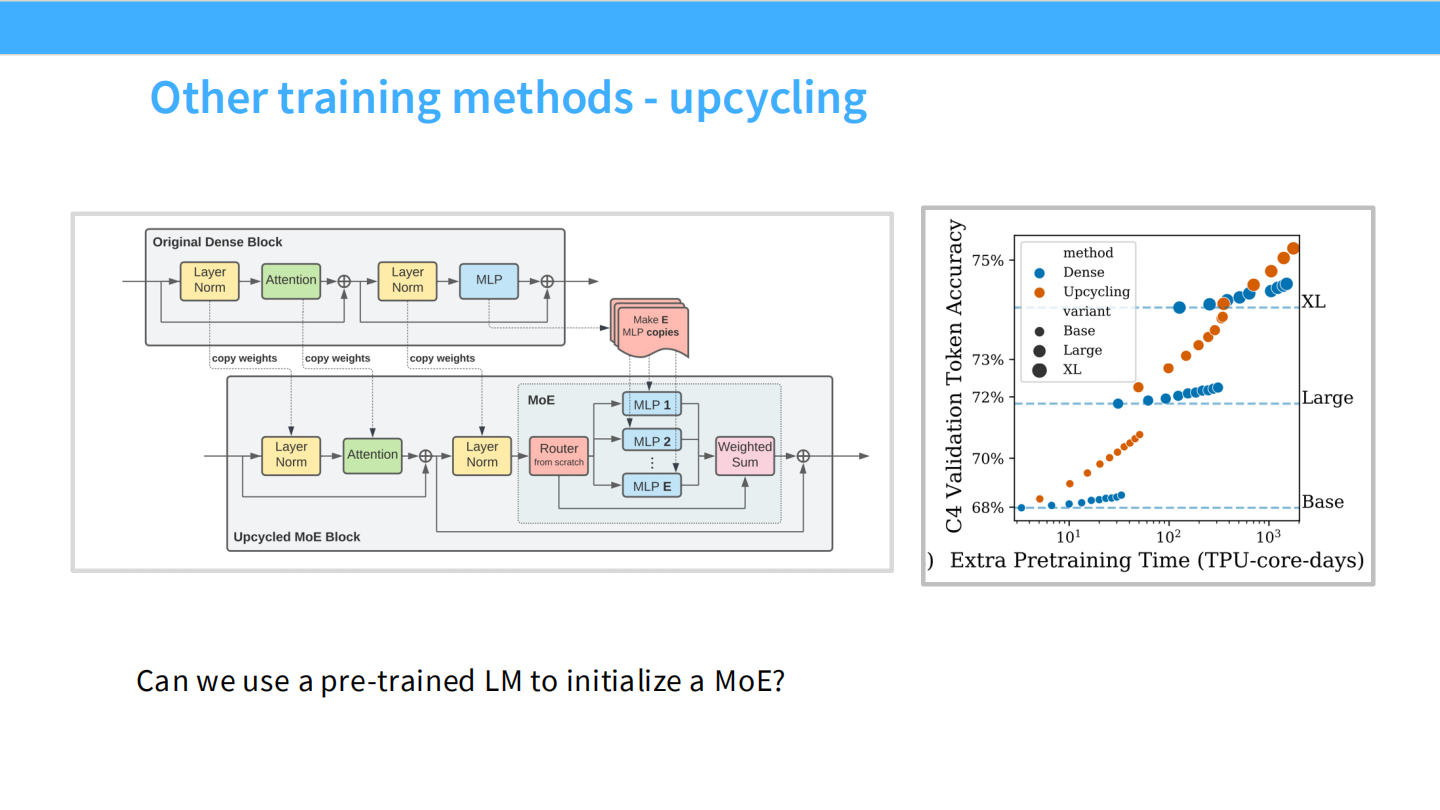
Page 38: Upcycling (升级/热启动)

• 【视觉内容】 流程图。展示了如何把一个 “Original Dense Block” (MLP) 复制多份，变成 “Upcycled MoE Block” (MLP 1…E)。
• 【深度解析】
  • 省钱妙招： 你不需要从头训练一个 MoE。你可以拿一个训练好的 Dense 模型，把它的 FFN 复制 8 份作为 8 个专家，初始化一个 MoE，然后继续训练 (Continue Pretraining)。这能节省大量的预训练时间。

Page 39: Upcycling 案例 - MiniCPM

• 【视觉内容】 表格。MiniCPM-MoE (58.11) 优于 MiniCPM-2.4B (51.13)。
• 【深度解析】
  • MiniCPM 证明了 Upcycling 的有效性：仅需 ~520B tokens 的额外训练，就能让模型性能上一个台阶。

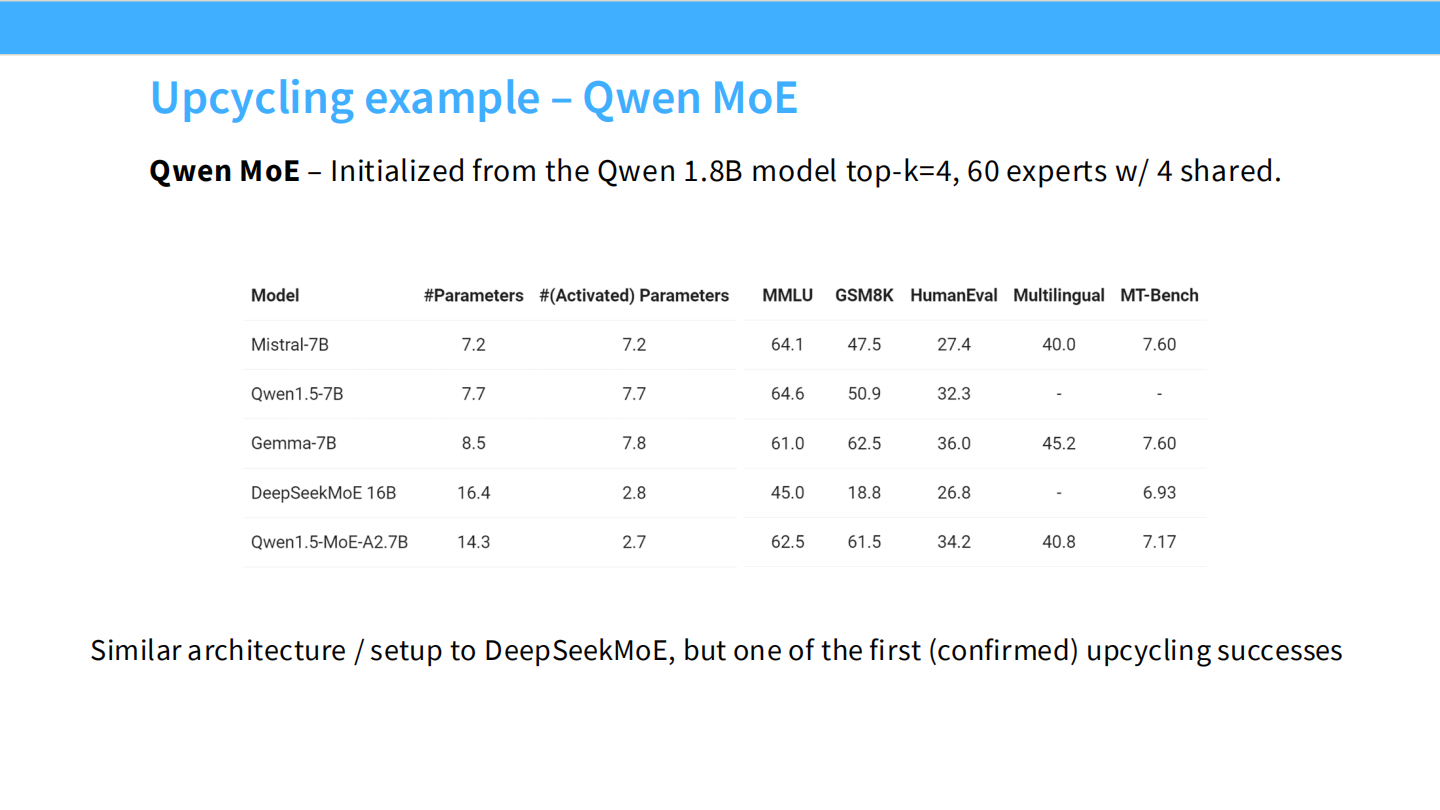
Page 40: Upcycling 案例 - Qwen MoE

• 【视觉内容】 表格。Qwen1.5-MoE-A2.7B 的表现优于同级 Dense。
• 【深度解析】
  • Qwen MoE 同样是基于 Qwen 1.8B Dense 模型 Upcycling 而来的。这是业界公认的高效路径。

---

Part 5: DeepSeek 架构深度解构 (DeepSeek V1-V3 Breakdown)

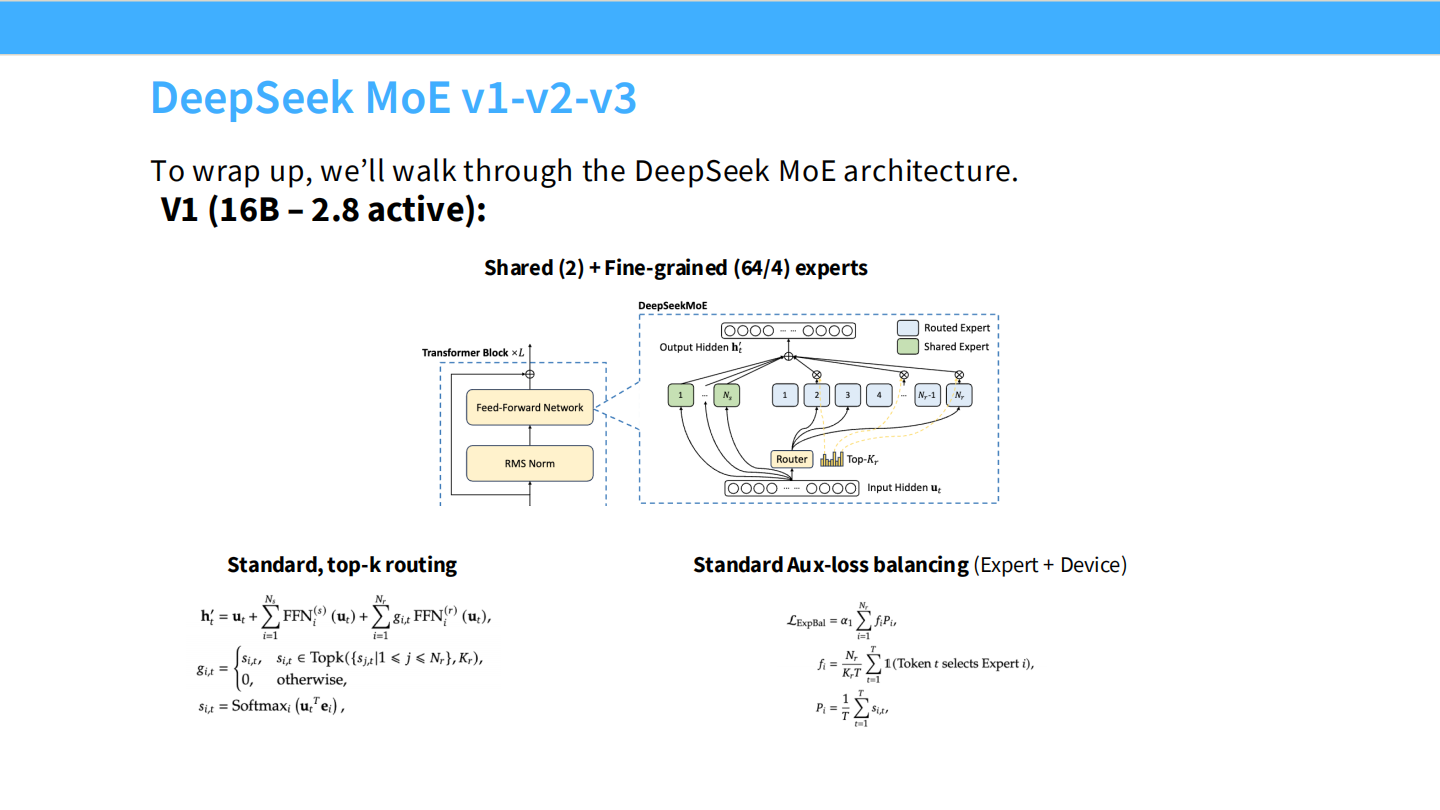
Page 41: DeepSeek MoE V1

• 【视觉内容】 V1 架构图。
• 【深度解析】
  • 规格： 16B 总参数，2.8B 激活。
  • 架构： 确立了 Shared (2个) + Fine-grained (64个) 的基本形态。
  • 限制： 此时还在用标准的 Top-k 路由和 Aux Loss。

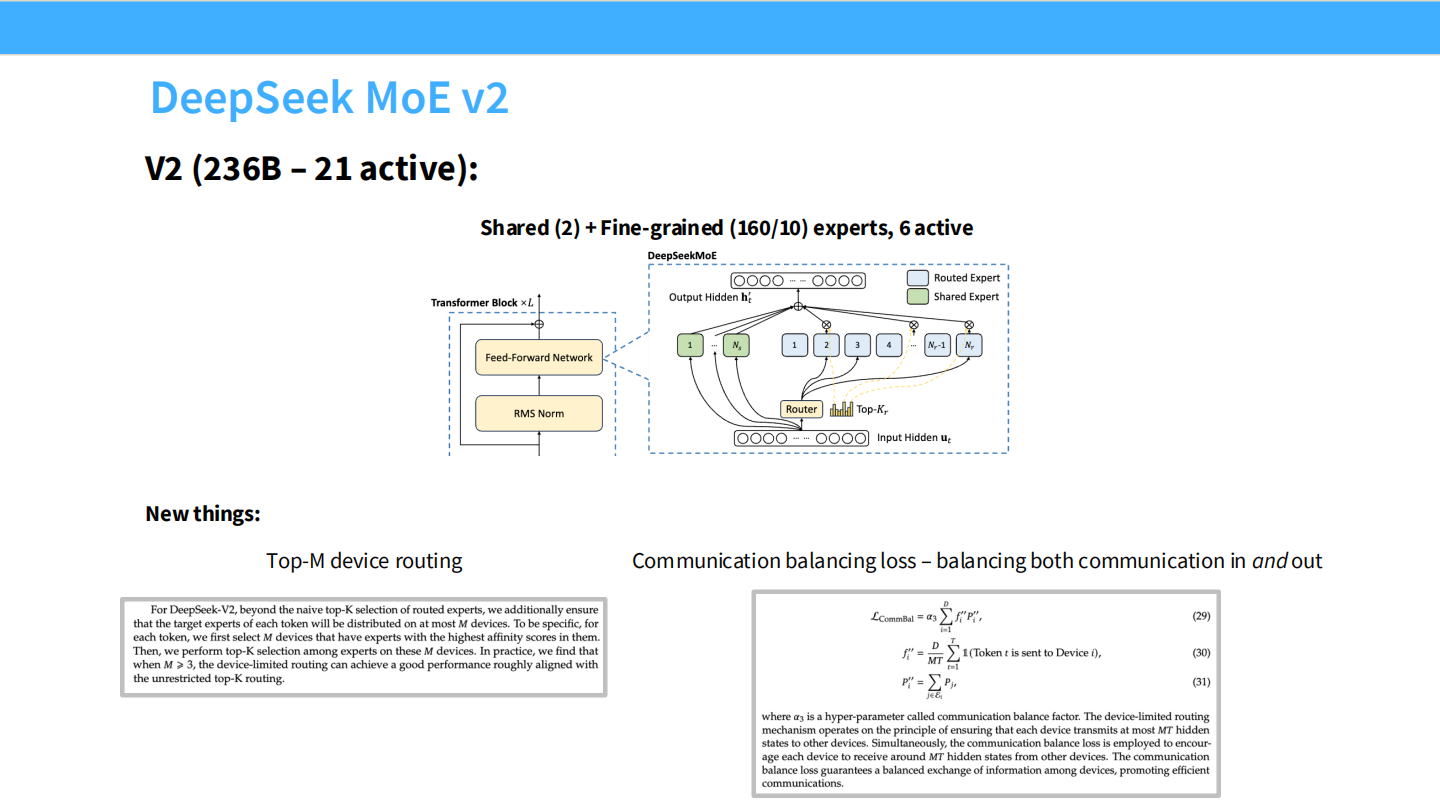
Page 42: DeepSeek MoE V2

• 【视觉内容】 V2 架构图。
• 【深度解析】
  • 规格： 扩大到 236B 总参数，21B 激活。
  • 创新： 引入 Top-M Device Routing。为了解决数千张显卡并行的通信瓶颈，V2 限制了每个 Token 最多只能去 M 个 Device，防止通信风暴。

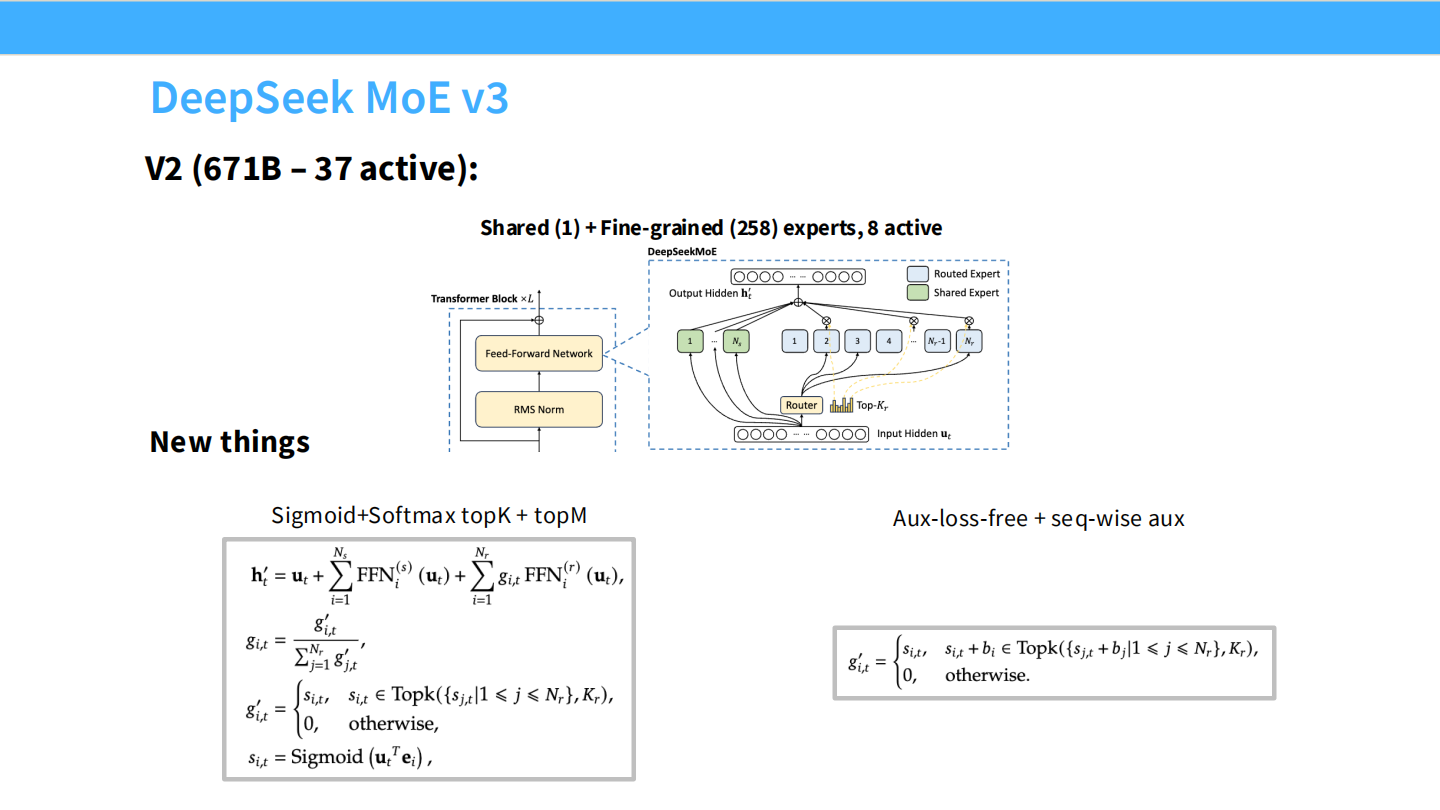
Page 43: DeepSeek MoE V3 (完全体)

• 【视觉内容】 V3 架构图。
• 【深度解析】
  • 规格： 671B 总参数，37B 激活。这是目前的旗舰配置。
  • 专家： 1 个 Shared Expert，256 个 Fine-grained Experts（选 8 个）。
  • 核心升级：
    1. Sigmoid Routing: 也就是图中的 Sigmoid(u^T e)，能更好地区分专家。
    2. Aux-loss-free: 彻底移除了 Aux Loss，用 Bias 动态平衡，性能不再受损。

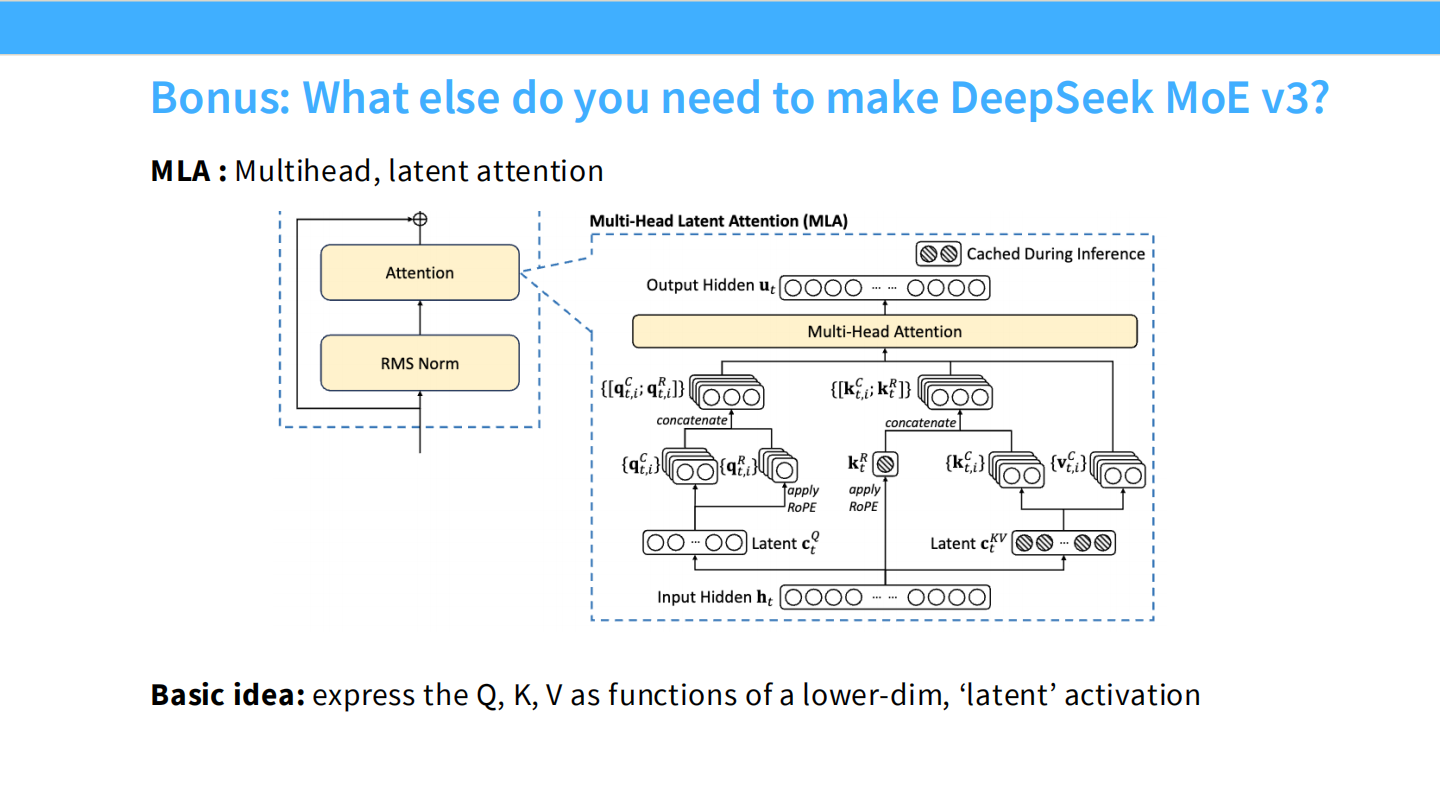
Page 44: V3 黑科技 - MLA (Multi-Head Latent Attention)

• 【视觉内容】 MLA 架构示意图。左侧是 Attention 模块，右侧放大了 KV Cache 的处理细节。
• 【深度解析】
  • 背景： MoE 模型虽然计算快，但参数量大，显存占用高，尤其是 KV Cache 在长文本下是巨大的负担。
  • 原理： MLA 将 Key 和 Value 压缩 进一个低维的 Latent 向量 ($c_{KV}$)。在推理时，不需要存储巨大的 KV 矩阵，只需要存储压缩后的向量。这极大地降低了显存需求，提升了推理吞吐量。

Page 45: MLA 与 RoPE 的兼容性

• 【视觉内容】 复杂的公式推导。红色部分标注了 RoPE (旋转位置编码) 对矩阵性质的破坏。
• 【深度解析】
  • 难题： RoPE 对位置敏感，如果直接把 Key 压缩了，位置信息就丢了，RoPE 会失效。
  • DeepSeek 解法： 混合 Key 策略。把 Key 劈成两半：
    1. Latent 部分： 负责内容，被强力压缩。
    2. Pe 部分： 负责位置，保留原始维度，专门用来做 RoPE 旋转。
  • 这样既享受了压缩带来的显存红利，又保留了 RoPE 的长窗口能力。

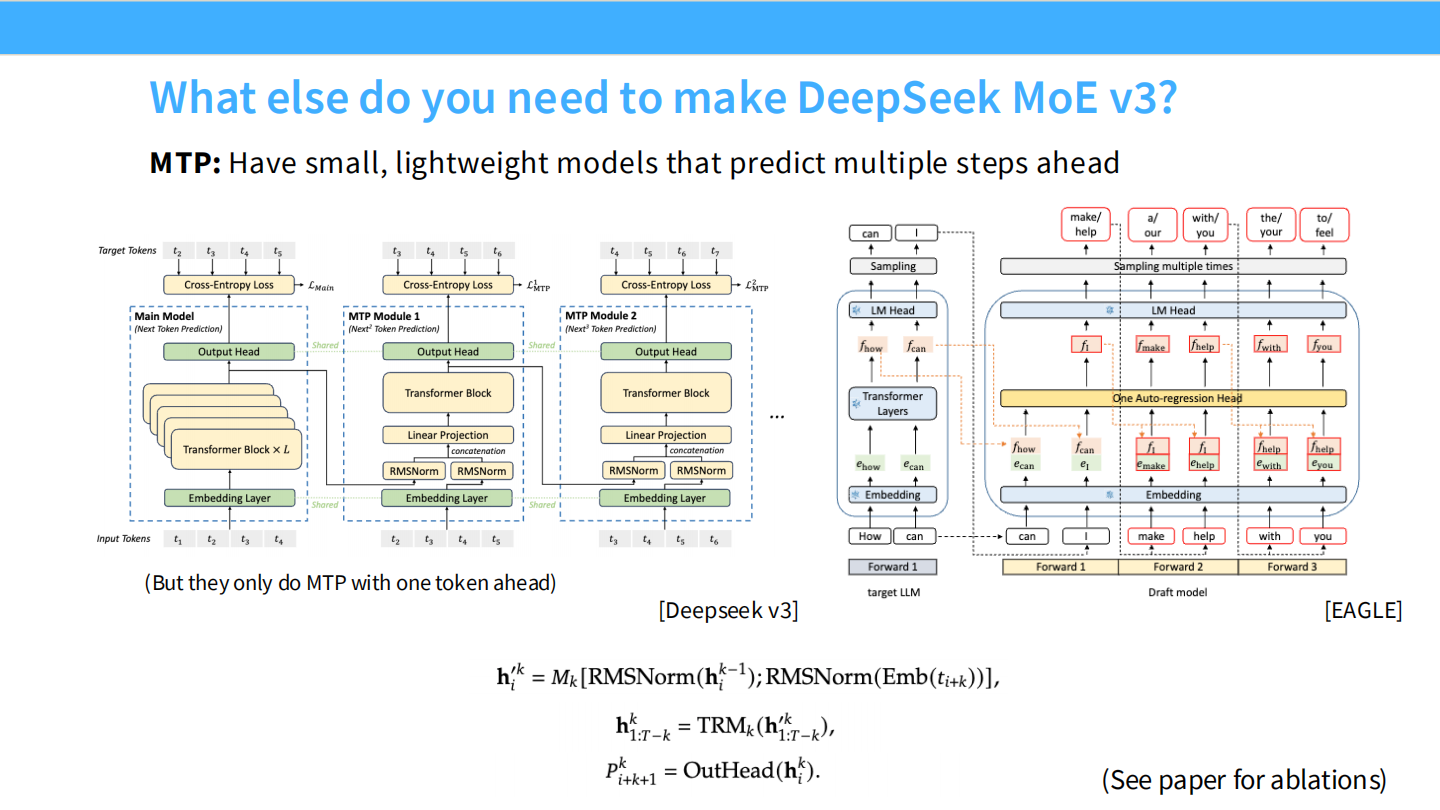
Page 46: V3 黑科技 - MTP (Multi-Token Prediction)

• 【视觉内容】
  • 左图 (DeepSeek V3): Main Model 输出后，并没有结束，而是接了一个 MTP Module 1 和 Module 2。
  • 右图 (EAGLE): 类似的学术界架构。
• 【深度解析】
  • 原理： 训练模型时，不只让它预测下一个词 (Token $t+1$)，还让它顺便预测下下个词 (Token $t+2$)。
  • 收益：
    1. 训练信号更强： 迫使模型学会规划，而不仅仅是短视的预测。
    2. 推理加速： 在推理时，可以利用这个预测头进行**投机采样 (Speculative Decoding)**，如果预测准了，一次就能生成两个词，速度翻倍。

Page 47: 课程总结 (Summary)

• 【视觉内容】 总结页。
• 【深度解析】
  1. 稀疏即正义： MoE 证明了我们不需要每次都激活全脑，稀疏计算是扩展模型规模的必经之路。
  2. Top-k 足矣： 尽管理论很复杂，但简单的 Top-k 启发式路由在工程上最管用。
  3. 未来已来： 大量的实证（DeepSeek, GPT-4）表明，MoE 是高效、低成本且高性能的架构，是当前 LLM 的终极形态。