大模型从0到1｜第十七课：手把手讲解GRPO

课程链接：Stanford CS336 Spring 2025 - Lecture 17

上一讲：基于可验证奖励的强化学习概览 (Policy Gradient)
本讲：深入探讨策略梯度的机制（例如：GRPO）

1. 语言模型的强化学习设置 (RL Setup for Language Models)

状态 (State) s：提示词 (prompt) + 截至目前生成的回复 动作 (Action) a：生成下一个 token

奖励 (Rewards) R：回复有多好；我们将关注： * 结果奖励 (Outcome rewards)：取决于整个回复 * 可验证奖励 (Verifiable rewards)：其计算是确定性的 * 折扣 (Discounting) 和自举 (Bootstrapping) 的概念不太适用 * 示例：“... Therefore, the answer is 3 miles.”

转移概率 (Transition probabilities) T(s' | s, a)：确定性的 s' = s + a * 可以进行规划 / 测试时计算 (test-time compute)（与机器人技术不同） * 状态实际上是构造出来的（与机器人技术不同），因此有很多灵活性

策略 (Policy) π(a | s)：就是一个语言模型（经过微调的）

Rollout/episode/trajectory：s → a → ... → a → a → R

目标 (Objective)：最大化期望奖励 E[R] （其中期望是针对提示词 s 和回复 token a 取的）

2. 策略梯度 (Policy Gradient)

为了符号简单起见，让 a 表示整个回复。

我们希望最大化关于策略 π 的期望奖励： E[R] = ∫ p(s) π(a | s) R(s, a)

显而易见的方法是求梯度： ∇ E[R] = ∫ p(s) ∇ π(a | s) R(s, a) ∇ E[R] = ∫ p(s) π(a | s) ∇ log π(a | s) R(s, a) ∇ E[R] = E[∇ log π(a | s) R(s, a)]

朴素策略梯度 (Naive policy gradient)： * 采样提示词 s，采样回复 a ~ π(a | s) * 基于 ∇ log π(a | s) R(s, a) 更新参数（与 SFT 相同，但由 R(s, a) 加权）

设置： R(s, a) ∈ {0, 1} = 回复是否正确 * 朴素策略梯度仅在正确回复上更新 * 像 SFT，但数据集随策略变化而随时间变化

挑战：高噪声/方差 在这个设置中，稀疏奖励（很少有回复得到奖励 1，大多数得到 0） 对比：在 RLHF 中，奖励模型（从成对偏好中学习）更加连续

基线 (Baselines)

回忆 ∇ E[R] = E[∇ log π(a | s) R(s, a)] ∇ log π(a | s) R(s, a) 是 ∇ E[R] 的无偏估计，但也许还有其他方差更低的估计...

示例：两个状态 * s1: a1 → 奖励 11, a2 → 奖励 9 * s2: a1 → 奖励 0, a2 → 奖励 2 不希望 s1 → a2（奖励 9），因为 a1 更好；希望 s2 → a2（奖励 2），但是 9 > 2。

想法： 最大化基线奖励：E[R - b(s)] 这只是 E[R] 平移了一个不依赖于策略 π 的常数 E[b(s)] 我们基于 ∇ log π(a | s) (R(s, a) - b(s)) 更新

应该使用什么 b(s)？

示例：两个状态 假设在 (s, a) 上均匀分布且 |∇ π(a | s)| = 1 朴素方差 = std([11, 9, 0, 2]) = 5.26 定义基线 b(s1) = 10, b(s2) = 1 基线方差 = std([11-10, 9-10, 0-1, 2-1]) = std([1, -1, -1, 1]) = 1.15 方差显著降低！

最优 b*(s) = E[(∇ π(a | s))^2 R | s] / E[(∇ π(a | s))^2 | s]（对于单参数模型） 这很难计算... ...所以启发式方法是使用平均奖励： b(s) = E[R | s] 这仍然很难计算，必须进行估计。

优势函数 (Advantage functions)

这种 b(s) 的选择与优势函数有关。 * V(s) = E[R | s] = 从状态 s 开始的期望奖励 * Q(s, a) = E[R | s, a] = 从状态 s 采取动作 a 的期望奖励 （注意：这里 Q 和 R 是相同的，因为我们假设 a 包含所有动作且我们要么有结果奖励。）

定义 (优势)： A(s, a) = Q(s, a) - V(s) 直觉：动作 a 比从状态 s 预期的好多少

如果 b(s) = E[R | s]，那么基线奖励与优势完全相同！ E[R - b(s)] = A(s, a)

一般来说： * 理想情况：E[∇ log π(a | s) R(s, a)] * 估计：∇ log π(a | s) δ δ 有多种选择，我们稍后会看到。

CS224R lecture notes

3. 实战演练 (Training walkthrough)

Group Relative Policy Optimization (GRPO) Link * 对 PPO 的简化，移除了 critic（价值函数） * 利用 LM 设置中的组结构（每个提示词多个回复），这提供了一个自然的基线 b(s)。

简单任务 (Simple task)

任务：排序 n 个数字

提示词：n 个数字

prompt = [1, 0, 2]

回复：n 个数字

response = [0, 1, 2]

奖励应该捕捉回复与排序后的接近程度。

定义一个奖励，返回回复与真实值匹配的位置数：

def sort_distance_reward(prompt: list[int], response: list[int]) -> float:
    """
    Return how close response is to ground_truth = sorted(prompt).
    In particular, compute number of positions where the response matches the ground truth.
    """
    assert len(prompt) == len(response)
    ground_truth = sorted(prompt)
    return sum(1 for x, y in zip(response, ground_truth) if x == y)

# sort_distance_reward([3, 1, 0, 2], [0, 1, 2, 3]) -> 4 (全对)
# sort_distance_reward([3, 1, 0, 2], [0, 3, 1, 2]) -> 1 (只有 0 在对的位置)

定义一个替代奖励，给予更多部分分：

def sort_inclusion_ordering_reward(prompt: list[int], response: list[int]) -> float:
    """
    Return how close response is to ground_truth = sorted(prompt).
    """
    assert len(prompt) == len(response)

    # 为回复中出现的每个提示词中的 token 给 1 分
    inclusion_reward = sum(1 for x in prompt if x in response)

    # 为回复中每个排序正确的相邻对给 1 分
    ordering_reward = sum(1 for x, y in zip(response, response[1:]) if x <= y)

    return inclusion_reward + ordering_reward

# sort_inclusion_ordering_reward([3, 1, 0, 2], [0, 3, 1, 2]) -> 4 (包含) + 2 (0<3, 1<2) = 6

注意第二个奖励函数比第一个奖励函数给第三个回复提供了更多分数。

简单模型 (Simple model)

定义一个简单的模型，将提示词映射到回复 * 假设固定的提示词和回复长度 * 使用单独的每位置参数捕捉位置信息 * 独立解码回复中的每个位置（非自回归）

class Model(nn.Module):
    def __init__(self, vocab_size: int, embedding_dim: int, prompt_length: int, response_length: int):
        super().__init__()
        self.embedding_dim = embedding_dim
        self.embedding = nn.Embedding(vocab_size, embedding_dim)
        # For each position, we have a matrix for encoding and a matrix for decoding
        self.encode_weights = nn.Parameter(torch.randn(prompt_length, embedding_dim, embedding_dim) / math.sqrt(embedding_dim))
        self.decode_weights = nn.Parameter(torch.randn(response_length, embedding_dim, embedding_dim) / math.sqrt(embedding_dim))

    def forward(self, prompts: torch.Tensor) -> torch.Tensor:
        """
        Args:
            prompts: int[batch pos]
        Returns:
            logits: float[batch pos vocab]
        """
        # Embed the prompts
        embeddings = self.embedding(prompts)   # [batch pos dim]

        # Transform using per prompt position matrix, collapse into one vector
        encoded = einsum(embeddings, self.encode_weights, "batch pos dim1, pos dim1 dim2 -> batch dim2")

        # Turn into one vector per response position
        decoded = einsum(encoded, self.decode_weights, "batch dim2, pos dim2 dim1 -> batch pos dim1")

        # Convert to logits (input and output share embeddings)
        logits = einsum(decoded, self.embedding.weight, "batch pos dim1, vocab dim1 -> batch pos vocab")

        return logits

GRPO 算法流程详解

让我们通过详细的代码来看看 GRPO 算法的每一步：

1. 从提示词 s 开始

   prompts = torch.tensor([[1, 0, 2]])  # [batch pos]
   

2. 生成回复 a 我们对于一个提示词需要采样多个回复 (group)。

   def generate_responses(prompts: torch.Tensor, model: Model, num_responses: int) -> torch.Tensor:
       logits = model(prompts)  # [batch pos vocab]
       batch_size = prompts.shape[0]
   
       # Sample num_responses (independently) for each [batch pos]
       flattened_logits = rearrange(logits, "batch pos vocab -> (batch pos) vocab")
       flattened_responses = torch.multinomial(softmax(flattened_logits, dim=-1), num_samples=num_responses, replacement=True)  # [batch pos trial]
       responses = rearrange(flattened_responses, "(batch pos) trial -> batch trial pos", batch=batch_size)
       return responses
   
   responses = generate_responses(prompts=prompts, model=model, num_responses=5)
   

3. 计算这些回复的奖励 R

   rewards = compute_reward(prompts=prompts, responses=responses, reward_fn=sort_inclusion_ordering_reward)
   

4. 给定奖励 R 计算 deltas δ（用于执行更新）： 这里是 GRPO 核心创新的地方：如何计算 advantage (delta)。

   def compute_deltas(rewards: torch.Tensor, mode: str) -> torch.Tensor:
       if mode == "rewards":
           return rewards
   
       if mode == "centered_rewards":
           # Compute mean over all the responses (trial) for each prompt (batch)
           mean_rewards = rewards.mean(dim=-1, keepdim=True)
           centered_rewards = rewards - mean_rewards
           return centered_rewards
   
       if mode == "normalized_rewards":
           mean_rewards = rewards.mean(dim=-1, keepdim=True)
           std_rewards = rewards.std(dim=-1, keepdim=True)
           centered_rewards = rewards - mean_rewards
           normalized_rewards = centered_rewards / (std_rewards + 1e-5)
           return normalized_rewards
   
       if mode == "max_rewards":
           # Zero out any reward that isn't the maximum for each batch
           max_rewards = rewards.max(dim=-1, keepdim=True)[0]
           max_rewards = torch.where(rewards == max_rewards, rewards, torch.zeros_like(rewards))
           return max_rewards
   
       raise ValueError(f"Unknown mode: {mode}")
   

5. 计算这些回复的对数概率 我们需要计算模型在这些回复上的 log probability。

   def compute_log_probs(prompts: torch.Tensor, responses: torch.Tensor, model: Model) -> torch.Tensor:
       # Compute log prob of responses under model
       logits = model(prompts)  # [batch pos vocab]
       log_probs = F.log_softmax(logits, dim=-1)  # [batch pos vocab]
   
       # Replicate to align with responses
       num_responses = responses.shape[1]
       log_probs = repeat(log_probs, "batch pos vocab -> batch trial pos vocab", trial=num_responses)
   
       # Index into log_probs using responses
       log_probs = log_probs.gather(dim=-1, index=responses.unsqueeze(-1)).squeeze(-1)  # [batch trial pos]
   
       return log_probs
   
   log_probs = compute_log_probs(prompts=prompts, responses=responses, model=model)
   

   重要：冻结参数注意事项。 在优化时，重要的是冻结并不对 p_old 进行微分。

   def freezing_parameters():
       # ... demonstration ...
       with torch.no_grad():  # Important: treat p_old as a constant!
            p_old = torch.nn.Sigmoid()(w)
       # ...
   

6. 计算损失以更新模型参数 我们有多种计算损失的方式：

   • Naive: 直接使用 log_probs * deltas
   • Unclipped: 引入重要性采样比率 ratios
   • Clipped (PPO style): 截断比率以保证更新幅度受控

   def compute_loss(log_probs: torch.Tensor, deltas: torch.Tensor, mode: str, old_log_probs: torch.Tensor | None = None) -> torch.Tensor:
       if mode == "naive":
           return -einsum(log_probs, deltas, "batch trial pos, batch trial -> batch trial pos").mean()
   
       if mode == "unclipped":
           ratios = log_probs / old_log_probs  # [batch trial]
           return -einsum(ratios, deltas, "batch trial pos, batch trial -> batch trial pos").mean()
   
       if mode == "clipped":
           epsilon = 0.01
           unclipped_ratios = log_probs / old_log_probs  # [batch trial]
           unclipped = einsum(unclipped_ratios, deltas, "batch trial pos, batch trial -> batch trial pos")
   
           clipped_ratios = torch.clamp(unclipped_ratios, min=1 - epsilon, max=1 + epsilon)
           clipped = einsum(clipped_ratios, deltas, "batch trial pos, batch trial -> batch trial pos")
           return -torch.minimum(unclipped, clipped).mean()
   
       raise ValueError(f"Unknown mode: {mode}")
   

7. KL 惩罚 (KL penalty) 有时，我们可以使用显式的 KL 惩罚来正则化模型。 如果你想让 RL 为模型增加新能力，但不希望它忘记原有能力，这很有用。

   def compute_kl_penalty(log_probs: torch.Tensor, ref_log_probs: torch.Tensor) -> torch.Tensor:
       """
       Compute an estimate of KL(model | ref_model)
       Scale using estimate: KL(p || q) = E_p[q/p - log(q/p) - 1]
       """
       return (torch.exp(ref_log_probs - log_probs) - (ref_log_probs - log_probs) - 1).sum(dim=-1).mean()
   

实验 (Experiments)

1. 基于原始奖励 (Raw Rewards) 更新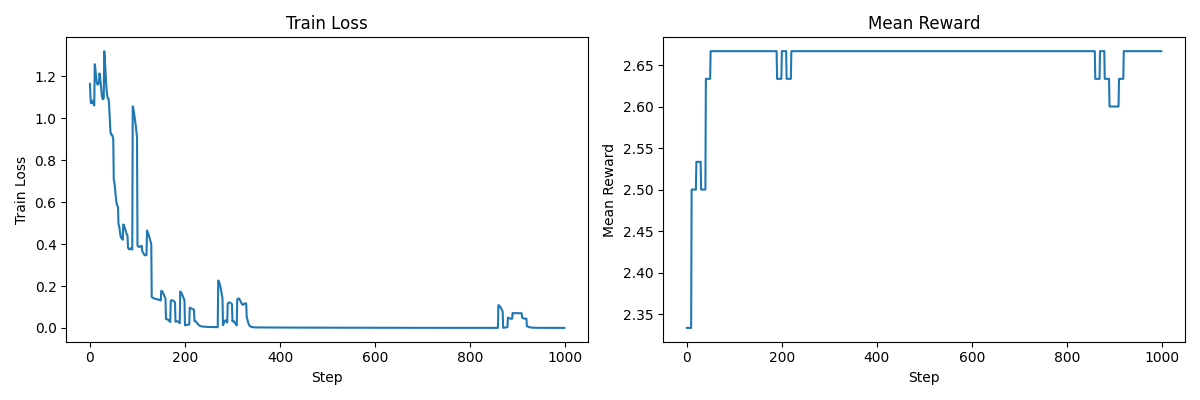 通过查看输出，你会发现到最后，我们并没有真正学好排序（而且这还是训练集）。

2. 使用中心化奖励 (Centered Rewards)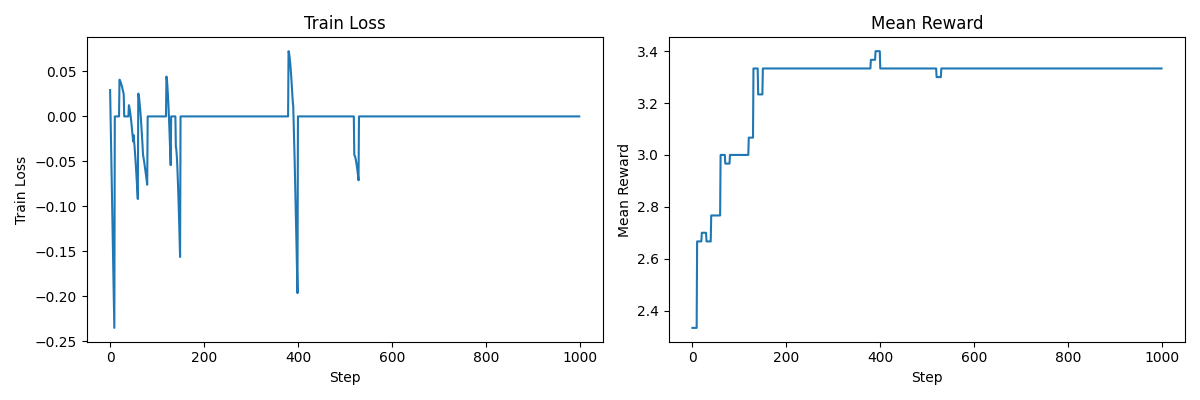 这似乎有所帮助，因为： * 次优奖励会得到负梯度更新 * 如果给定提示词的所有回复都具有相同的奖励，则我们不更新。 总体而言，这更好，但我们仍然陷入局部最优。

3. 使用标准差归一化 (Normalized Rewards)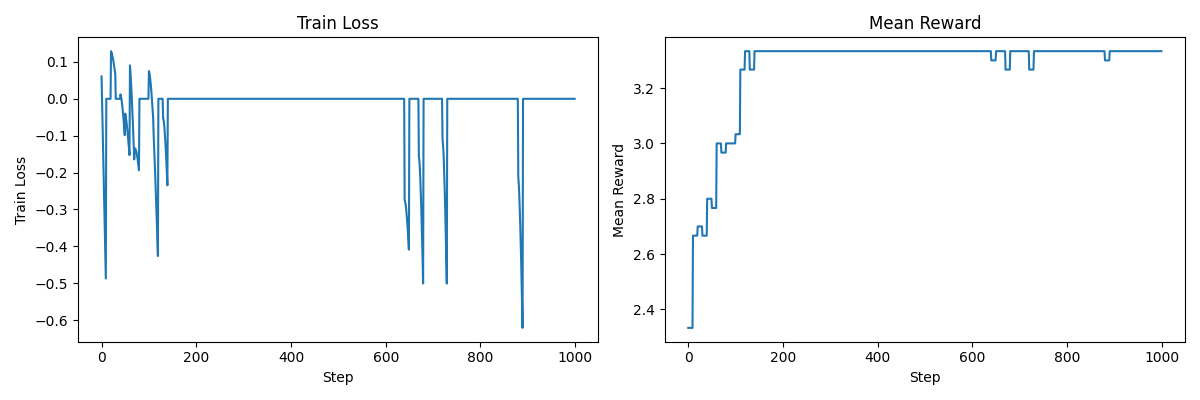 这里差别不大，实际上，像 Dr. GRPO 这样的变体不执行这种归一化以避免长度偏差（这里不是问题，因为所有回复长度相同）。Link

总的来说，正如你所见，强化学习并非易事，很容易陷入次优状态。 超参数可能需要更好的调整...

4. 总结 (Summary)

• 强化学习是超越人类能力的关键
• 如果你能衡量它，你就能优化它
• 策略梯度框架概念清晰，只需要基线来减少方差
• RL 系统比预训练复杂得多（推理工作负载，管理多个模型）

接下来的两讲： * Junyang Lin (Qwen) Link * Mike Lewis (Llama) Link

---

💬 评论