大模型从0到1｜第十一讲：如何用好 Scaling Law (Scaling - Case Study and Details)

课程链接：Stanford CS336 Spring 2025 - Lecture 11

课程信息

• 课程: CS336
• 讲师: Tatsu H
• 主题: 深入探讨 Scaling Law 在实际工程中的应用，包括 muP 参数化、WSD 学习率调度以及 Chinchilla 定律的拟合细节。

---

Part 1: 课程背景与动机 (Motivation)

Page 1: 标题页

• 内容: Lecture 11: Scaling - Case Study and Details。
• 解析: 本节课的主题是“扩展定律的案例研究与细节”。既然我们知道了 Scaling Law 的存在，那么在实际操作中（In the wild），我们该如何具体执行？

Page 2: 核心动机 (Motivation Today)

• 关键问题:
  1. Chinchilla 有效吗？ DeepMind 的扩展方法在实际操作中真的管用吗？
  2. 省钱: 我们能否在训练和拟合 Scaling Law 时节省算力？（拟合曲线本身就很贵）。
  3. 架构选择: 为了更好的扩展性，我们需要选择特定的架构或参数化方式吗？

Page 3: 扩展实战案例概览

• 时间线:
  • 2022: DeepMind (Chinchilla) —— 提出了计算最优（Compute-optimal）的概念。
  • 2023: Cerebras-GPT —— 验证了在特定硬件上复现 Chinchilla 规律。
  • 2024: DeepSeek, MiniCPM, Llama 3, Hunyuan-Large —— 这一年爆发了多种 Scaling 策略。
  • 2025: MiniMax-01 —— 最新的探索。

---

Part 2: 案例一 - Cerebras-GPT 与 muP

Page 4: Cerebras-GPT 概览

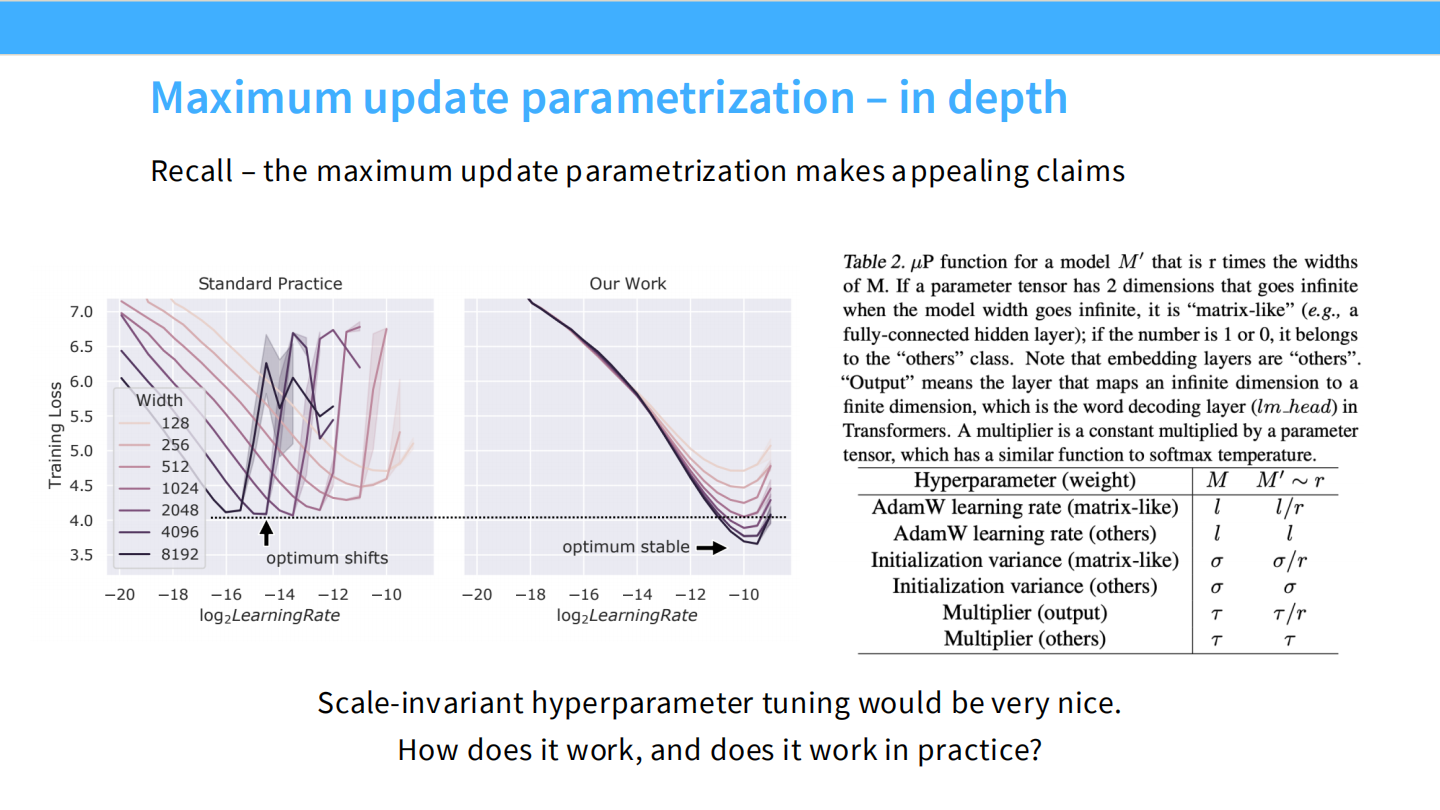
• 背景: Cerebras 发布了一系列从 111M 到 13B 的模型，严格遵循 Chinchilla 的配方。
• 验证: 图表显示，Cerebras-GPT 的 Validation Loss 完美地落在了一条幂律曲线上（虚线）。这证明了 Scaling Law 在不同硬件架构上的普适性。

Page 5: 超参数扩展策略

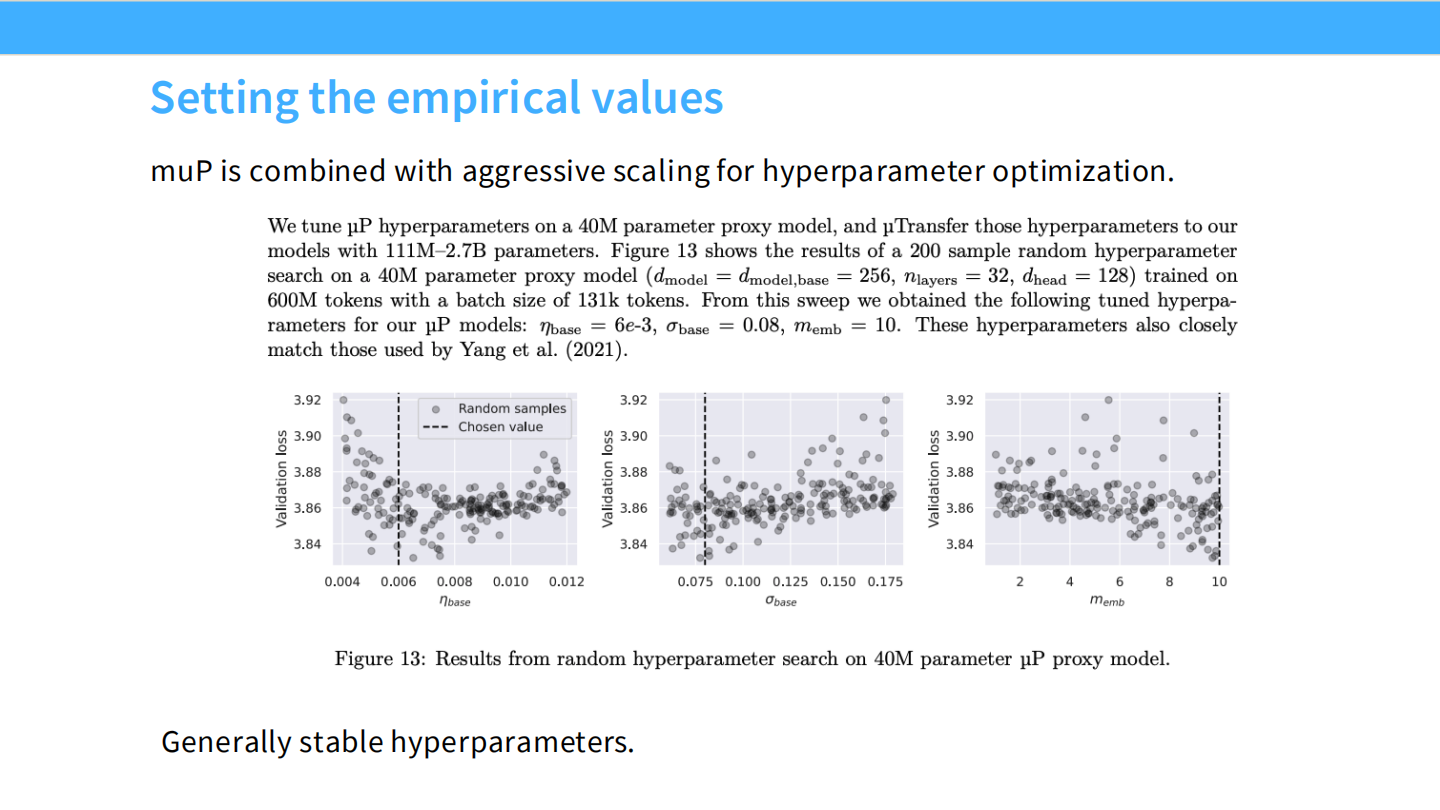
• 图表: 展示了 Cerebras-GPT 实际上是如何预测超参数的。
• 发现: 随着模型变大（Training FLOPS 增加），最佳的学习率（Learning Rate）并不是恒定的，也不是随意设定的，而是遵循某种规律。Cerebras 作者发现使用 muP (Maximal Update Parametrization) 可以让这种规律变得非常可预测。

Page 6: muP 参数化 (muP Parametrization)

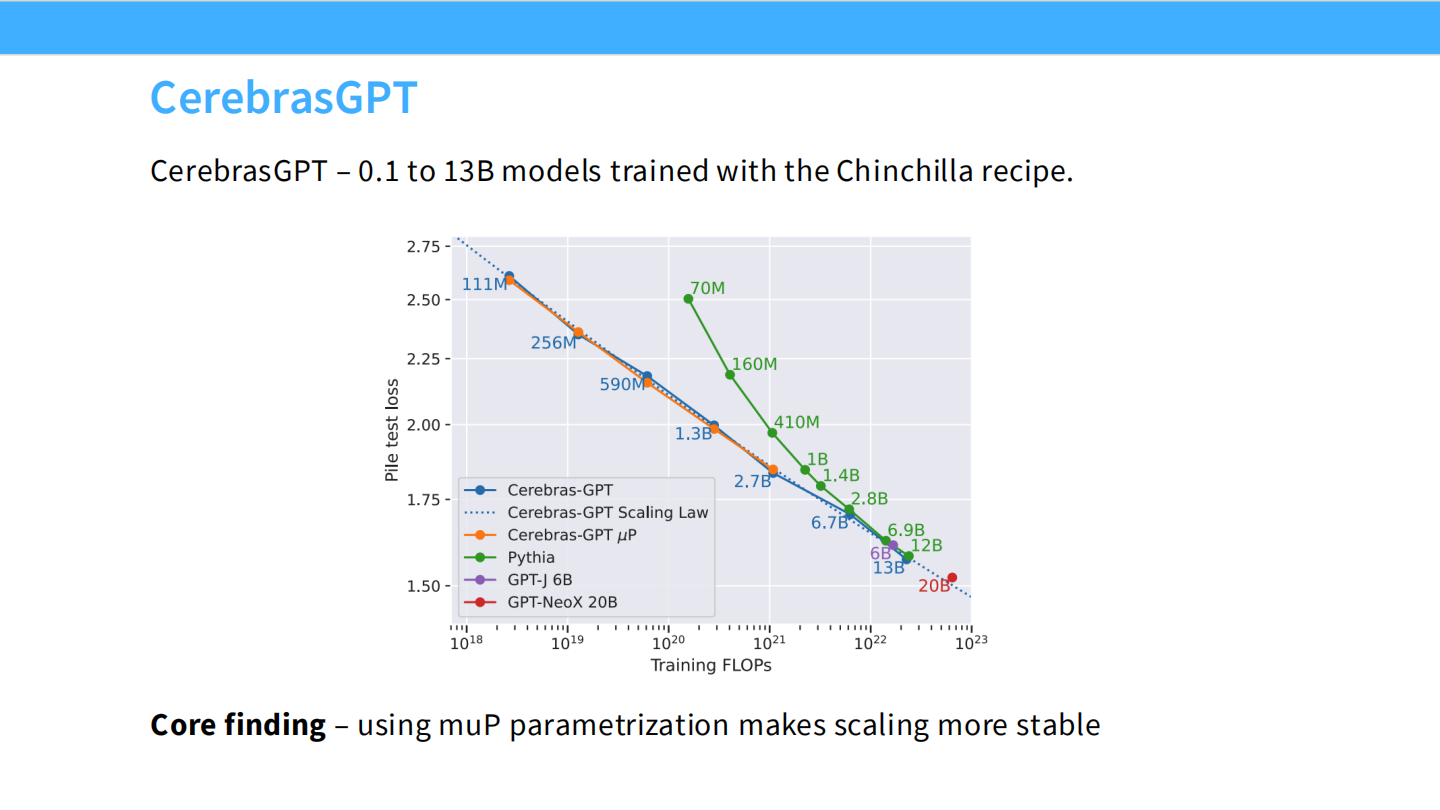
• 表格: 附录中展示了标准参数化（Standard Parameterization, SP）与 muP 的具体区别。
• 关键差异:
  • Embedding: muP 的初始化方差和 LR 都是常数（1）。
  • Attention/MLP: muP 的初始化方差是 $1/Width$，LR 是 $1/Width$。
  • Output Layer: muP 的初始化方差是 $1/Width^2$。
  • Attention Scaling: muP 使用 $1/D$ 而不是 $1/\sqrt{D}$。

Page 7: 经验值设定

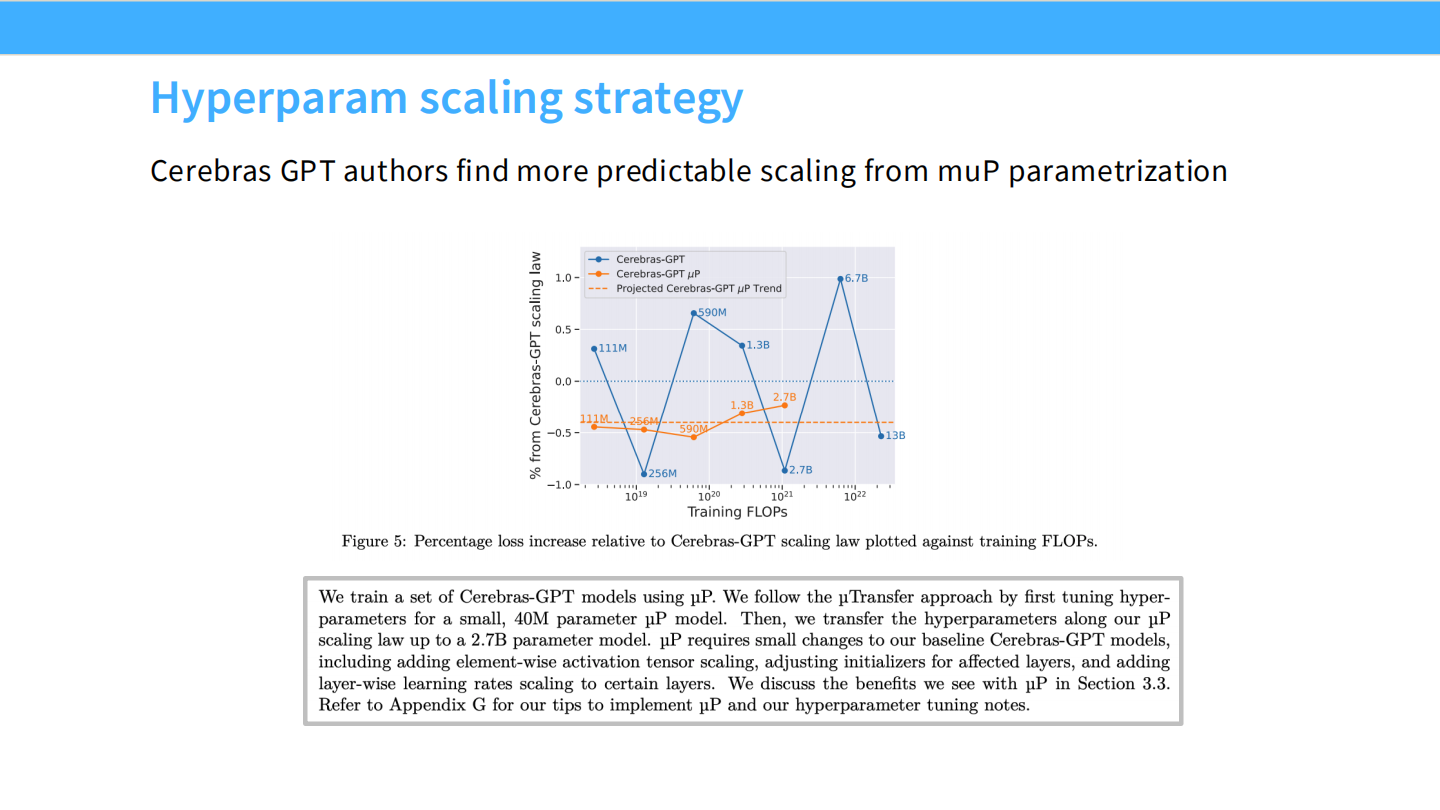
• 方法:
  1. 在一个小模型（40M 参数）上进行随机超参数搜索（Grid Search）。
  2. 找到最佳的 LR 和 Init Std。
  3. 利用 muP 的规则，直接将这些参数迁移到大模型上。
• 图表: 展示了小模型上 Loss 对 LR 和 Init Std 的敏感度。

Page 8: 什么是 muP? (原理)

• 论文: “A Spectral Condition for Feature Learning”。
• 核心思想: 随着网络宽度 $n_l$ 趋向无穷大，我们需要满足两个条件以保持训练稳定：
  1. A1 (Activation): 初始化时的激活值应保持 $O(1)$。
  2. A2 (Update): 经过一次梯度更新后，激活值的变化量应保持 $O(1)$。

Page 9: 推导 muP (条件 A1)

• 场景: 简单的深度线性网络 $h_l = W_l h_{l-1}$。
• 推导: 如果 $W_l \sim N(0, \sigma^2)$，为了让输出范数不随宽度 $n_l$ 爆炸，我们需要设置方差 $\sigma \approx 1/\sqrt{n_l}$。这与 Xavier 初始化一致。

Page 10: 推导 muP (条件 A2)

• 场景: 考虑权重更新 $\Delta W_l = -\eta \nabla \ell$。
• 推导: 更新后的激活值变化 $\Delta h_l = W_l \Delta h_{l-1} + \Delta W_l h_{l-1}$。我们希望这一项也是 $O(\sqrt{n_l})$（与激活值同级）。

Page 11: 推导 muP (条件 A2) Part 2

• 结论: 为了满足上述条件，学习率 $\eta$ 必须随着宽度 $n_l$ 的增加而减小，具体来说 $\eta_l = \Theta(1/n_{l-1})$。
• 意义: 这就是为什么在大模型训练中，通常模型越宽，学习率越小的理论依据。

Page 12: muP 小结

• 总结: muP 是一套关于初始化和学习率的缩放规则（作为宽度的函数）。
  • Initialization: $\Theta(1/\sqrt{n})$
  • Learning Rate: $\Theta(1/n)$ (对于 Adam)
• 对比: 标准参数化（Standard）通常只做初始化缩放，而忽略了 LR 的缩放。

Page 13: Cerebras-GPT 实现细节

• 表格: 展示了具体的实现值。
  • Attention Scale 使用 $1/D$（通常是 $1/\sqrt{D}$）。这一改变在宽度增加时尤为重要。

Page 14: muP 的更深层细节

• 表格: 详细列出了每一类参数（Embedding, Attention, MLP, Logits）的初始化方差和学习率缩放规则。
• 注意: Embedding 层和 Output 层通常有特殊的缩放规则（如 $1/M$ vs $1/M^2$），以保证输入输出的稳定性。

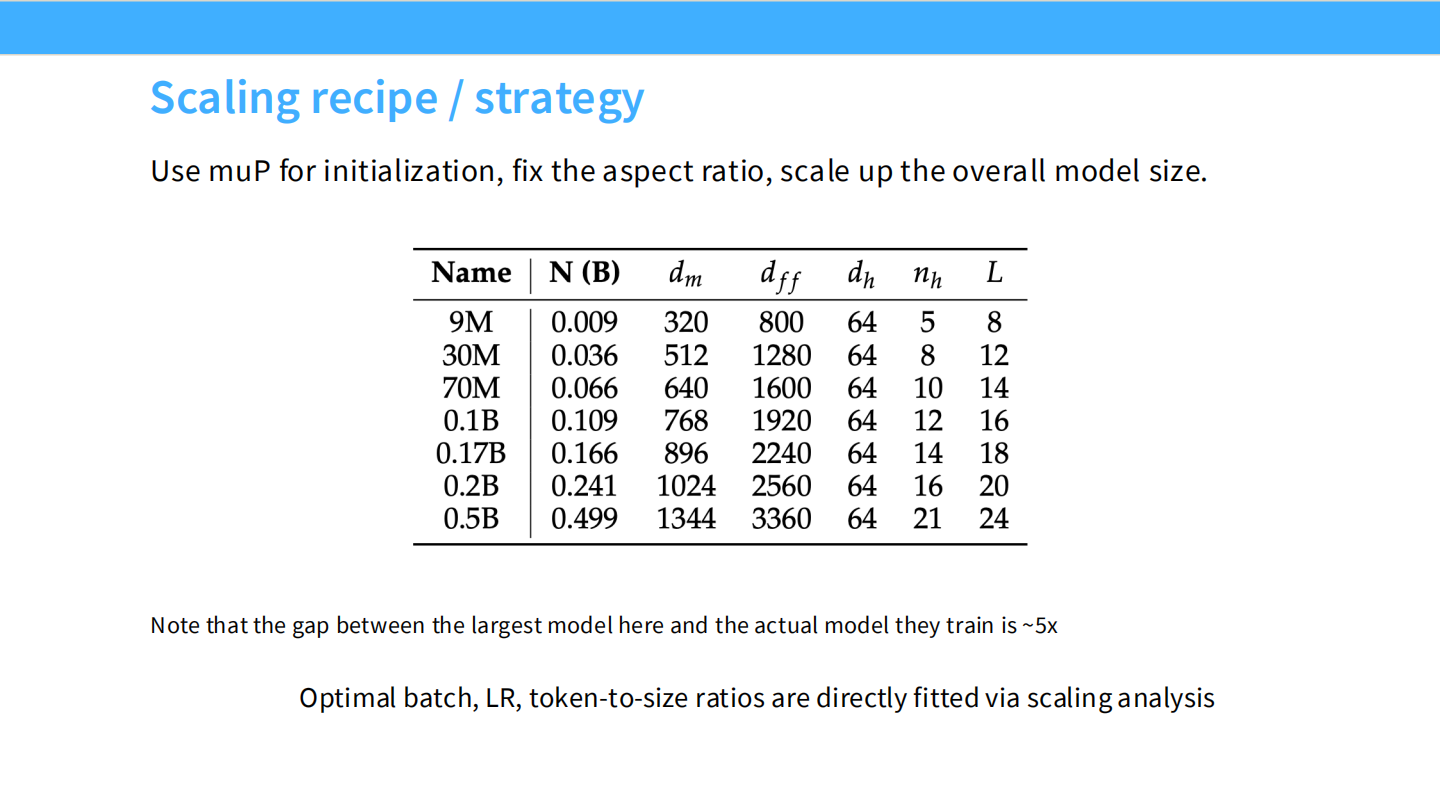
Page 15: 扩展协议 (Scaling Protocol)

• 表格: Cerebras-GPT 训练的模型列表。
• 局限性: 该工作只探索了宽度 (Width) 的扩展，深度相对固定。这是 muP 理论目前主要覆盖的领域。

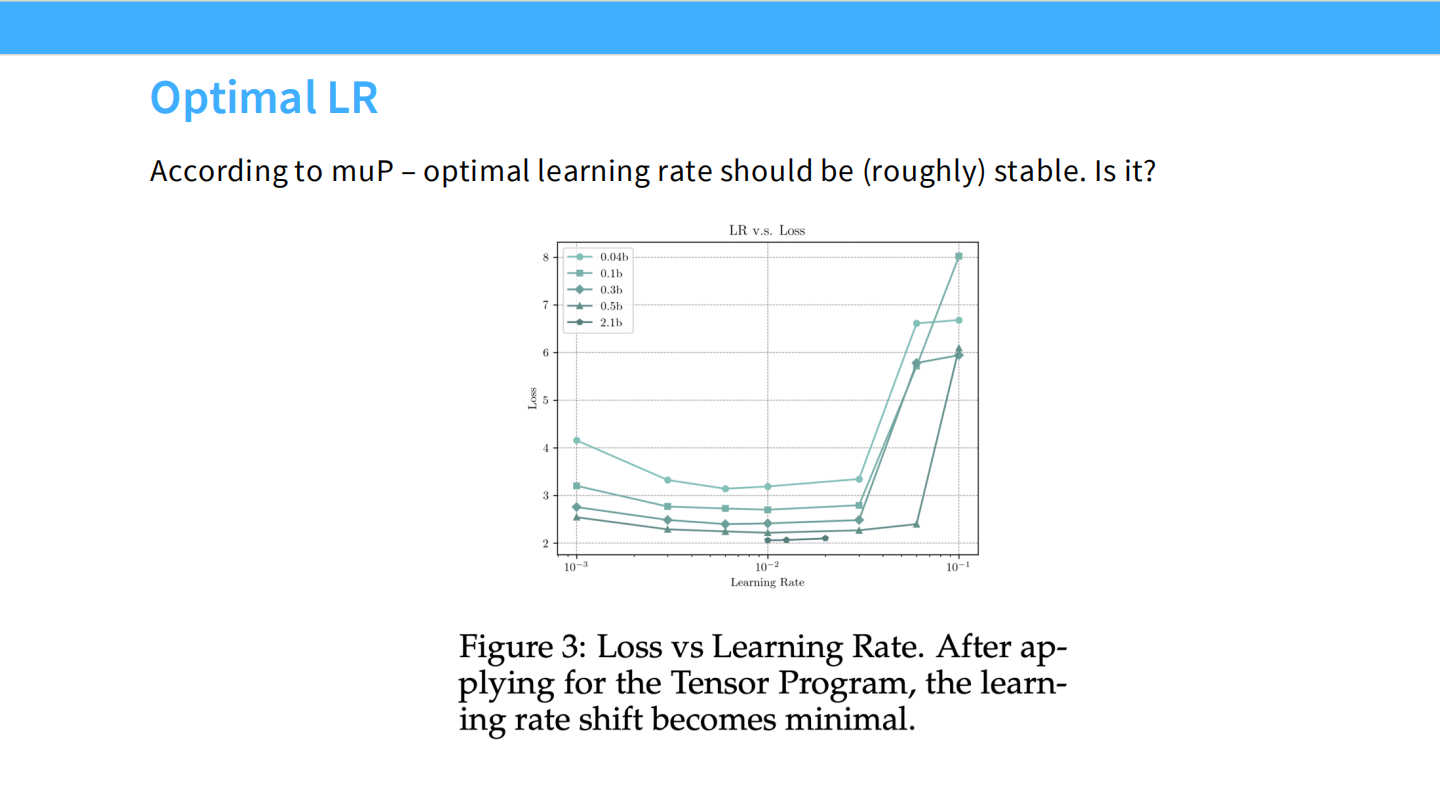
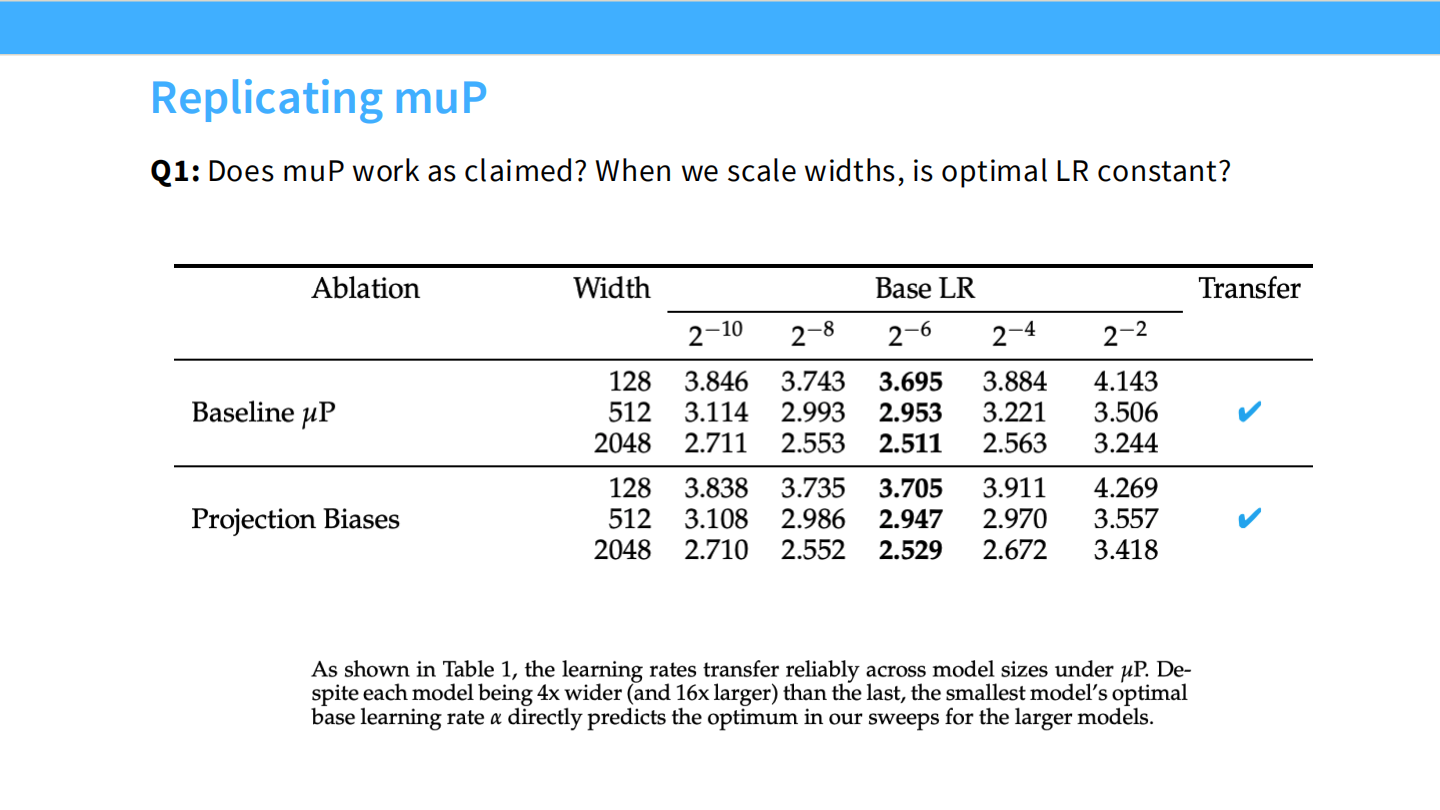
Page 16: 验证 muP (Replicating muP)

• 问题: muP 真的像宣称的那样有效吗？即“最佳学习率是常数”？
• 验证: 表格显示，在 Baseline (SP) 下，随着宽度从 128 到 2048，最佳 LR 从 3.695 降到了 2.511。但在 muP 下，最佳 Base LR 稳定在 3.7 左右。验证成功。

Page 17: muP 的鲁棒性 (Robustness)

• 背景: 现代 LLM 有很多组件（如 SwiGLU, RMSNorm）并不在 muP 最初的理论假设中。muP 还能用吗？
• 列表:
  • SwiGLU / Squared ReLU: 鲁棒。
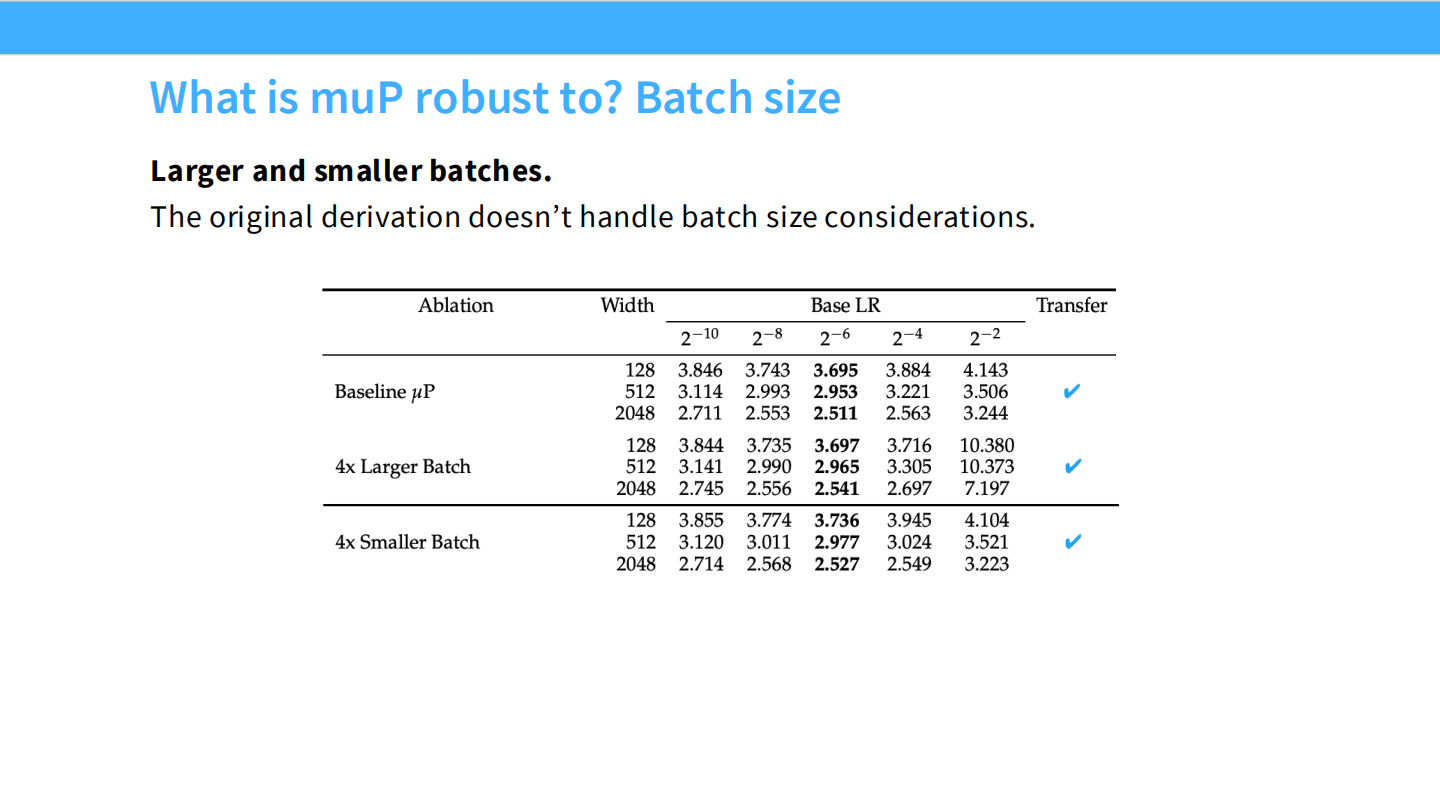
  • Batch Size: 鲁棒。
  • Initialization (Zero Query): 鲁棒。
  • RMSNorm Gains: **不鲁棒 (Break)**。
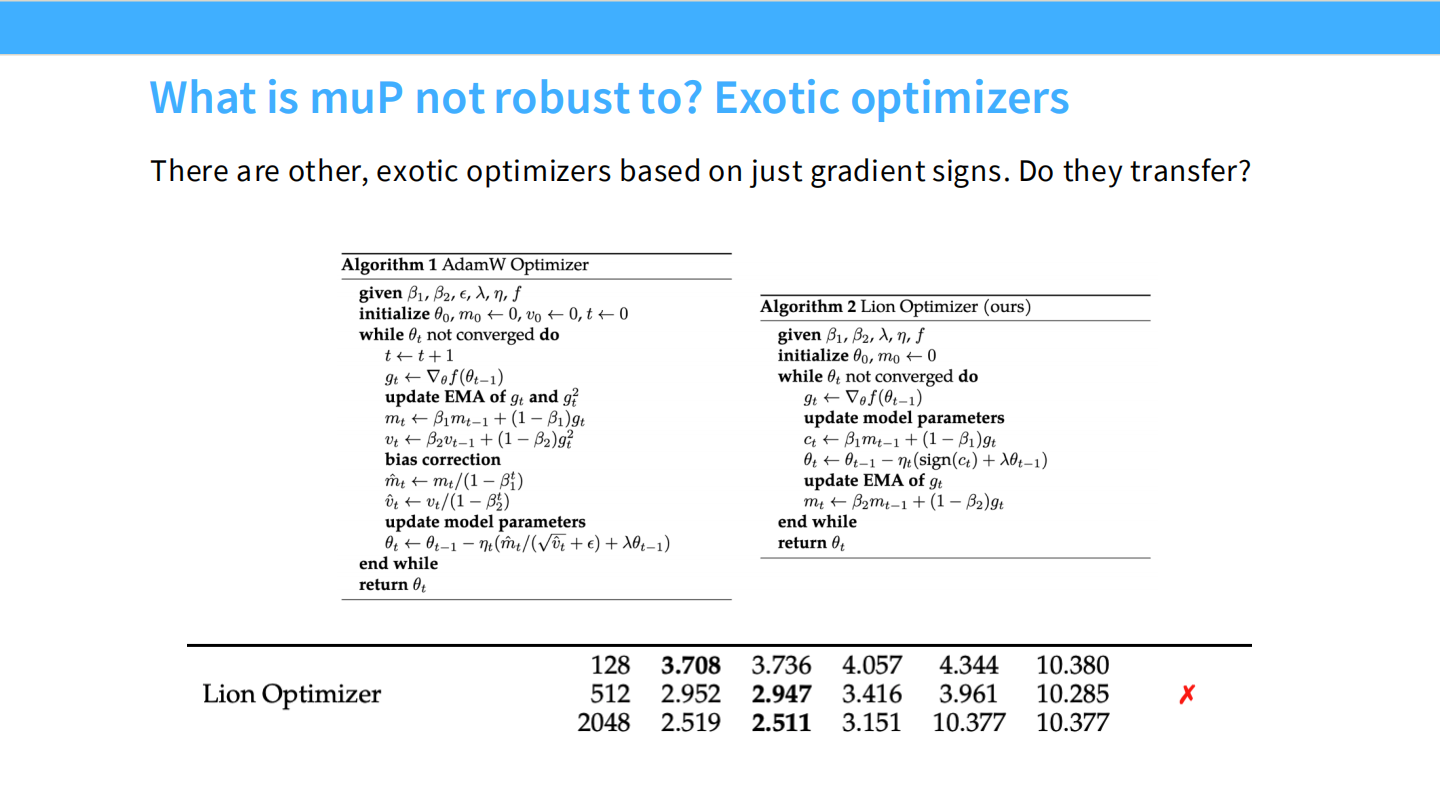
  • Lion Optimizer: 不鲁棒。
  • Weight Decay: 不鲁棒。

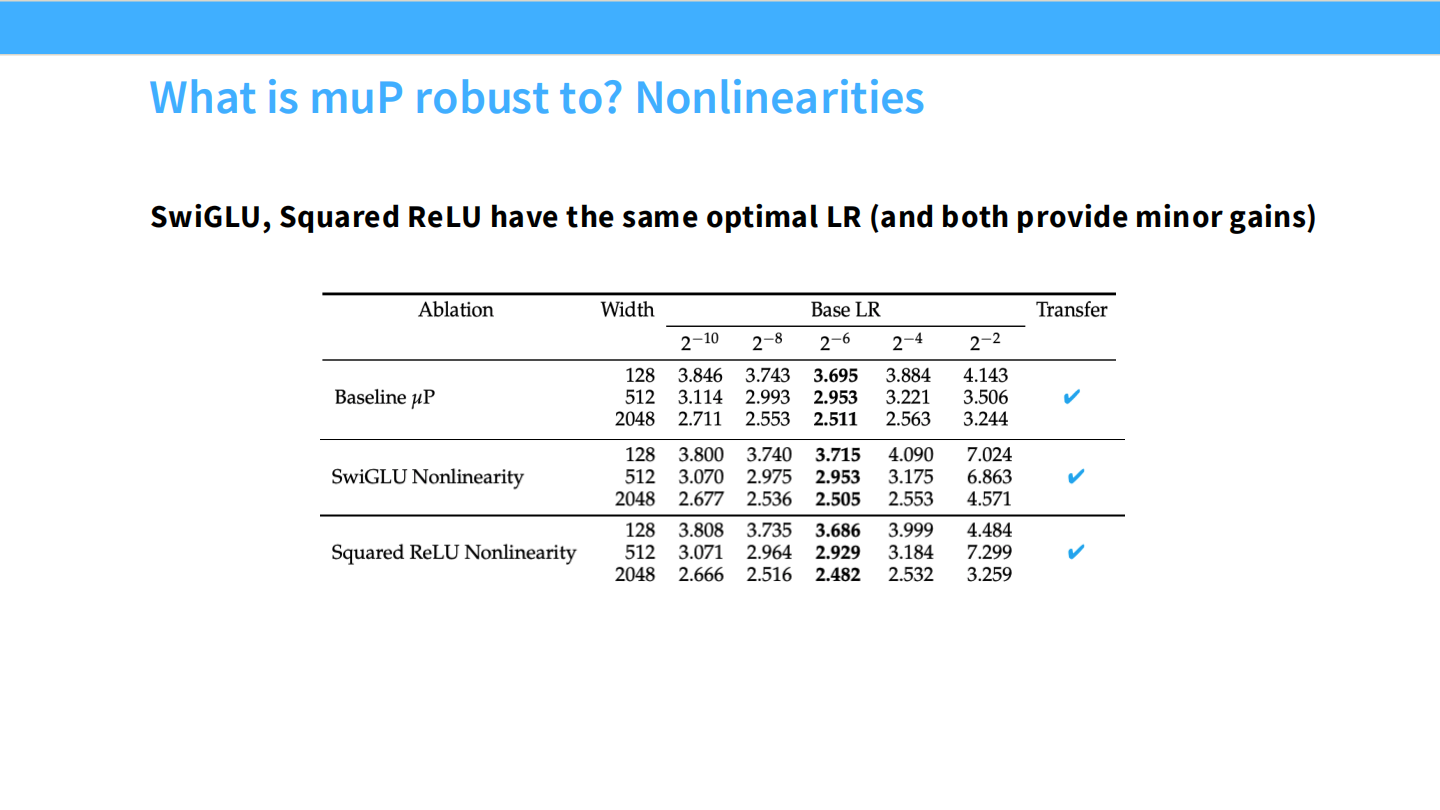
Page 18: 鲁棒性 - 非线性激活

• 结论: 无论是 SwiGLU 还是 Squared ReLU，muP 都能保持最佳 LR 的稳定性。

Page 19: 鲁棒性 - Batch Size

• 结论: Batch Size 的变化不影响 muP 的 LR 迁移规律。虽然原始推导没考虑 Batch Size，但经验上是兼容的。

Page 20: 鲁棒性 - 初始化

• 结论: 使用 Zero Query Init（将 Query 初始化为 0）等技巧也不影响 muP。

Page 21: 不鲁棒 - RMSNorm Gain

• 现象: 如果 RMSNorm 带有可学习的增益参数（Gain $\gamma$），muP 失效。
• 解决方案: 直接移除 RMSNorm 的可学习参数（Fix $\gamma=1$）。这几乎不影响性能，但恢复了 muP 的特性。

Page 22: 不鲁棒 - 异构优化器 (Lion)

• 现象: Lion 优化器基于符号（Sign），不符合 muP 的假设。无法直接迁移。

Page 23: 不鲁棒 - 强权重衰减

• 现象: 当 Weight Decay 设为 0.1（现代标准）时，muP 失效。这是一个主要短板。

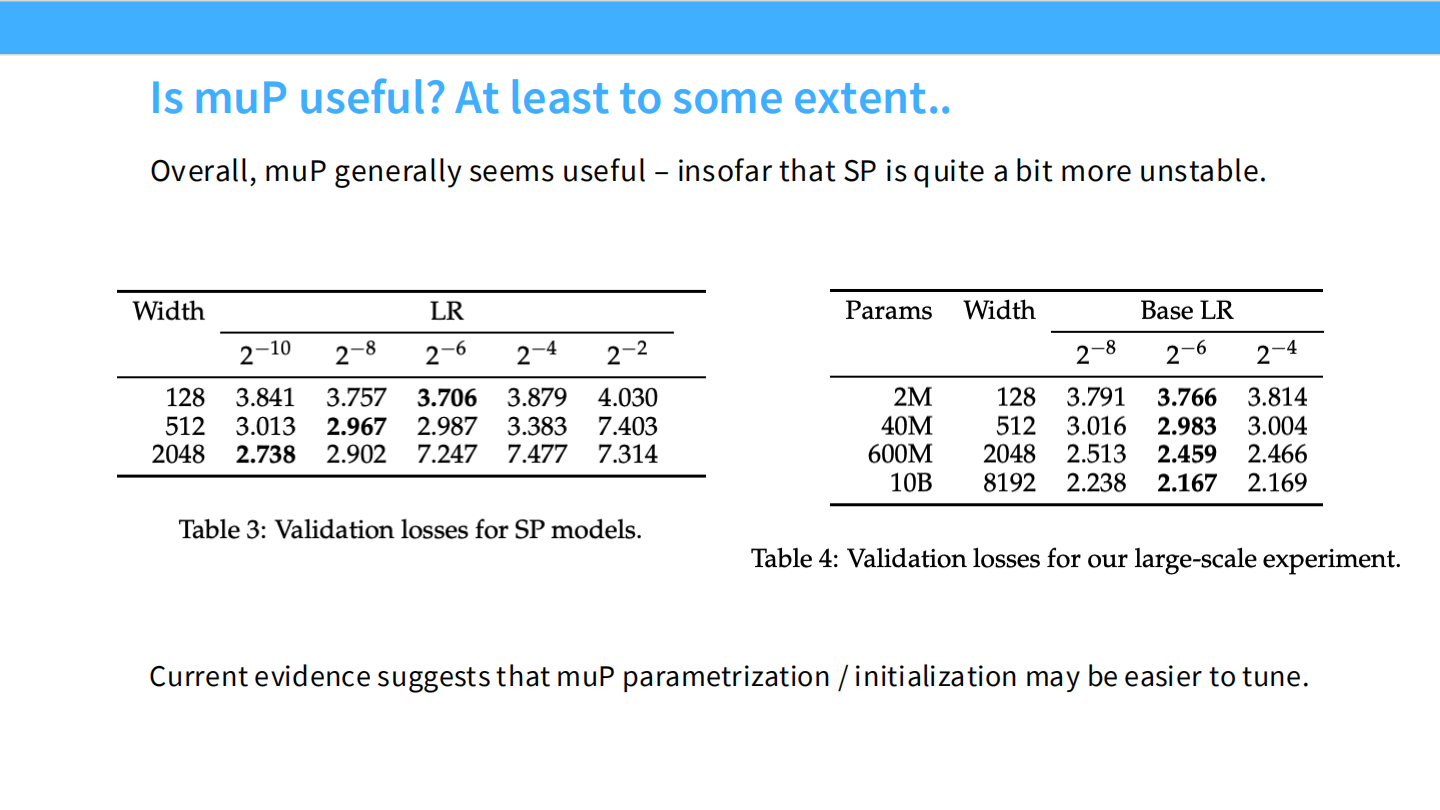
Page 24: muP 总结

• 有用吗？ 总体非常有用。特别是对于 SP（标准参数化）不稳定的场景。
• 建议: 如果从头训练，使用 muP 初始化和参数化可以节省大量的调参时间。

---

Part 3: 案例二 - MiniCPM 与 WSD 调度

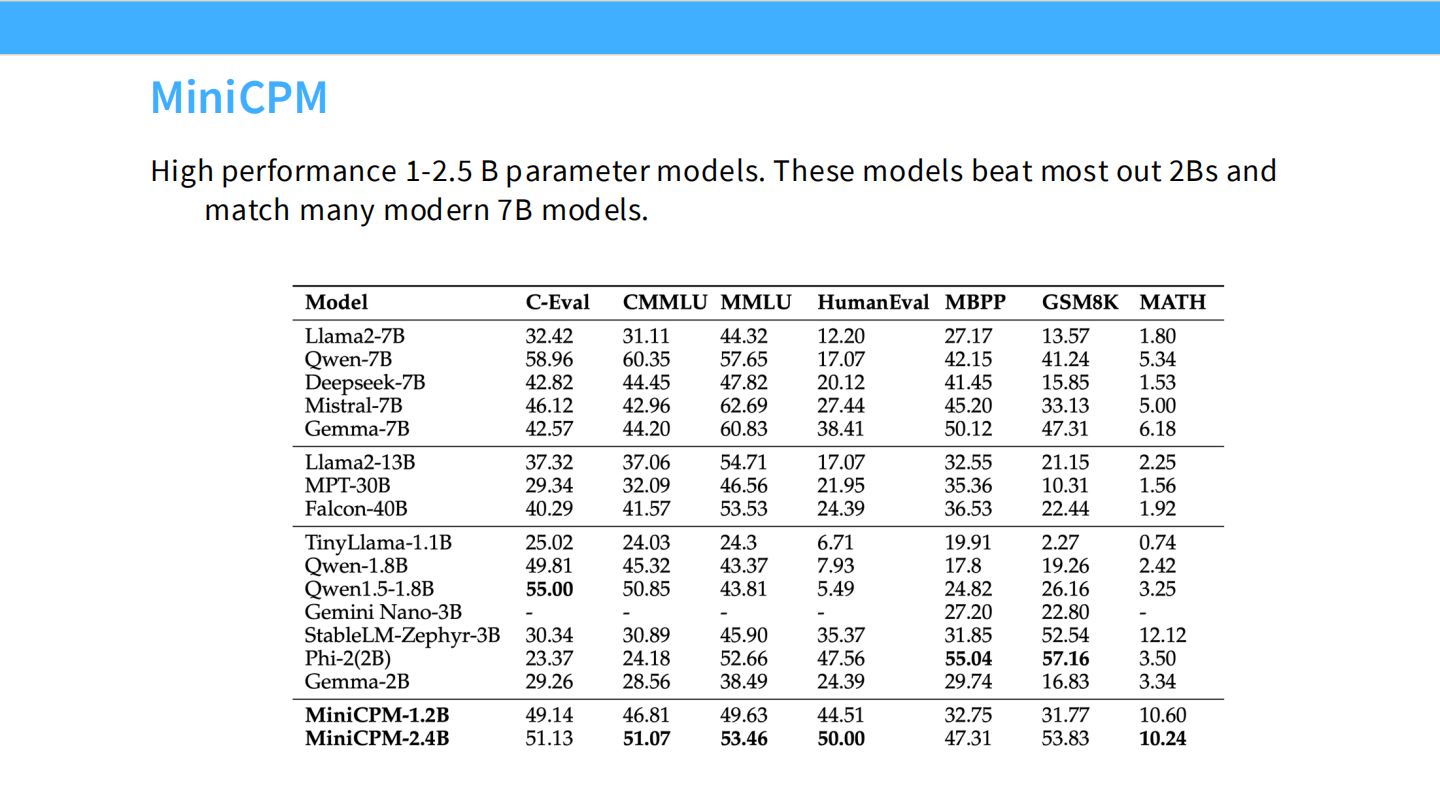
Page 25: MiniCPM 介绍

• 背景: 清华团队发布的 2.4B 小模型。性能极强。
• 特点: 他们公开了详细的“可扩展训练策略”。

Page 26: MiniCPM 的扩展配方

• 核心:
  1. 使用 muP 来稳定 Scaling。
  2. 使用 WSD (Warmup-Stable-Decay) 调度器。

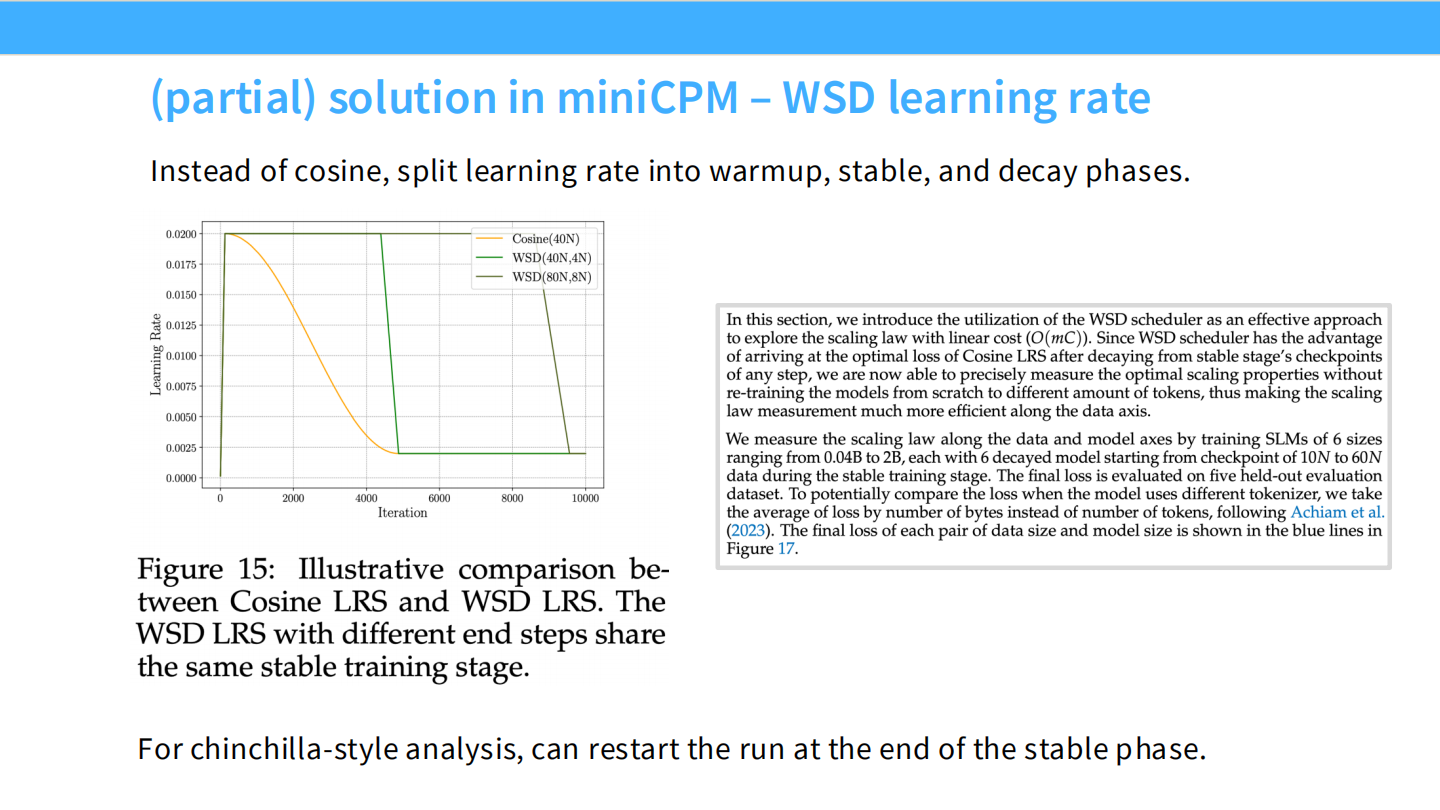
Page 27: WSD 学习率调度 (WSD Scheduler)

• 图表 (Figure 15): 对比了 Cosine 调度（黄色）和 WSD 调度（绿色）。
• WSD 阶段:
  1. Warmup: 预热。
  2. Stable: LR 保持恒定（高位）。
  3. Decay: 在训练结束前（例如最后 10% 的 Token），让 LR 急剧下降。
• 优势: 在 Stable 阶段，你可以随时决定“结束训练”。只需从当前 Checkpoint 开始做 Decay，就能得到收敛的模型。这允许一次训练测试多个数据量。

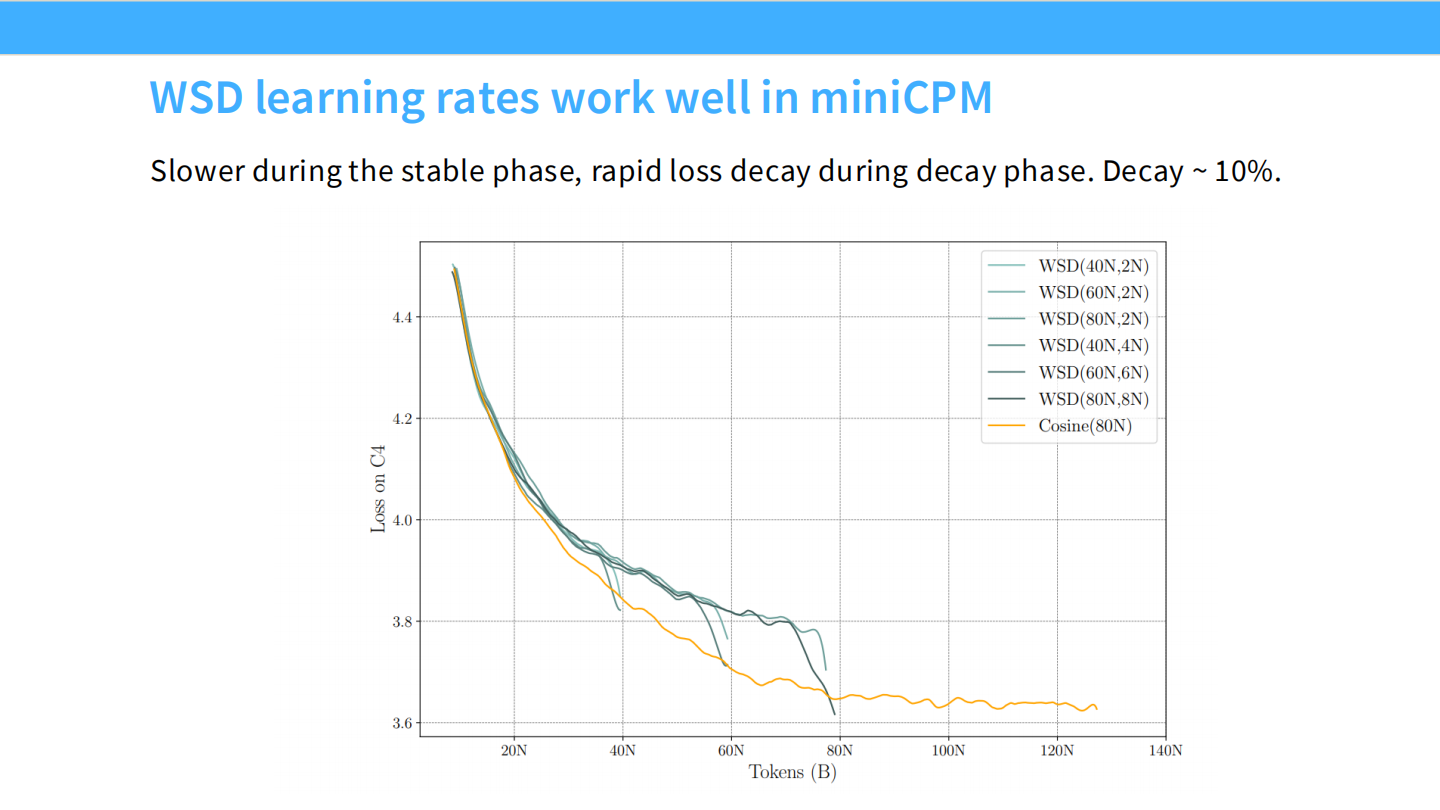
Page 28: WSD 的效果

• 图表: 展示了在 MiniCPM 训练中，LR 在 Stable 阶段保持高位，Loss 缓慢下降。一旦进入 Decay 阶段，Loss 迅速下降约 10% 并收敛。

---

Part 4: Chinchilla Scaling Law 的拟合方法

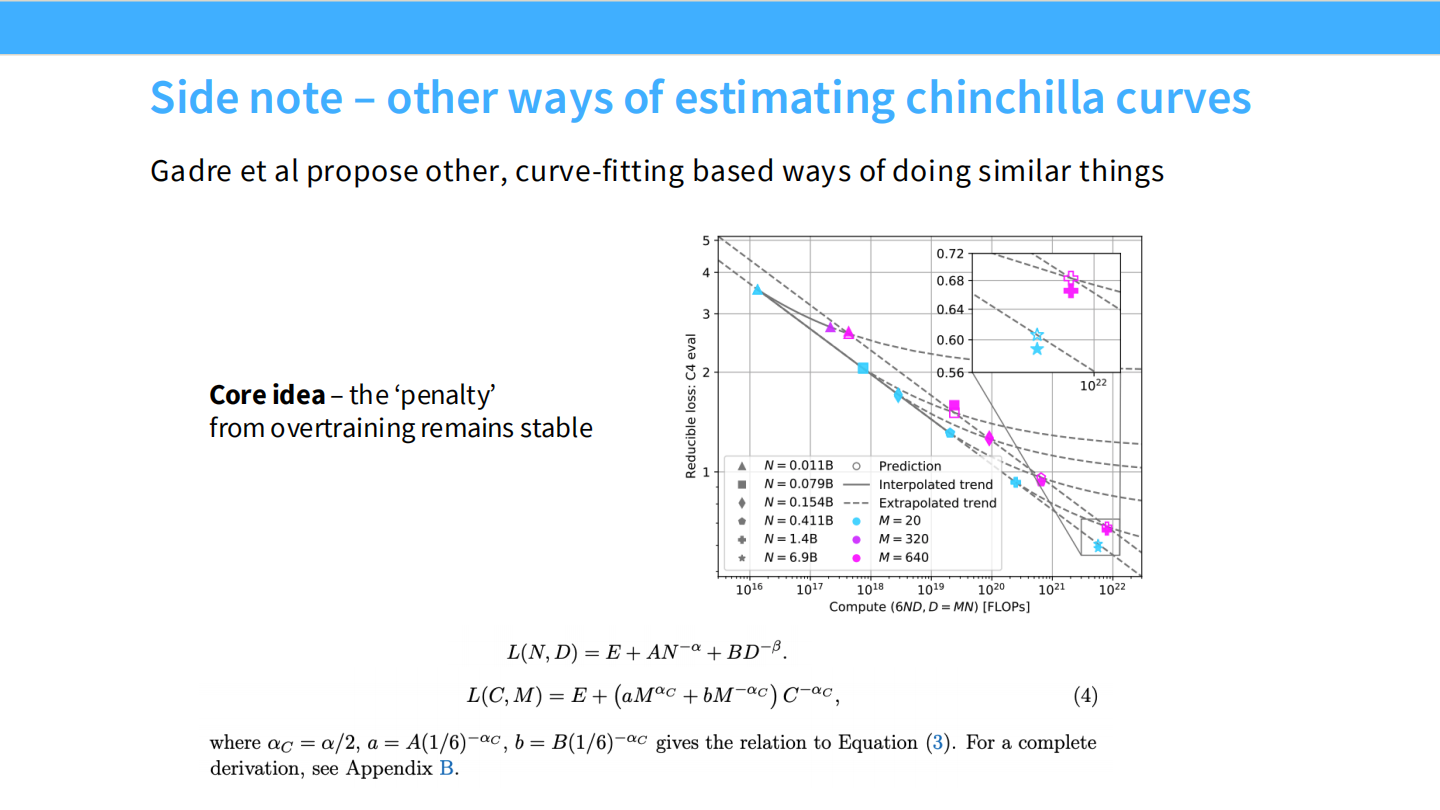
Page 29: 旁注 - 其他拟合方法

• 内容: 提到 Gadre et al 的工作。不仅看 Loss，还看“过拟合惩罚”。

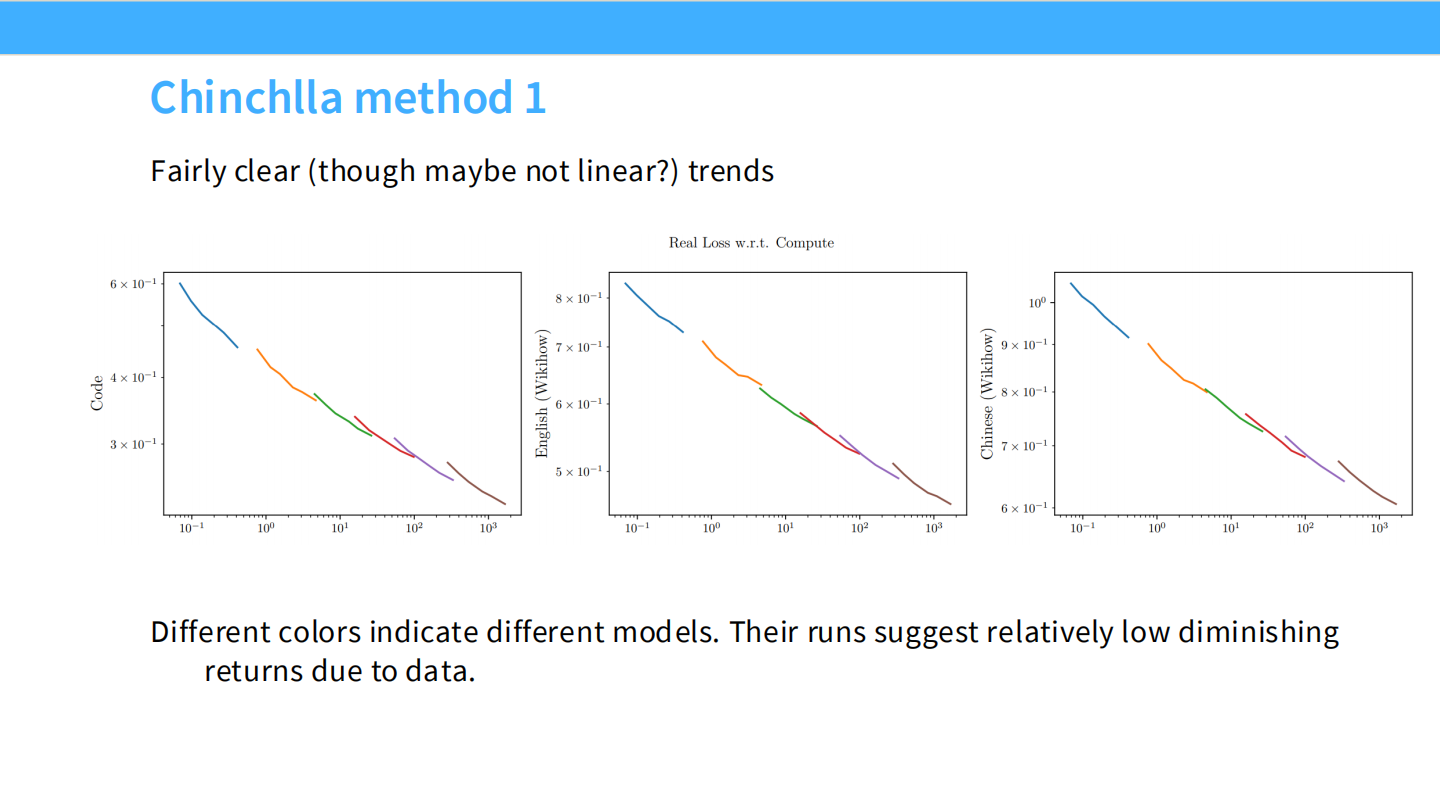
Page 30: Chinchilla 方法 1 (IsoFLOP Curves)

• 图表: 3 个典型的 IsoFLOP 曲线图。
  • 每条抛物线代表一个固定的计算预算（FLOPs）。
  • 最低点: 代表在该预算下的最优模型大小。连接所有最低点，就得到了 Scaling Law。

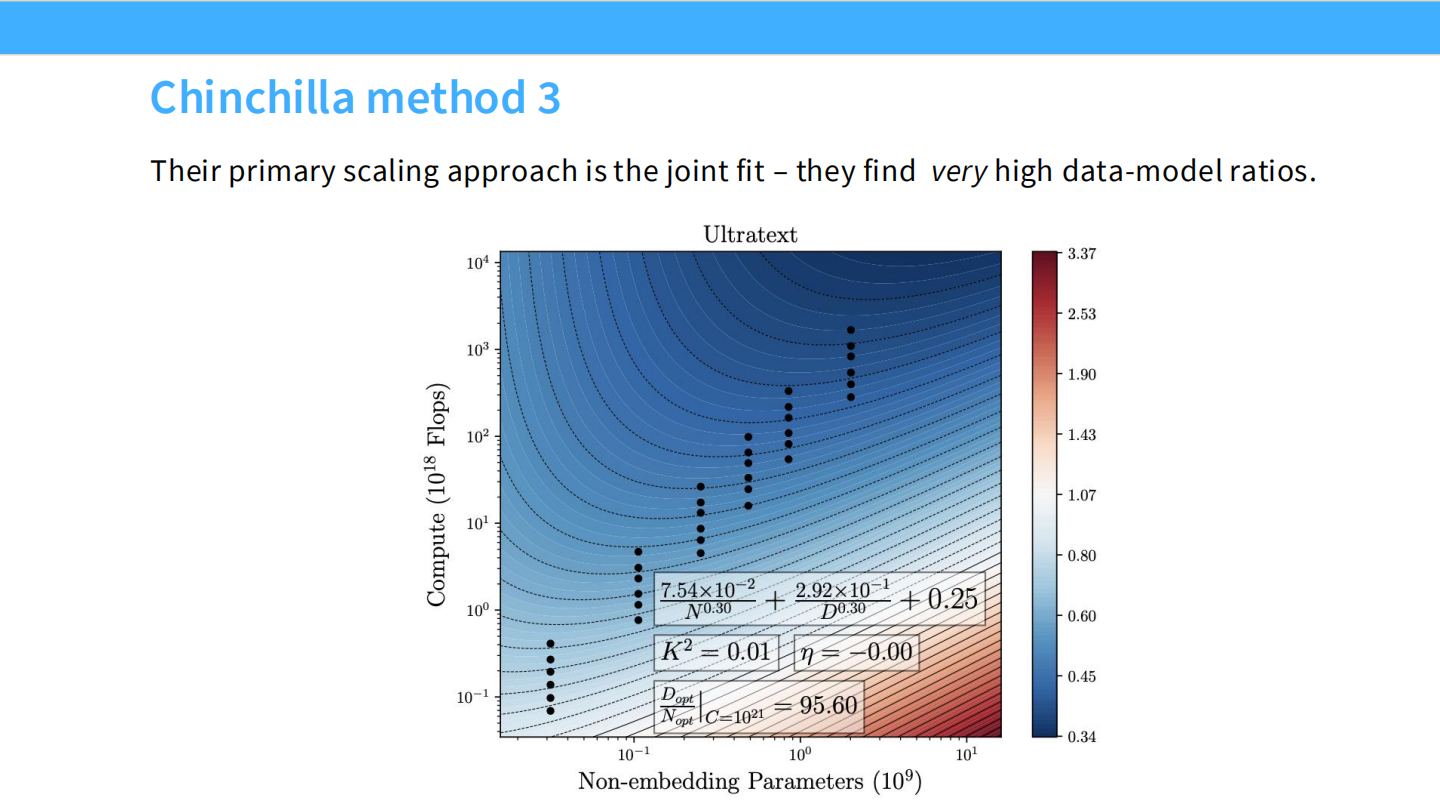
Page 31: Chinchilla 方法 3 (Joint Fit)

• 内容: 直接拟合参数化公式：$L(N, D) = E + AN^{-\alpha} + BD^{-\beta}$。
• 图表: 热力图展示了 Loss 随模型大小 (N) 和数据量 (D) 的变化。

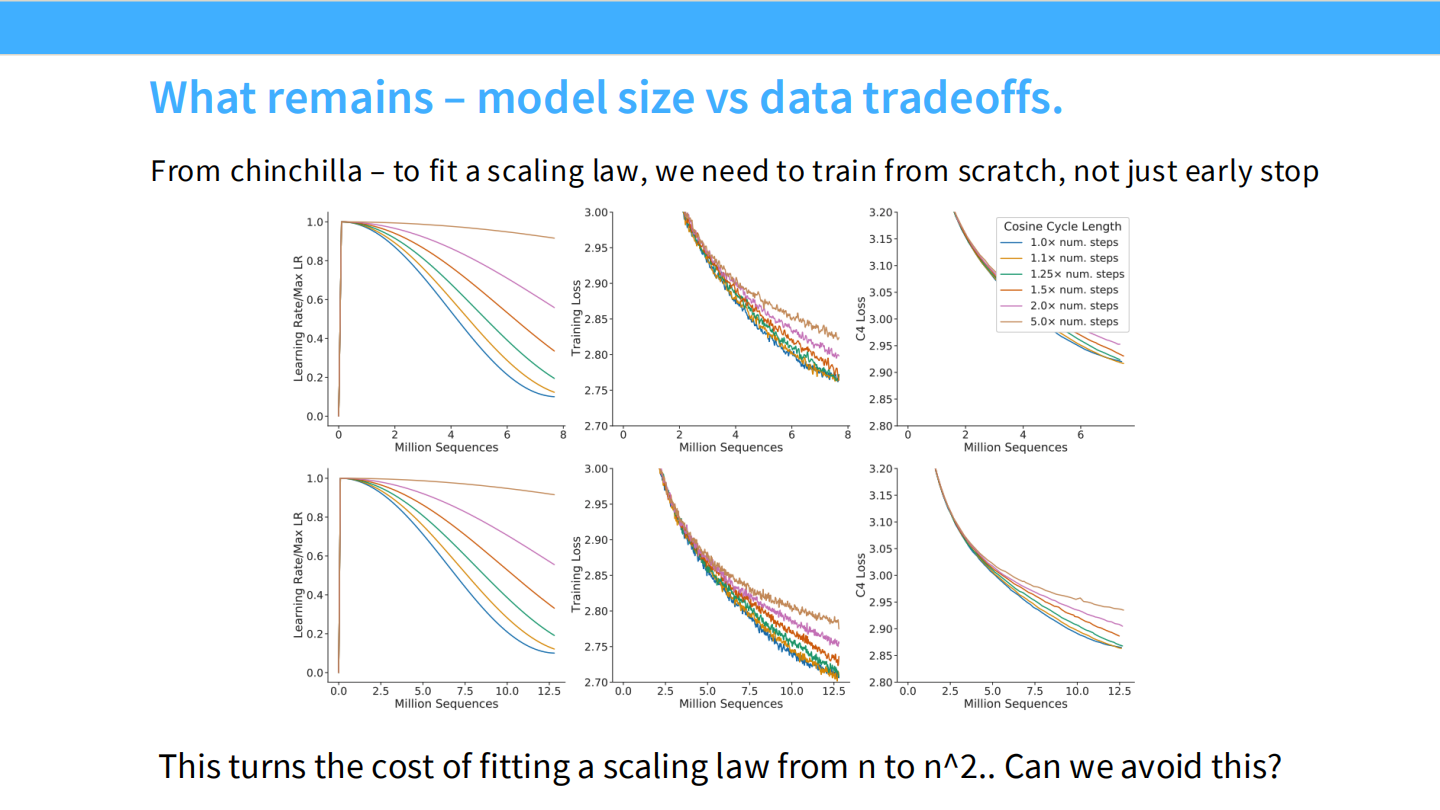
Page 32: 小模型，大数据 (Tiny models with lots of data)

• 现象: 现在的模型（如 Llama 3）数据量远超 Chinchilla 建议（20倍）。Llama 3 达到了 192 倍甚至更多。
• 原因: 虽然训练成本高了，但推理成本低了。为了极致的推理体验（Inference Optimal），我们愿意 Over-train。

---

Part 5: 更多案例 (DeepSeek, Llama 3, etc.)

Page 33: DeepSeek 的 Scaling 分析

• 图表: DeepSeek 在 7B 和 67B 模型发布时，也做了详尽的 Scaling 分析。验证了在小规模模型上拟合的规律可以准确预测大模型。

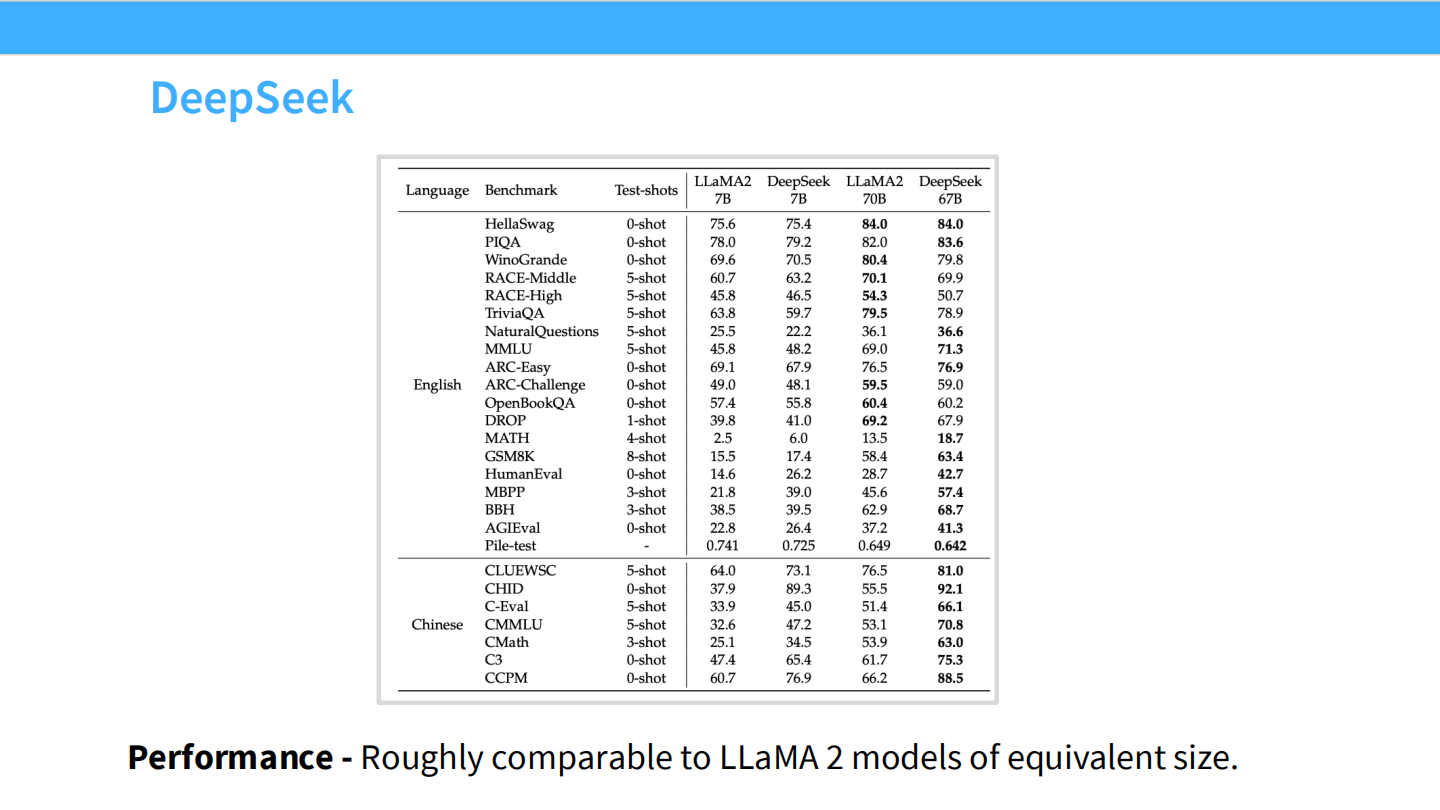
Page 34: DeepSeek 的性能验证

• 表格: DeepSeek 7B/67B 的跑分。性能与同级别的 Llama 2 相当或更好。

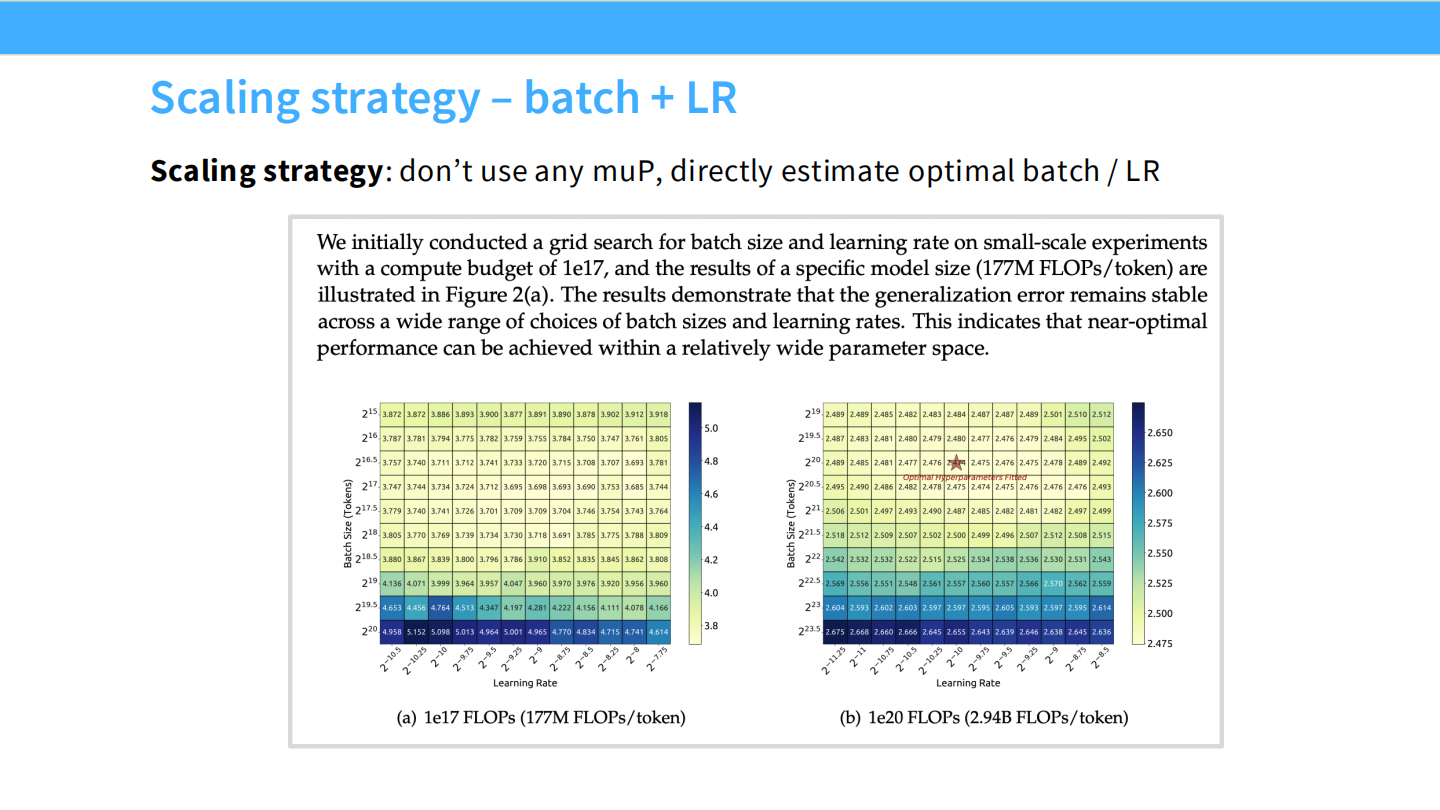
Page 35: 策略 - Batch Size + LR

• 内容: DeepSeek 采用了更传统的网格搜索策略来找最优 LR 和 Batch Size，而不是用 muP。

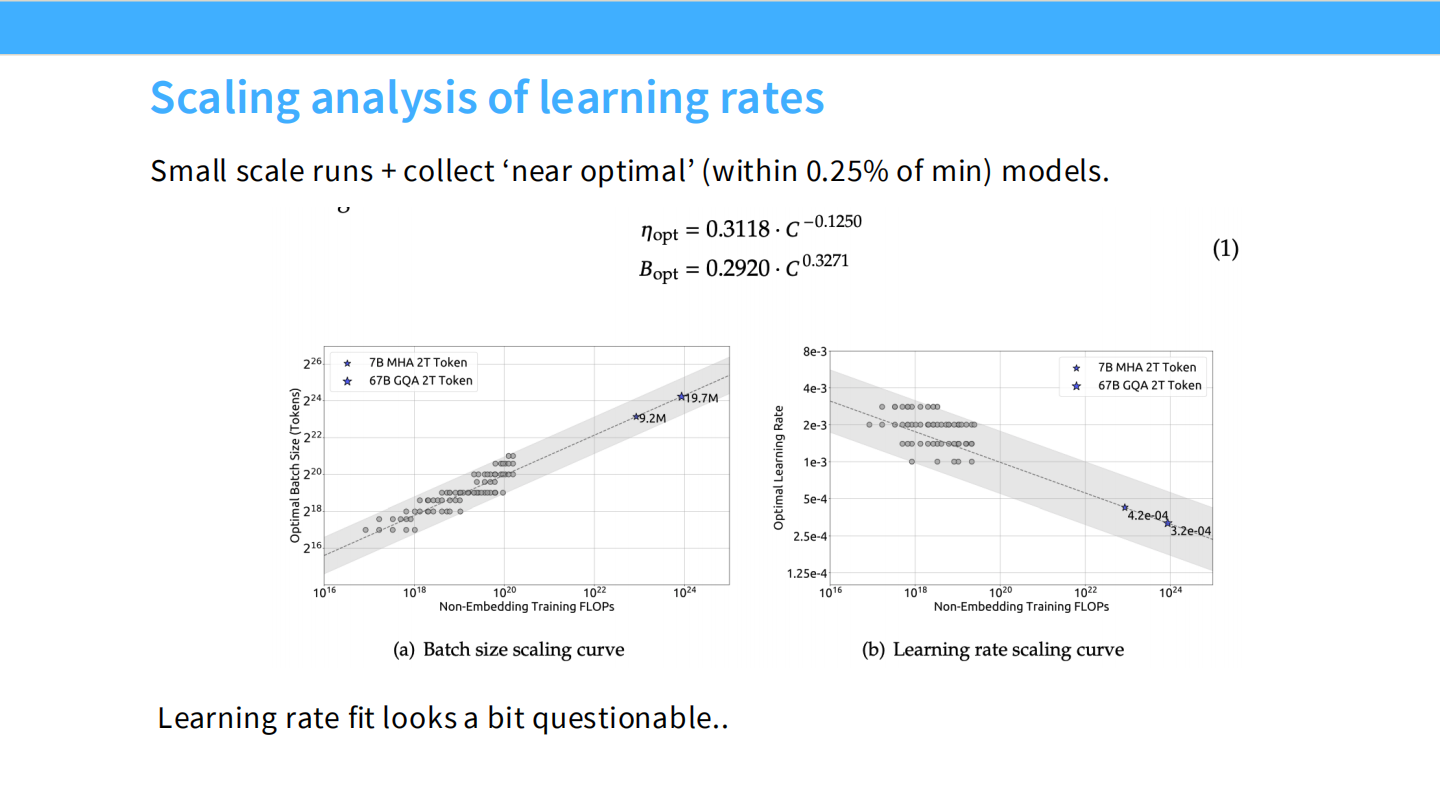
Page 36: 学习率 Scaling

• 图表: 右图展示了 Learning Rate 随 Compute 的变化。最佳 LR 似乎随着计算量增加而减小，但数据点有些噪声。

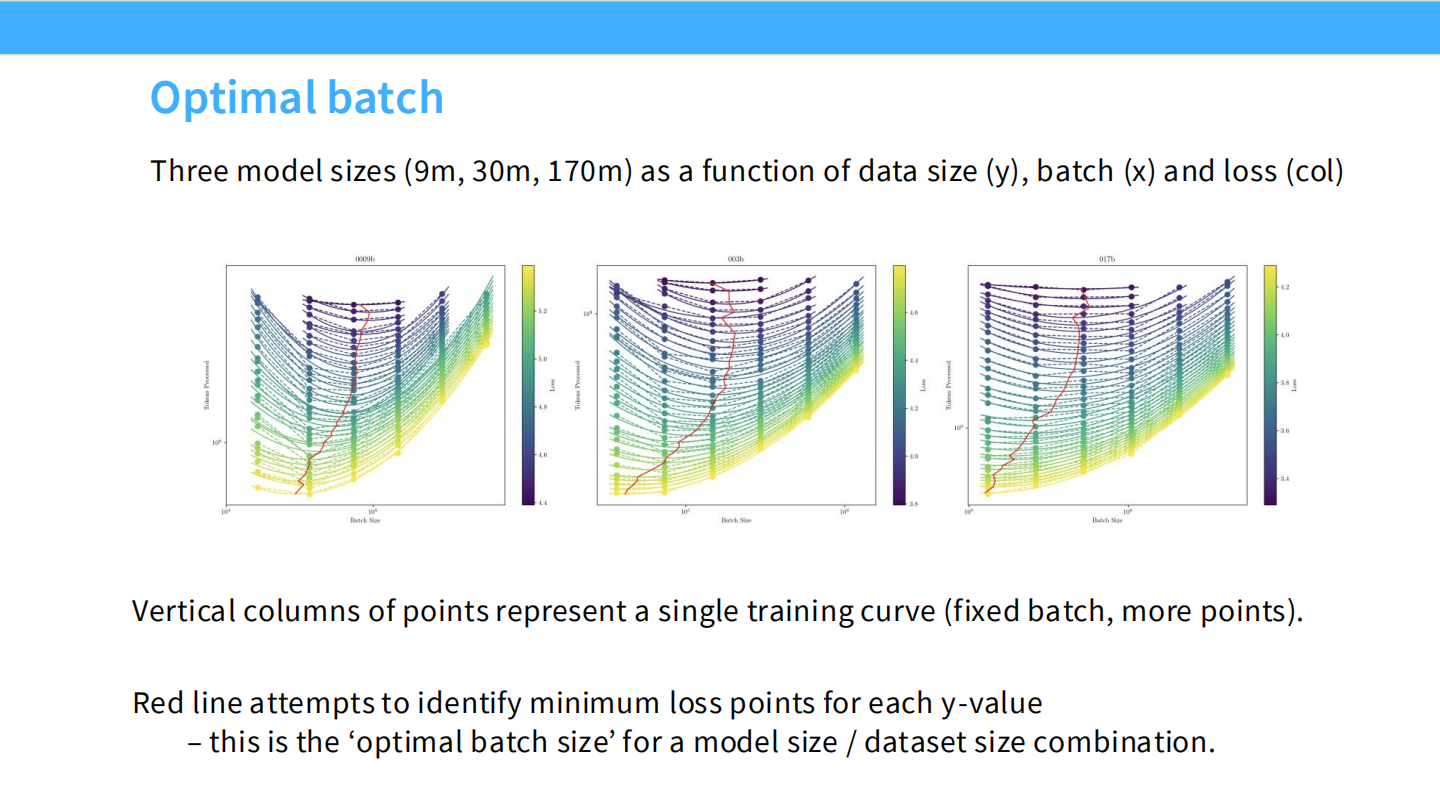
Page 37: 最佳 Batch Size

• 图表: 最佳 Batch Size 随着 Loss 降低（模型变强）而指数级增长。这符合 OpenAI 早期的结论。

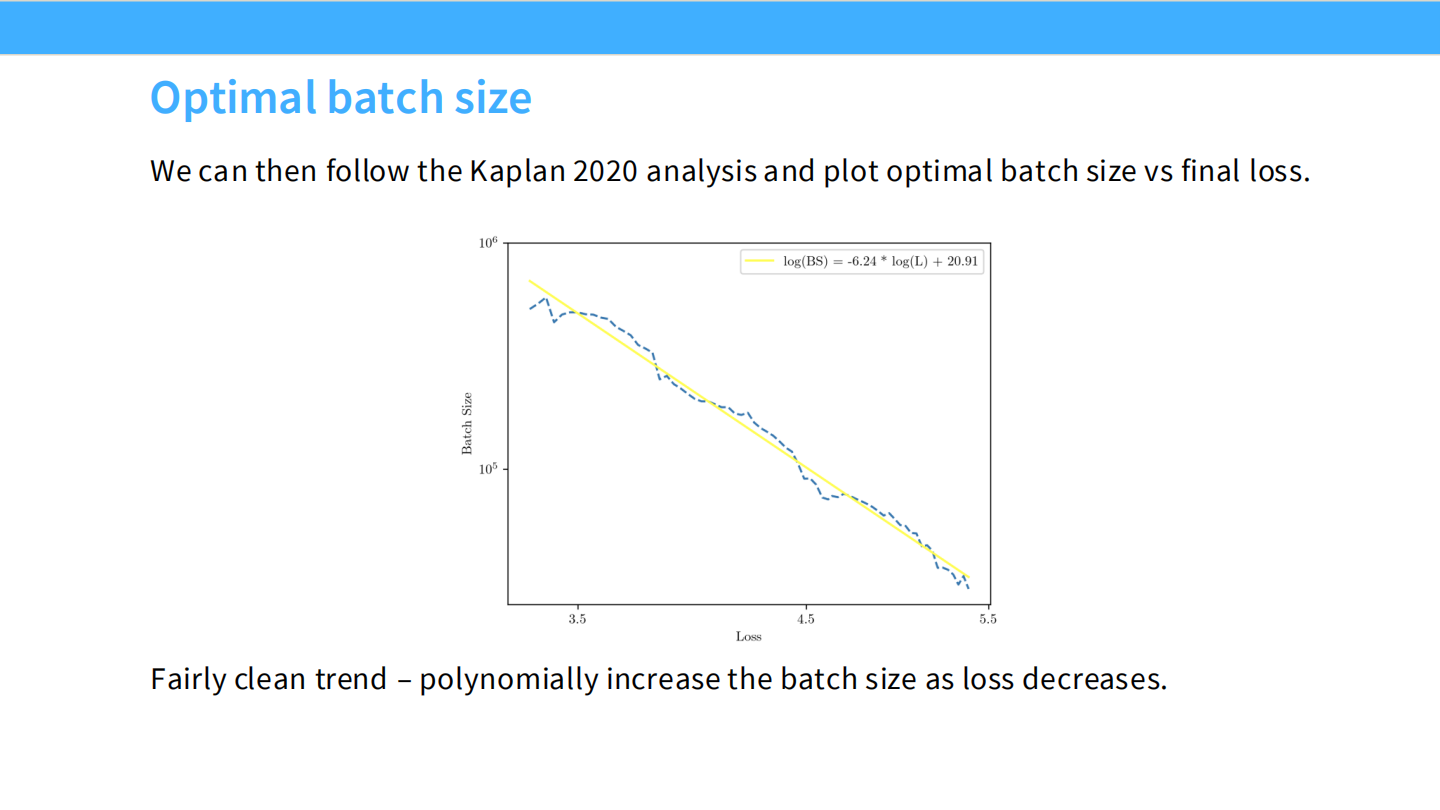
Page 38: 最佳 Batch Size 曲线

• 图表: 将 Batch Size 与 Loss 进行拟合，得到一条干净的多项式曲线。

Page 39: 最佳 LR 稳定性

• 图表: 使用 muP 后，LR 随模型宽度变化的曲线变得平坦（Stable）。这再次验证了 muP 的作用。

Page 40: WSD 调度的细节

• 图表: 展示了 WSD 在不同模型上的 Loss 下降曲线。即使在训练很早期就开始 Decay，也能获得不错的收敛效果。

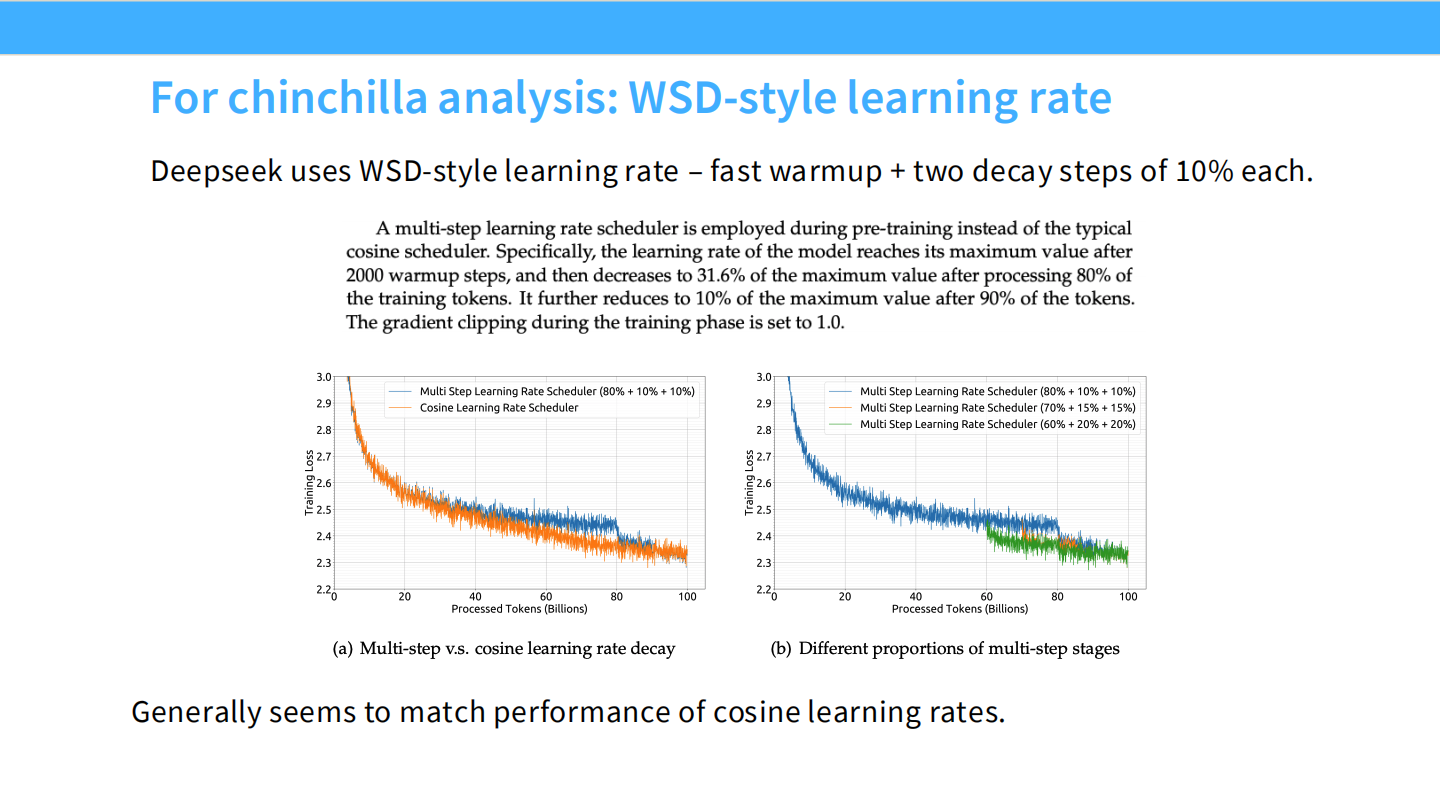
Page 41: 混合 WSD 策略

• 内容: DeepSeek 使用了 WSD 变体：快速 Warmup，然后保持 Stable，最后分阶段 Decay (80% + 10% + 10%)。

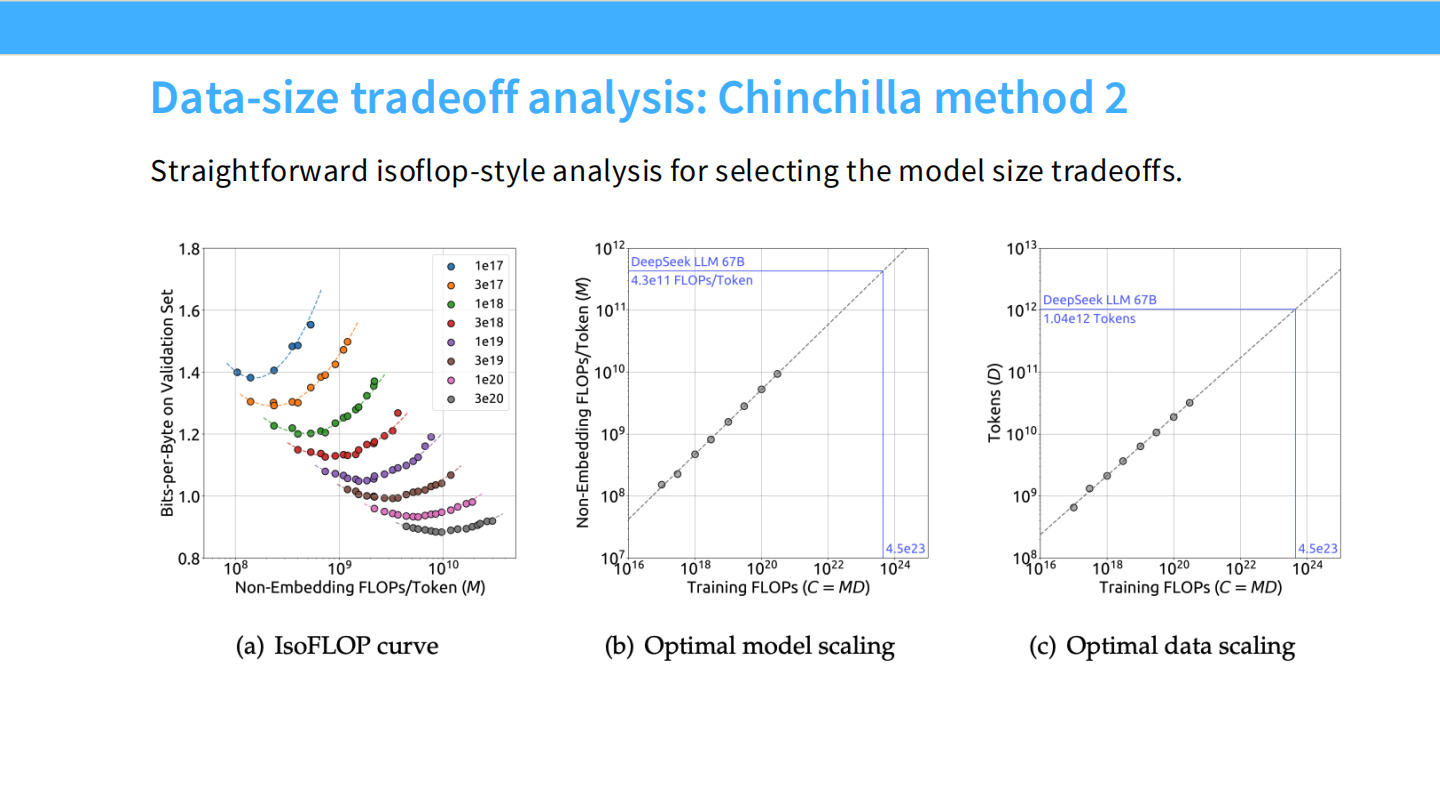
Page 42: IsoFLOP 分析 (DeepSeek)

• 图表: DeepSeek 复现了 Chinchilla 的 IsoFLOP 曲线（左图）和最优模型/数据扩展曲线（中/右图）。

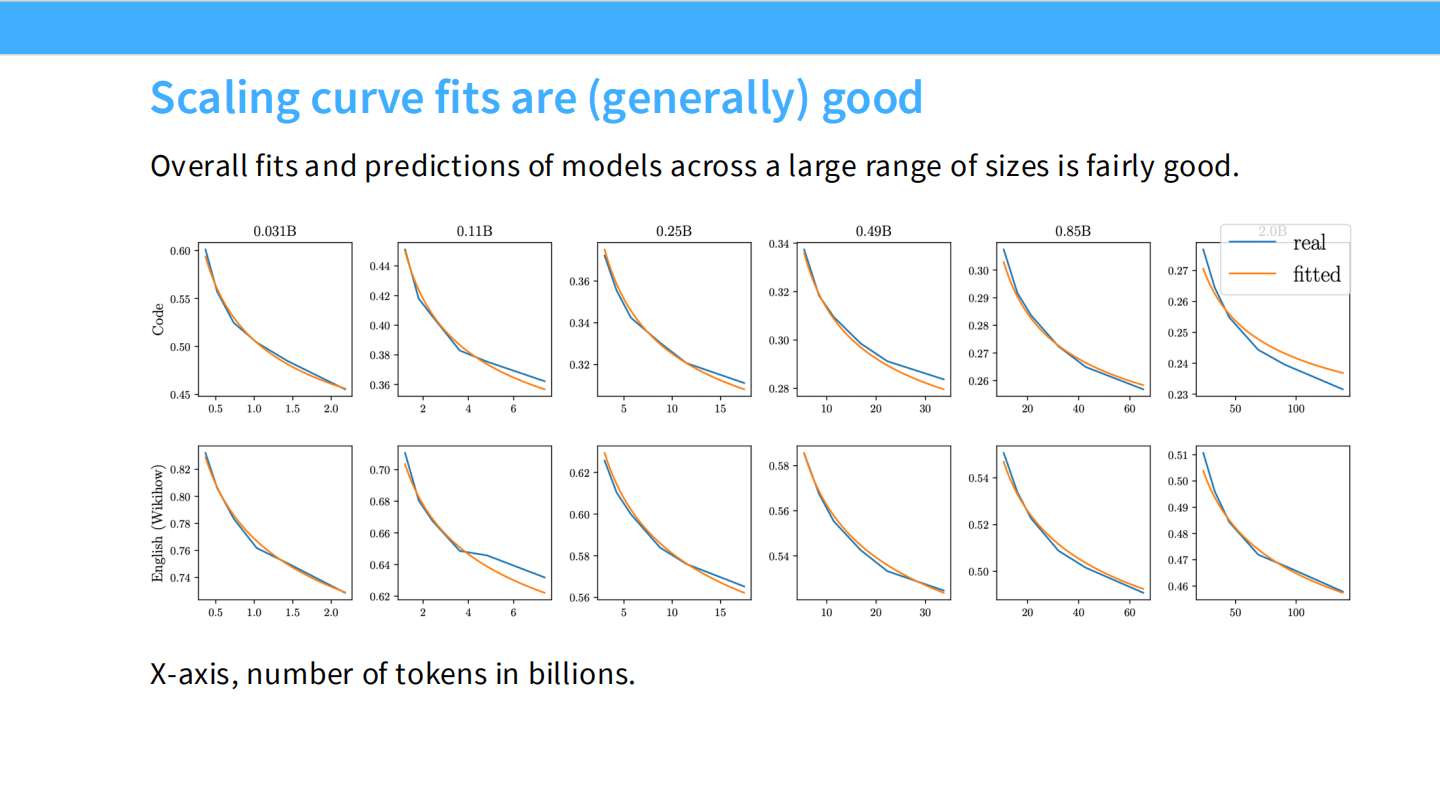
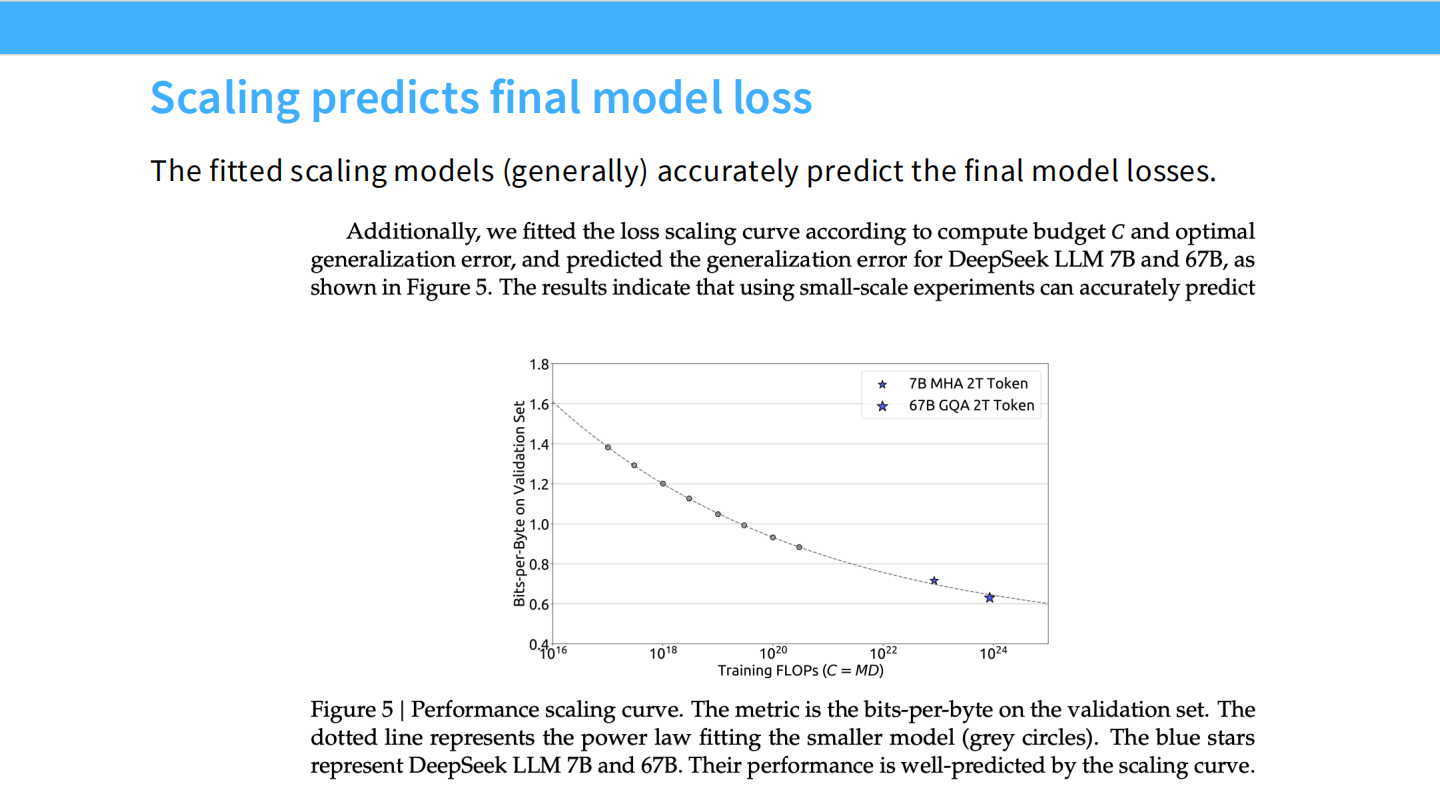
Page 43: 预测最终 Loss

• 图表: 预测值与实际值的对比。Scaling Law 的预测精度非常高。

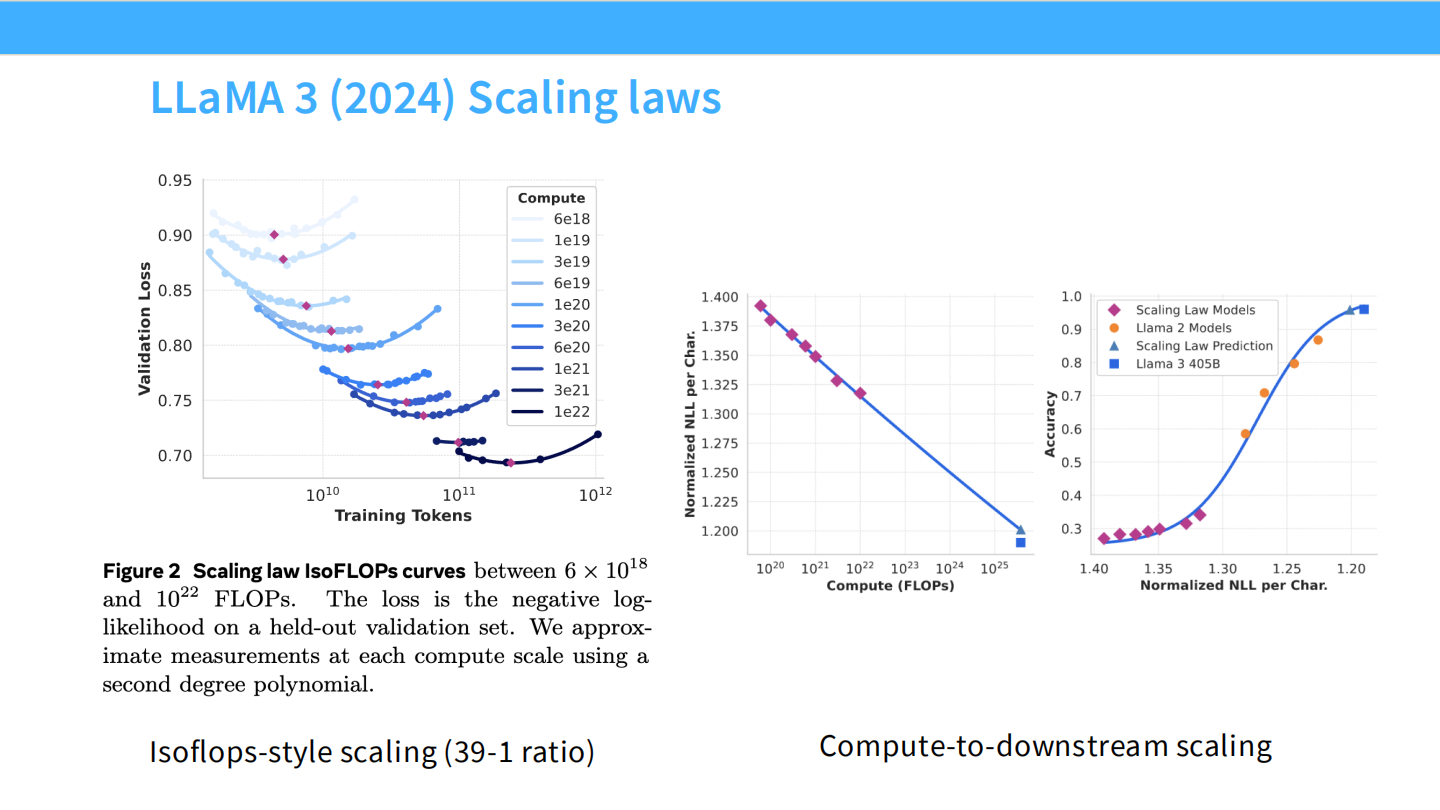
Page 44: Llama 3 的 Scaling

• 图表: Llama 3 的 IsoFLOPs 曲线。
• 关键点: 即使在 $10^{25}$ FLOPs 这样巨大的计算量下，Scaling Law 依然成立，没有饱和。

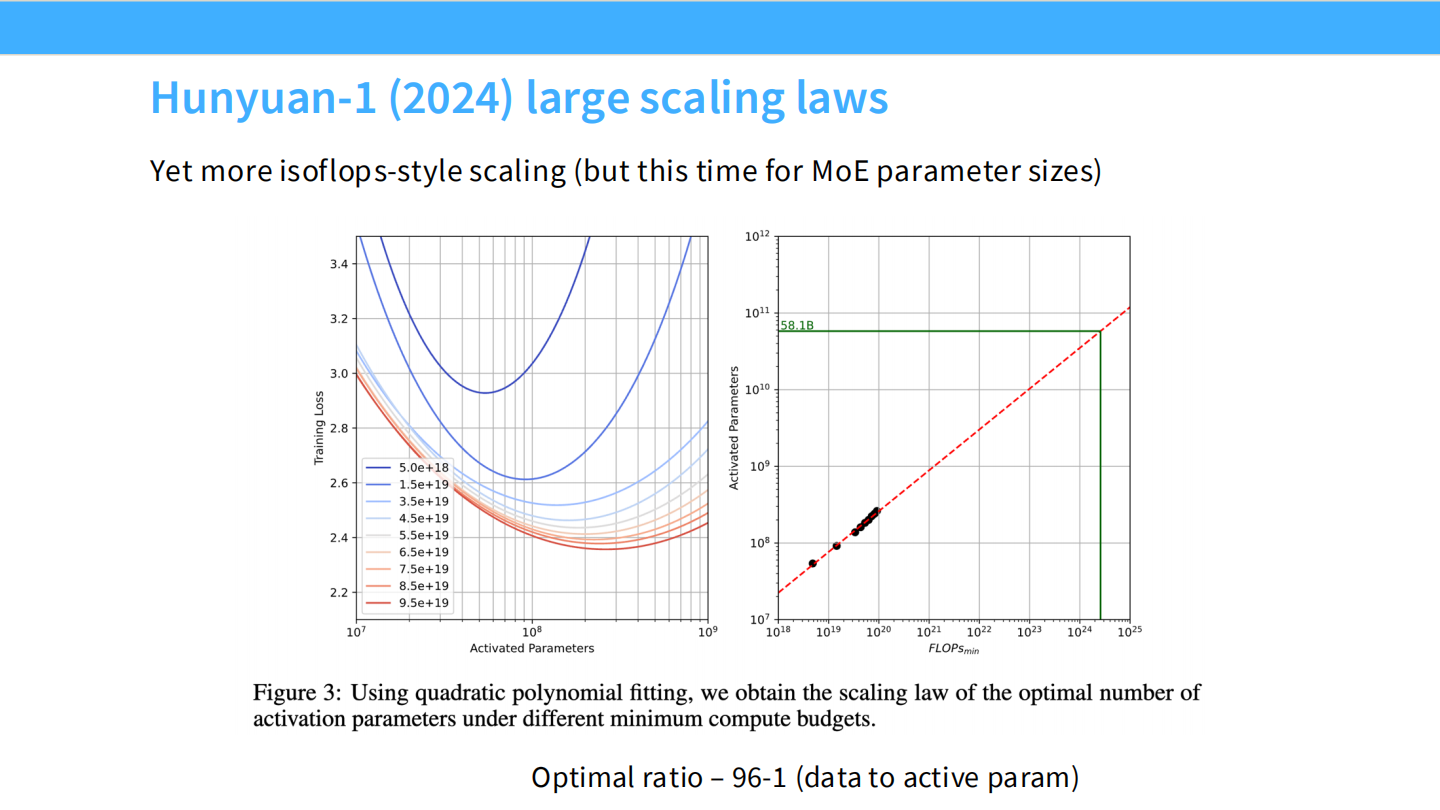
Page 45: 腾讯混元 (Hunyuan-Large)

• 图表: 混元 MoE 模型的 Scaling 曲线。
• 结论: MoE 同样遵循 Scaling Law，且能用更少的计算量达到同样的 Loss。

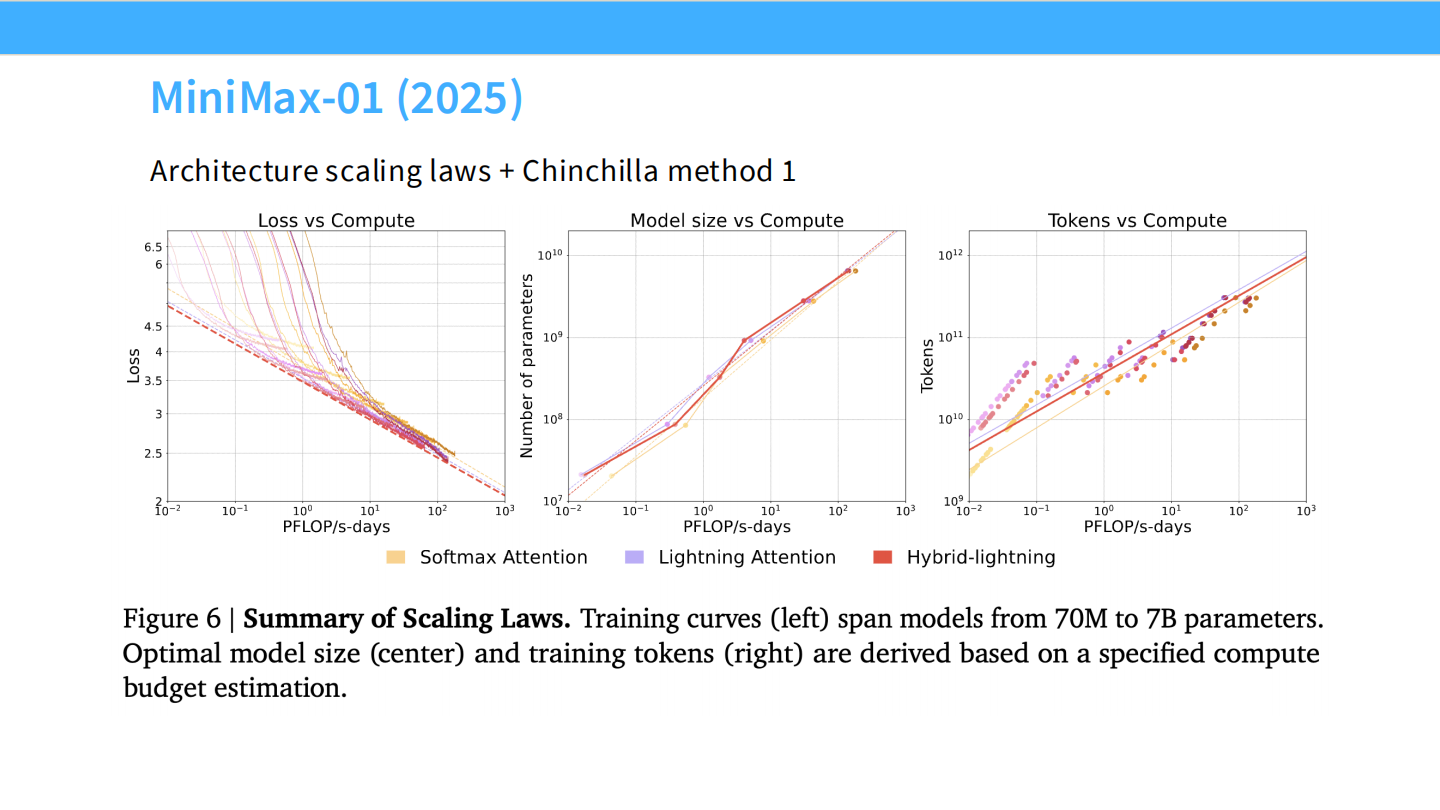
Page 46: MiniMax-01

• 图表: Loss vs Compute。
• 亮点: MiniMax 采用了 Lightning Attention（线性 Attention）。这表明非 Transformer 架构也遵循类似的 Scaling 规律。

Page 47: Scaling Recipe 总结 (Part 1)

• Cerebras-GPT: 使用 muP + Chinchilla 公式。
• DeepSeek: 假设超参数不变 + 小规模网格搜索 + IsoFLOP 分析。

Page 48: Scaling Recipe 总结 (Part 2)

• MiniCPM: muP + WSD 调度 + Chinchilla 联合拟合。
• Llama 3: 纯粹的 IsoFLOPs（暴力美学）。
• MiniMax: 架构选择（线性 Attention）的 Scaling。

Page 49: muP 验证

• 图表: 再次展示了 muP 如何让 LR 调优变得 Scale-invariant。

Page 50: muP 的定义回顾

• 内容: 引用 muP 原论文的定义。A1 (Init) 和 A2 (Update) 条件。

Page 51: A1 条件推导

• 数学: 矩阵乘法的范数性质。$|W h| \approx \sqrt{n}$。

Page 52: A2 条件推导

• 数学: 梯度更新对输出的影响。

Page 53: A2 条件推导 (Part 2)

• 数学: 最终得出 LR $\eta = \Theta(1/n)$ 的结论。

Page 54: muP Recap

• 总结: muP 的核心就是控制 Activations 和 Updates 的规模。

Page 55: 全课回顾 (Recap for the whole lecture)

• 挑战: 扩展模型面临架构参数、优化器参数和计算成本的挑战。
• 解法:
  1. 稳定性: 假设稳定性或使用 muP。
  2. 搜索: 在小规模上搜 LR/Batch，然后预测。
  3. 调度: 使用 WSD 调度来低成本拟合曲线。