大模型从0到1｜第五讲：详解 GPU 架构与性能优化

讲师： Tatsu H
核心主题： 深入剖析 GPU 的底层硬件原理、性能分析方法论（Roofline Model），以及如何通过 Tiling、Fusion、Coalescing 等技巧优化深度学习负载，最后以 FlashAttention 为例进行融会贯通。

---

Part 1: GPU 深度解析 (GPUs in Depth)

Page 1: 课程标题

• 内容解析： 课程正式开始。本节课的主题是 GPUs。在深度学习时代，理解 GPU 不仅仅是系统工程师的工作，对于算法工程师理解模型扩展性（Scaling）和性能瓶颈至关重要。

Page 2: 课程大纲

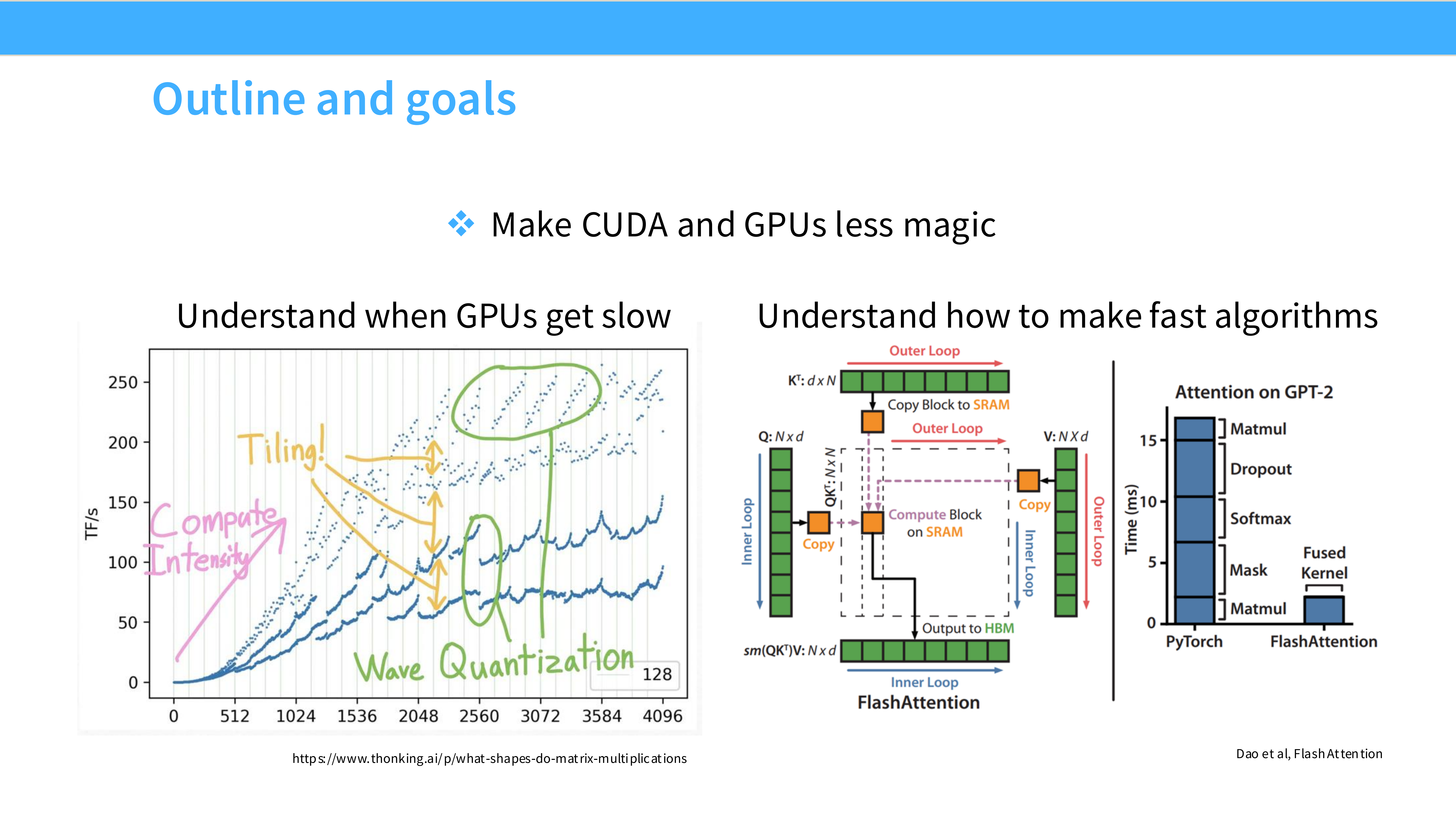
• 内容解析： 本节课的组织结构分为三部分：
  1. Part 1: GPUs in depth —— 深入硬件底层，讲解 GPU 的工作原理、内存层级和核心组件。
  2. Part 2: Understanding GPU performance —— 讲解如何让 GPU 跑得快，介绍 Roofline 模型和关键优化技巧。
  3. Part 3: Putting it together —— 拆解 FlashAttention，看它如何综合运用上述技巧解决实际问题。

Page 3: 致谢与资源

• 内容解析： 课程内容参考了多个高质量来源。
  • Horace He’s blog: “Thonk From First Principles”，非常硬核的 ML 系统博客。
  • CUDA MODE: 一个专注于 CUDA 编程和高性能计算的开源社区和 Discord 群组，推荐学生加入。

Page 4: 背景 - 算力即性能

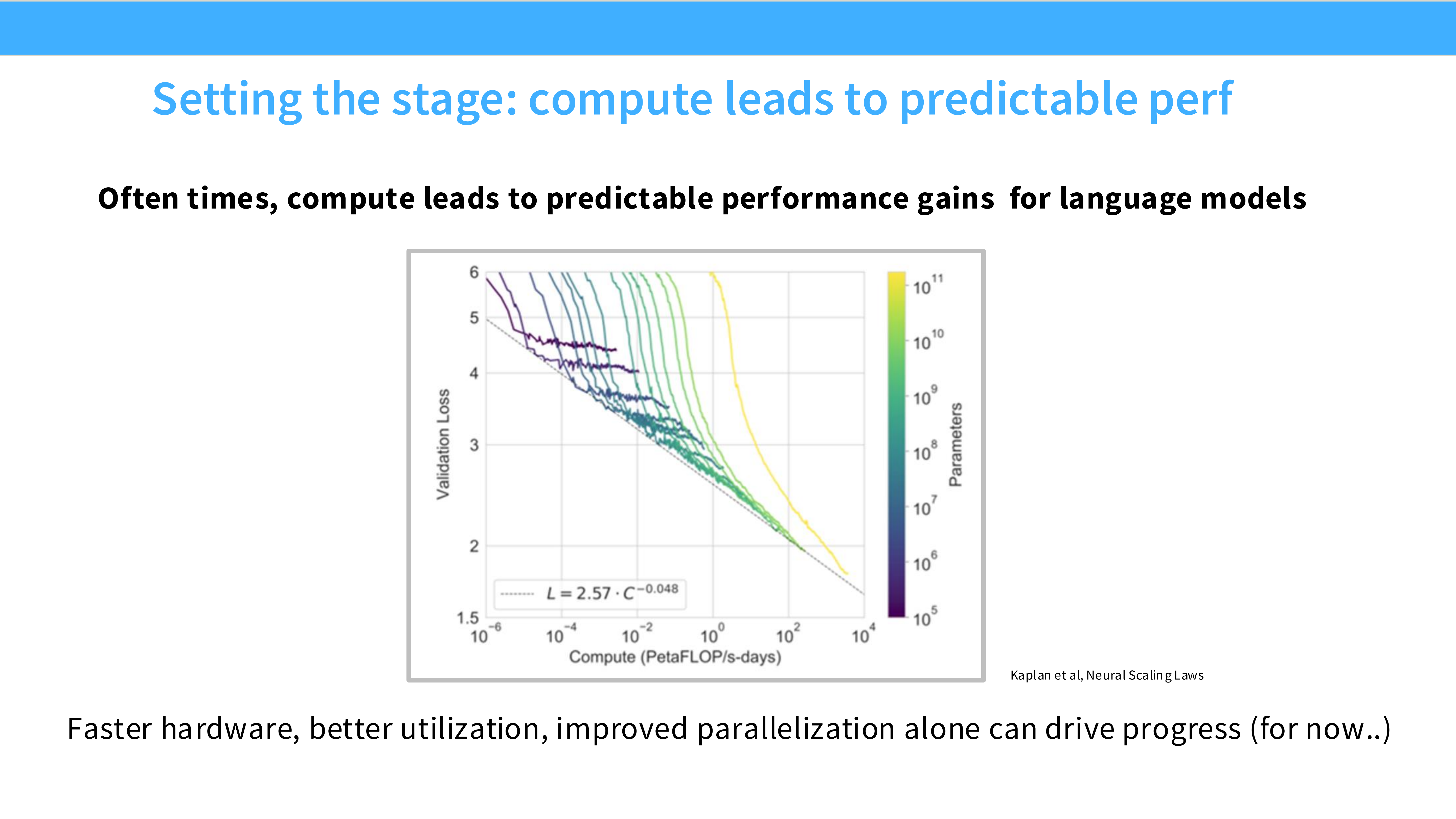
• 内容解析： 这张图展示了 Scaling Laws（扩展定律）。
  • 现象： 随着计算量（Compute, PetaFLOP/s-days）的指数级增加，模型的 Loss 呈现线性下降趋势。
  • 结论： 对于语言模型来说，算力通常能直接转化为可预测的性能提升。硬件越快，我们在单位时间内能跑的算力越多，模型效果就越好。

Page 5: 计算扩展的瓶颈 - Dennard Scaling 失效

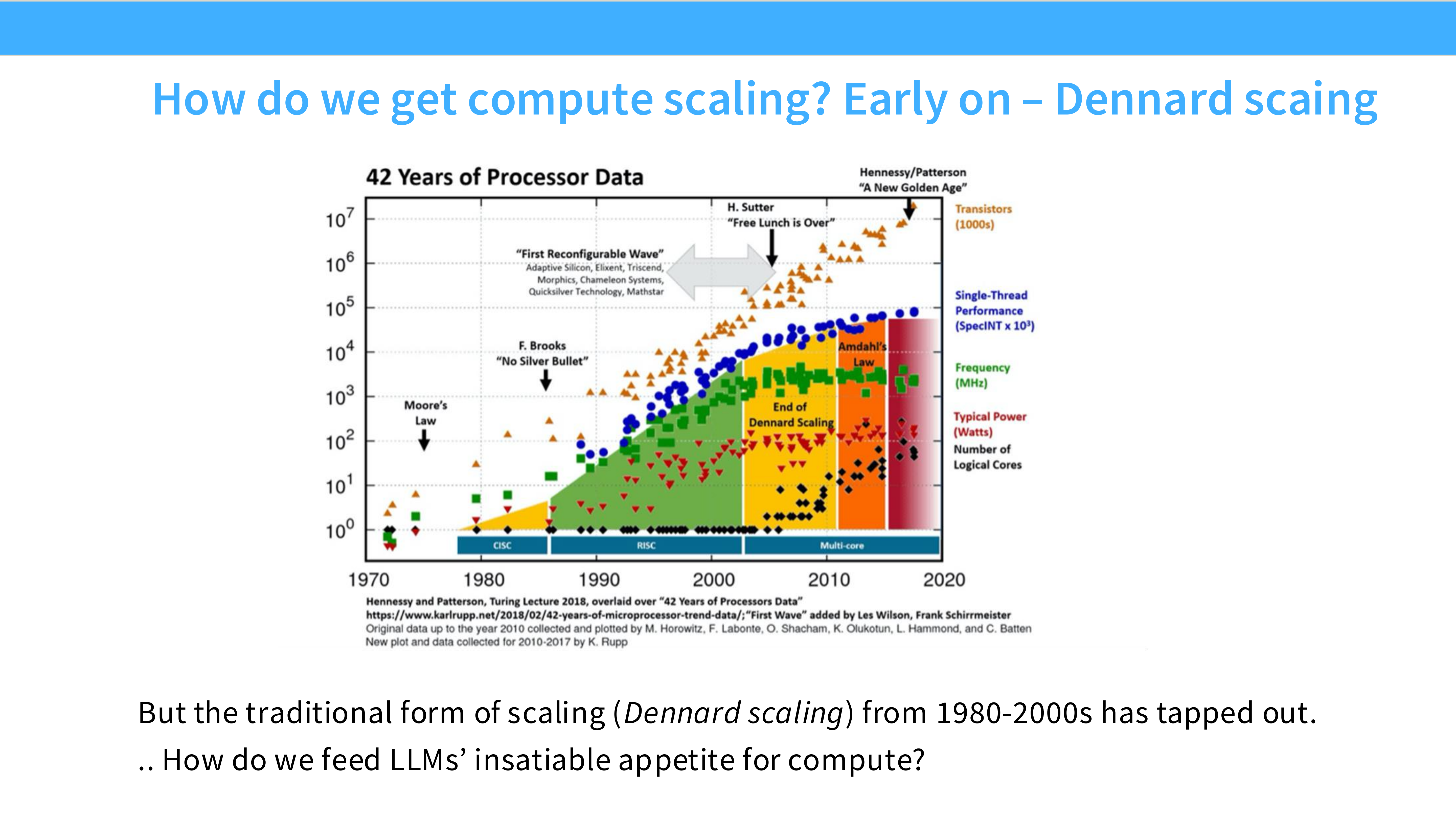
• 内容解析： 回顾处理器历史（1970-2010）。
  • 趋势： 绿色点代表频率（Frequency）。在 2005 年之前，频率随时间指数增长；但 2005 年后，频率增长停滞（Plateau）。
  • 原因： Dennard Scaling（登纳德缩放比例定律） 失效。由于功耗和散热限制（Power Wall），单核性能无法再通过单纯提高主频来提升。这迫使我们寻找新的扩展路径。

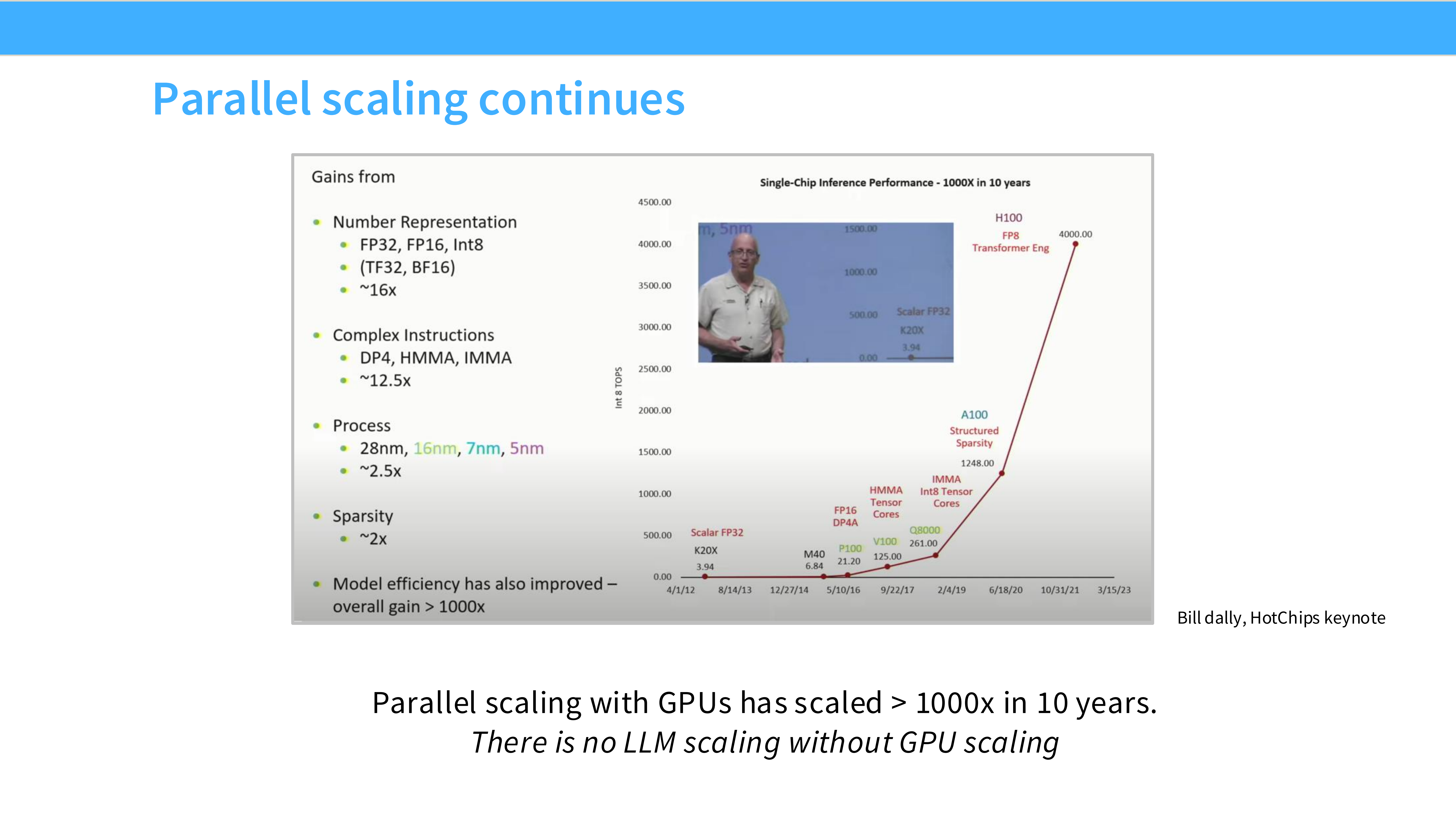
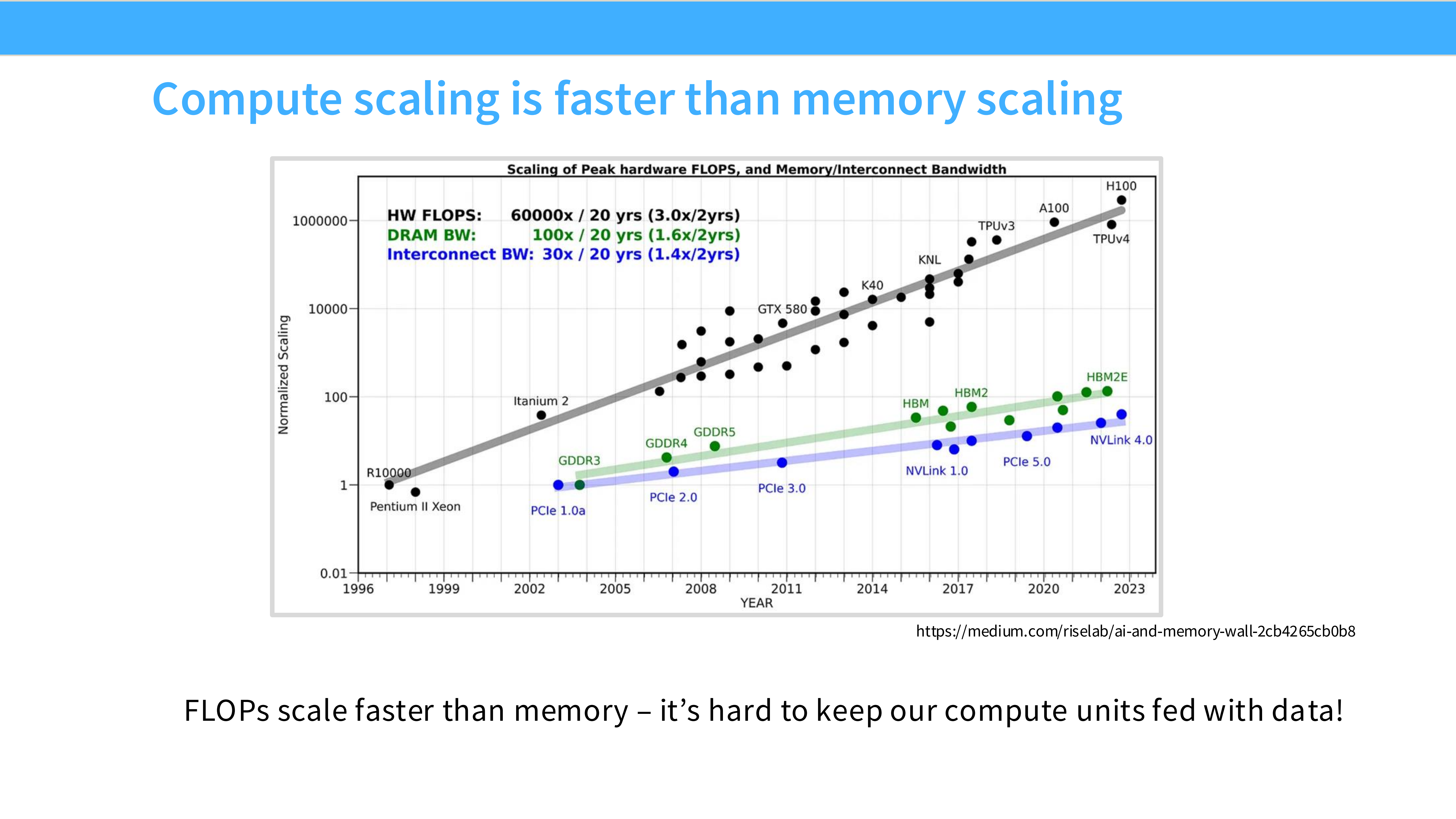
Page 6: 并行扩展的接力 (Parallel Scaling)

• 内容解析： 既然单核快不起来，那就堆核心。
  • 图表： 展示了 GPU（如 K80 到 H100）和 TPU 算力在过去 10 年的爆发式增长。
  • 关键点： 虽然内存带宽（Memory）也在增长，但计算能力（Compute, 尤其是低精度计算）的增长速度远超内存。
  • 结论： LLM 的扩展完全依赖于 GPU 的并行扩展能力。

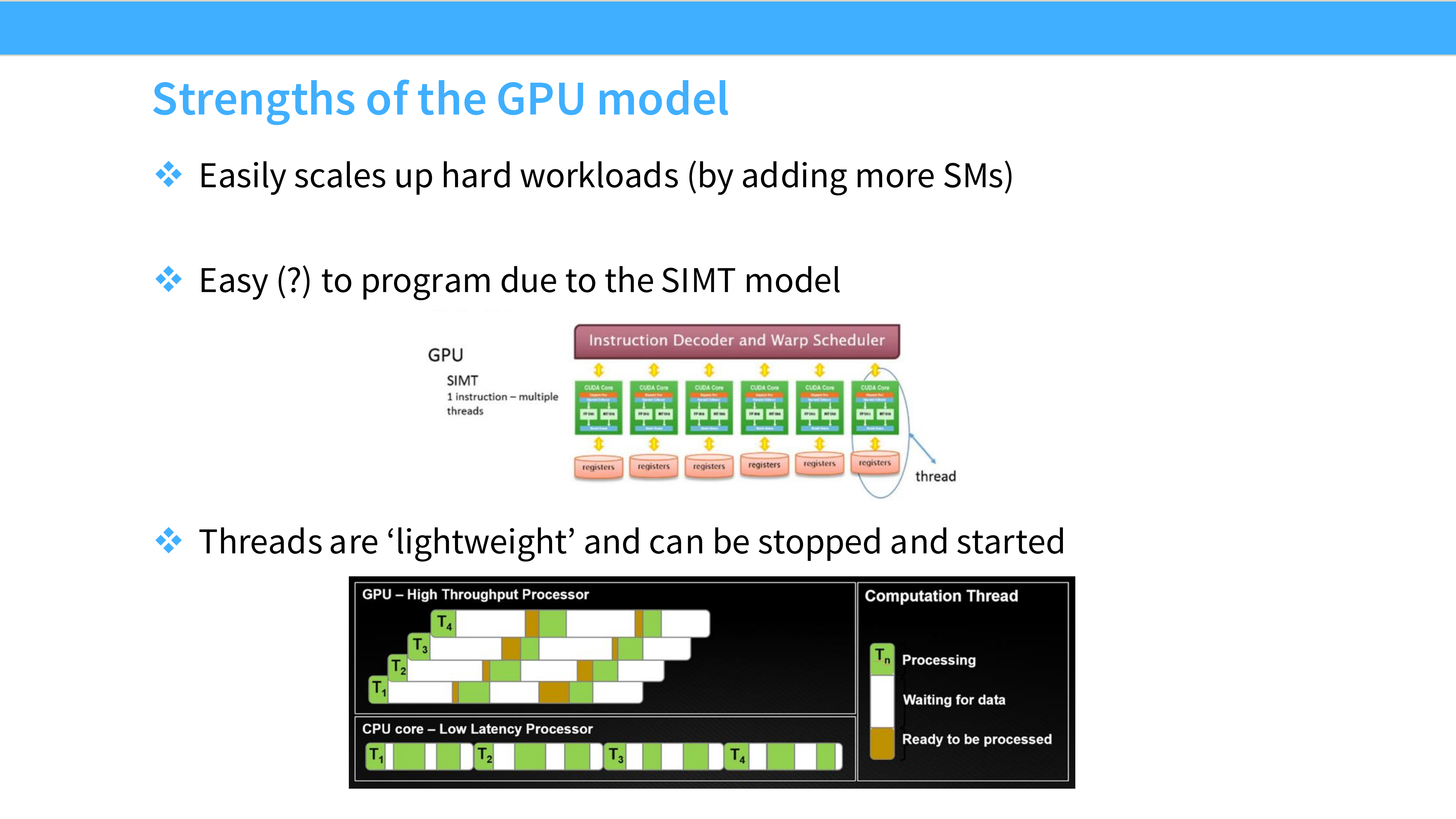
Page 7: GPU 模型的优势

• 内容解析： 为什么 GPU 能成为 AI 的主力？
  1. 易于扩展 (Scalability)： GPU 架构是模块化的，可以通过增加 SM (Streaming Multiprocessors) 轻松扩展算力。
  2. 编程模型 (SIMT)： 单指令多线程。虽然编写复杂，但适合处理大规模数据并行任务。
  3. 轻量级线程： GPU 线程启动和切换极快，能够以低开销隐藏延迟。

Page 8: CPU vs. GPU 架构设计

• 内容解析：
  • CPU (左)： 巨大的 Cache 和复杂的 Control 单元，ALU（计算单元）占比小。
    • 目标： **低延迟 (Latency)**。擅长逻辑复杂的串行任务。
  • GPU (右)： 绝大部分面积是绿色的 ALU，Control 和 Cache 很小。
    • 目标： **高吞吐 (Throughput)**。擅长海量数据的并行处理，不介意单个任务的延迟，只在乎整体完成量。

Page 9: GPU 解剖 - 宏观与微观

• 内容解析：
  • GA100 Full GPU (右)： 宏观上看，GPU 由 128 个 SM (Streaming Multiprocessors) 组成。
  • SM 内部 (左)： 每个 SM 包含多个 SP (Streaming Processor) 也就是 CUDA Core，以及专用的 Tensor Cores（用于矩阵加速）、寄存器堆（Register File）和调度器。

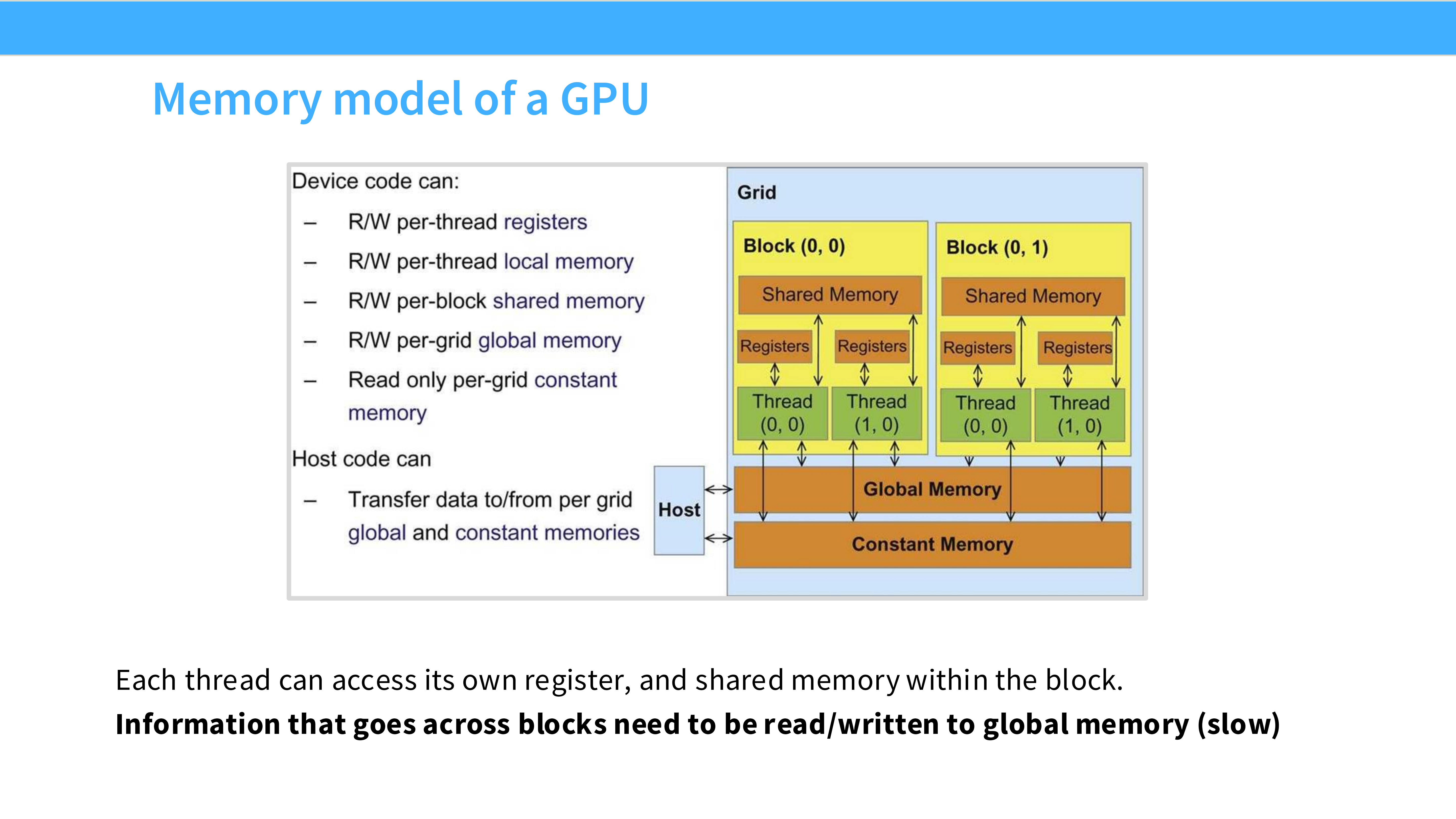
Page 10: GPU 解剖 - 内存层级

• 内容解析： 理解内存位置是优化的关键。
  • L1 Cache / Shared Memory： 位于 SM 内部（图中绿色部分），是 SRAM。速度极快（19 TB/s），但容量极小。
  • L2 Cache： 芯片中间，所有 SM 共享。
  • HBM (High Bandwidth Memory)： 芯片边缘的显存颗粒。这是 DRAM，容量大（40-80GB），但速度最慢（1.5-2.0 TB/s）。
  • 法则： 离计算单元越近，速度越快，容量越小。

Page 11: GPU 执行模型

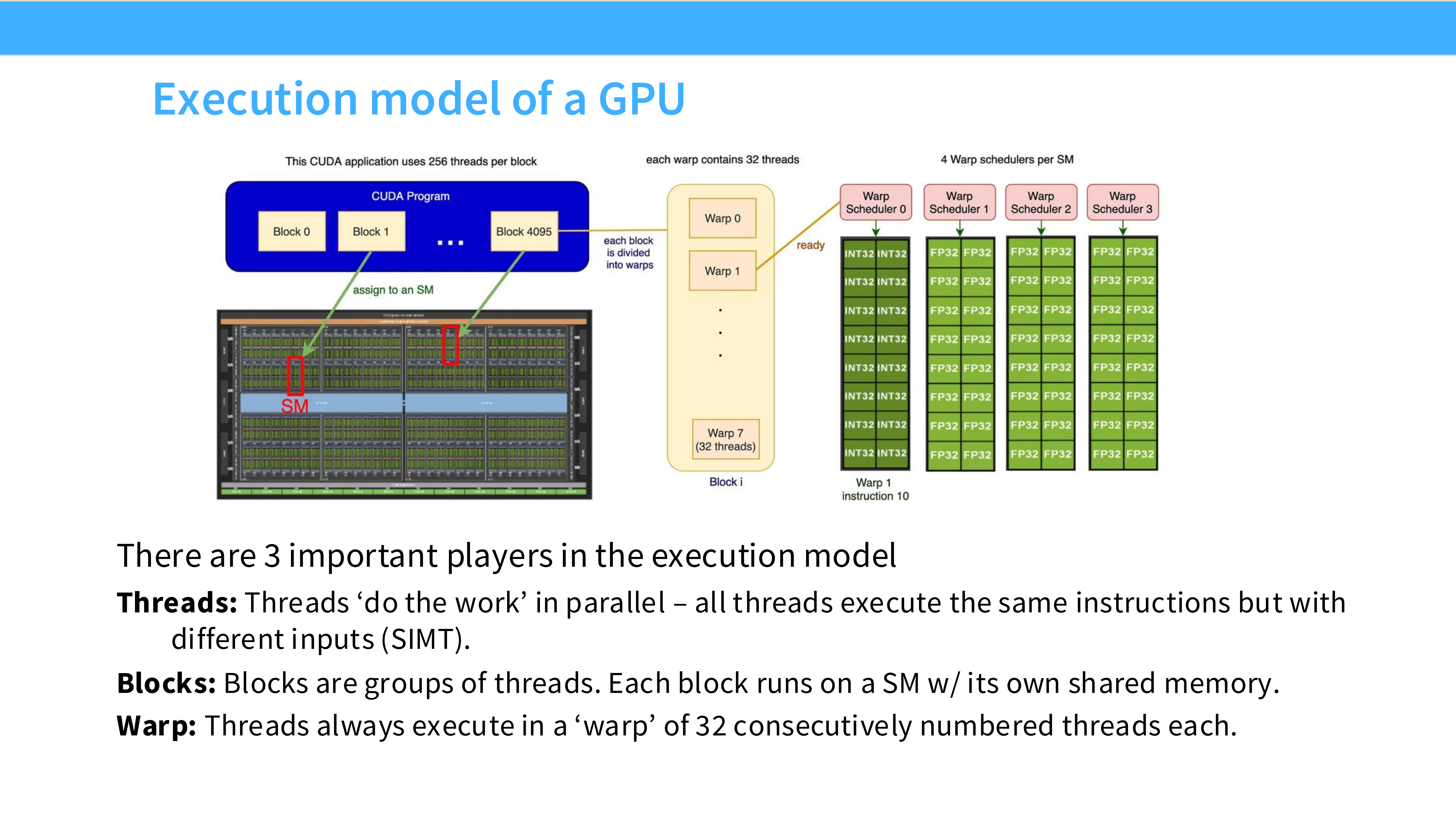
• 内容解析： 软件层面的三个核心概念：
  1. Threads (线程)： 并行工作的最小单位。
  2. Blocks (线程块)： 一组线程，运行在同一个 SM 上，共享该 SM 的 Shared Memory。
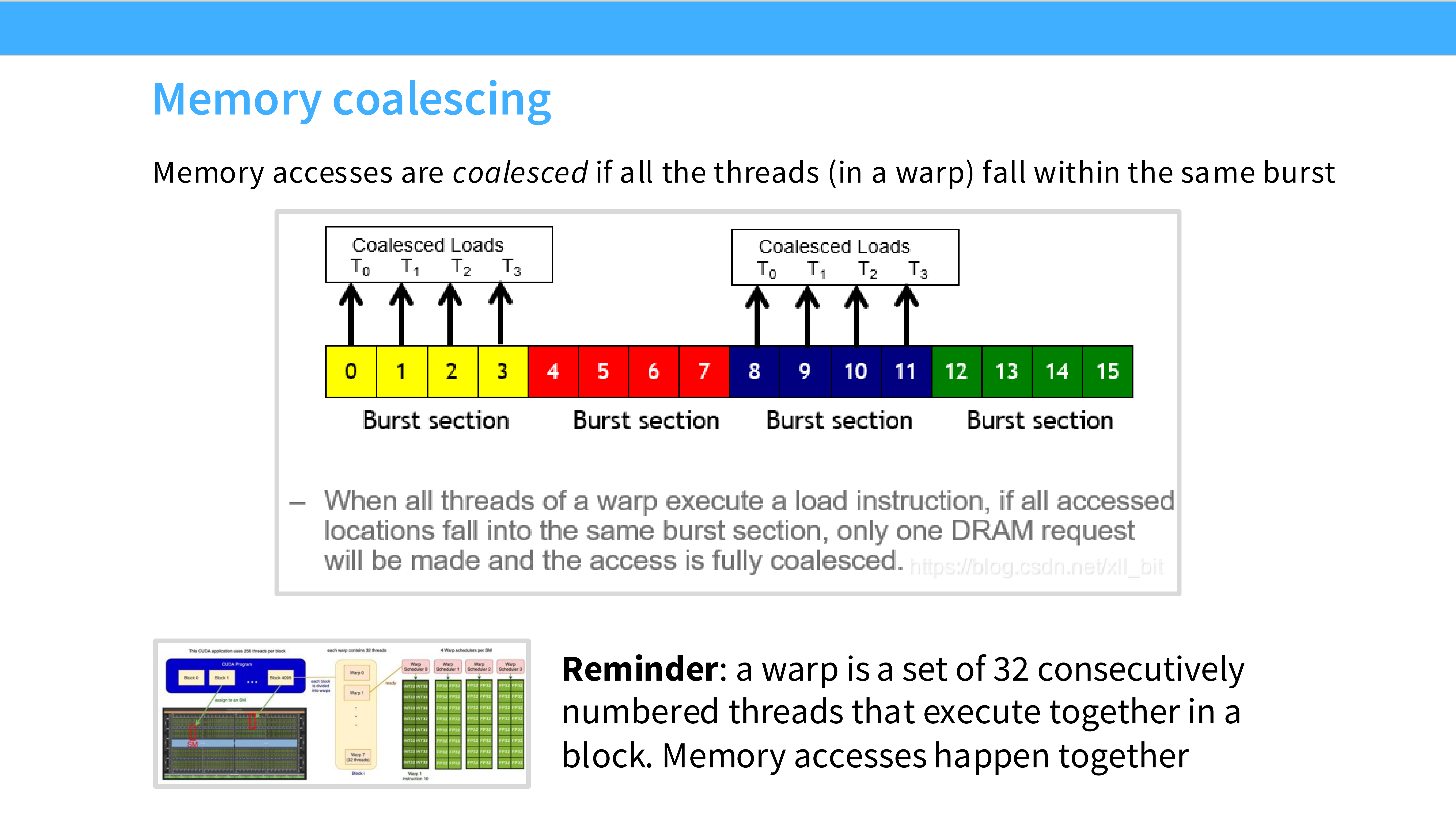
  3. Warps (线程束)： 硬件调度的最小单位，通常由 32 个连续线程 组成，物理上同步执行同一条指令。

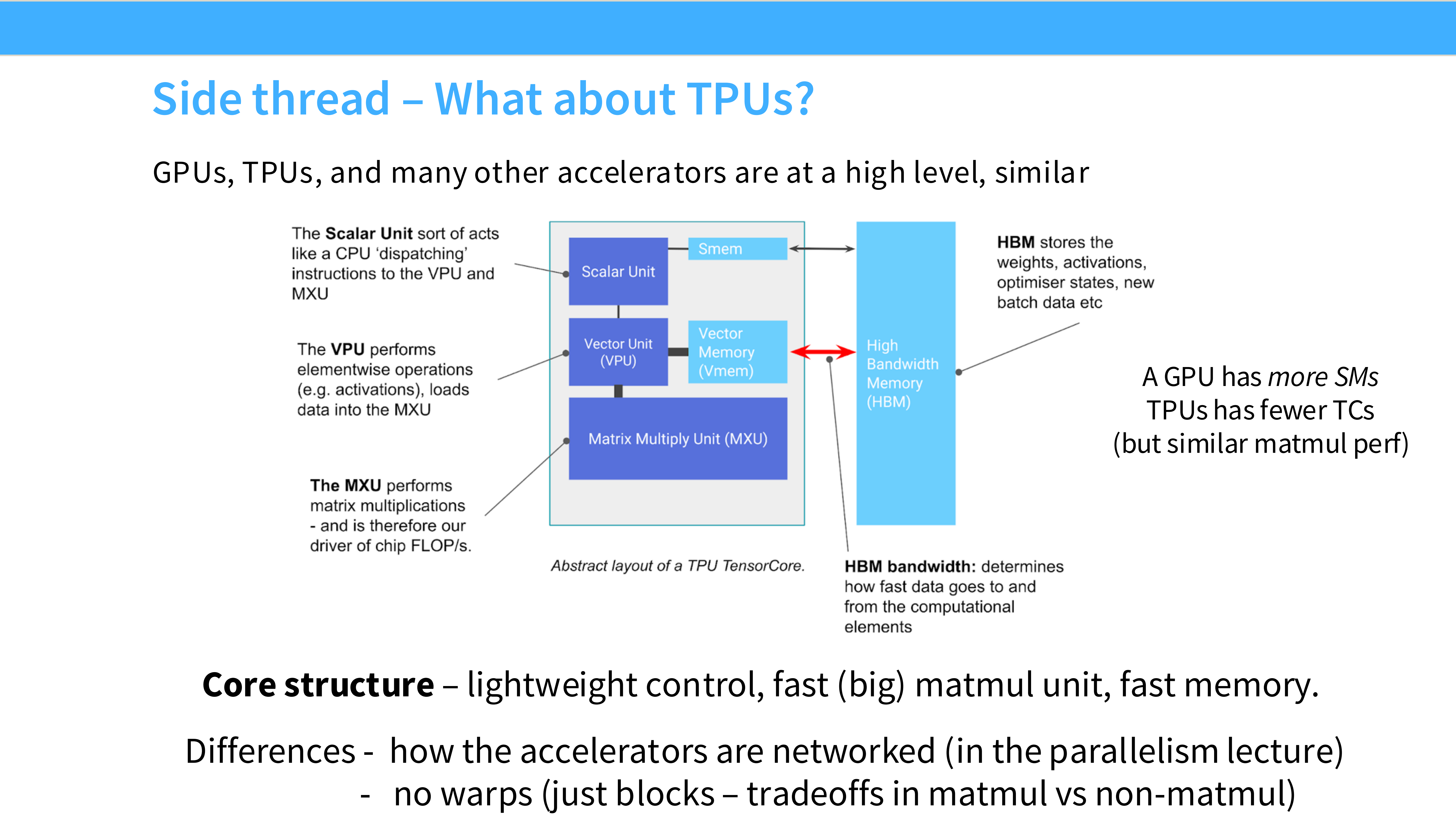
Page 12: 侧记 - 关于 TPU

• 内容解析： TPU (Tensor Processing Unit) 与 GPU 的异同。
  • 核心差异： GPU 有很多个通用的 SM；TPU 则拥有巨大的 **Matrix Multiply Unit (MXU)**，采用脉动阵列架构。
  • 权衡： TPU 牺牲了通用性（Lightweight control），换取了极致的矩阵乘法密度。但在内存带宽（HBM）上，两者面临相似的物理限制。

---

Part 2: 理解 GPU 性能与优化 (Making ML Workloads Fast)

Page 13: Part 2 标题

• 内容解析： 如何让机器学习工作负载在 GPU 上飞快运行？这部分将介绍核心的性能模型和优化技巧。

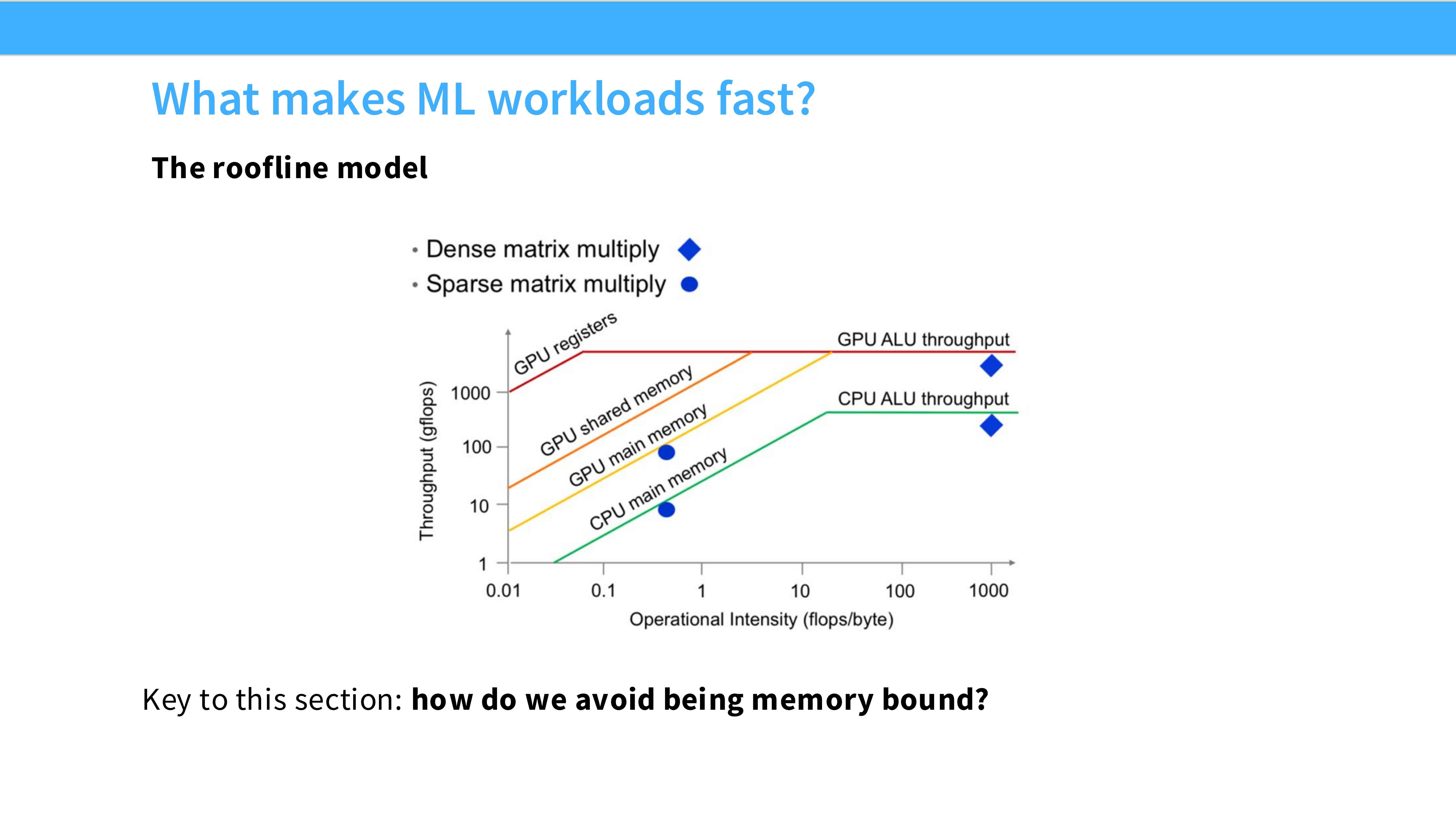
Page 14: 屋顶模型 (The Roofline Model)

• 内容解析： 分析性能的黄金法则。
  • Memory Bound (斜线)： 算术强度 (FLOPs/Byte) 低。GPU 算得快，但数据传输慢，处于“等数据”状态。大多数 Element-wise 操作（如 Activation）在此区域。
  • Compute Bound (平顶)： 算术强度高。数据传输跟得上，瓶颈在于计算单元的峰值性能。大矩阵乘法在此区域。
  • 优化目标： 提高算术强度，向右移动，利用满 GPU 的算力。

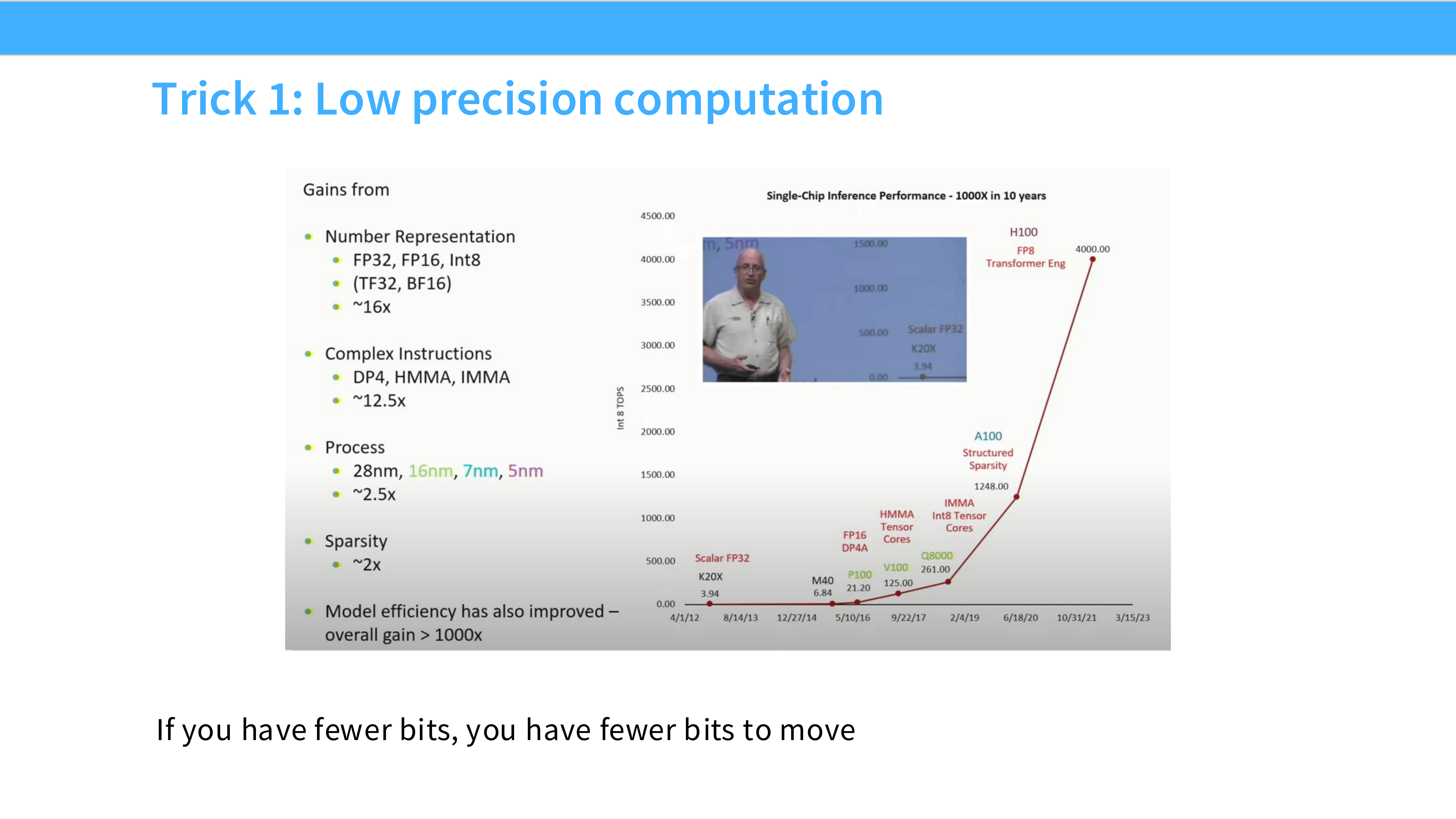
Page 15: 技巧 1 - 低精度计算 (Low Precision)

• 内容解析：
  • 原理： 使用 FP16 (16-bit) 或 INT8 代替 FP32 (32-bit)。
  • 收益： “If you have fewer bits, you have fewer bits to move.” 核心收益不仅仅是计算快了，更重要的是减少了数据搬运量，变相提升了内存带宽利用率。

Page 16: 低精度提升算术强度

• 内容解析： 以 ReLU 为例：
  • FP32: 读 4 字节，写 4 字节，算 1 次。强度 = 1/8 FLOP/Byte。
  • FP16: 读 2 字节，写 2 字节，算 1 次。强度 = 1/4 FLOP/Byte。
  • 结论： 切换到 FP16，算术强度翻倍，性能上限（在 Memory Bound 区域）直接翻倍。

Page 17: Tensor Cores

• 内容解析：
  • 定义： 现代 GPU (Volta+) 引入的专用电路，专门用于加速矩阵乘法 ($D = A \times B + C$)。
  • 威力： 在混合精度下，Tensor Cores 的吞吐量是普通 CUDA Cores 的 10 倍以上。
  • 影响： 这让矩阵乘法变得极快，使得非矩阵操作（如 Softmax, LayerNorm）更容易成为性能瓶颈。

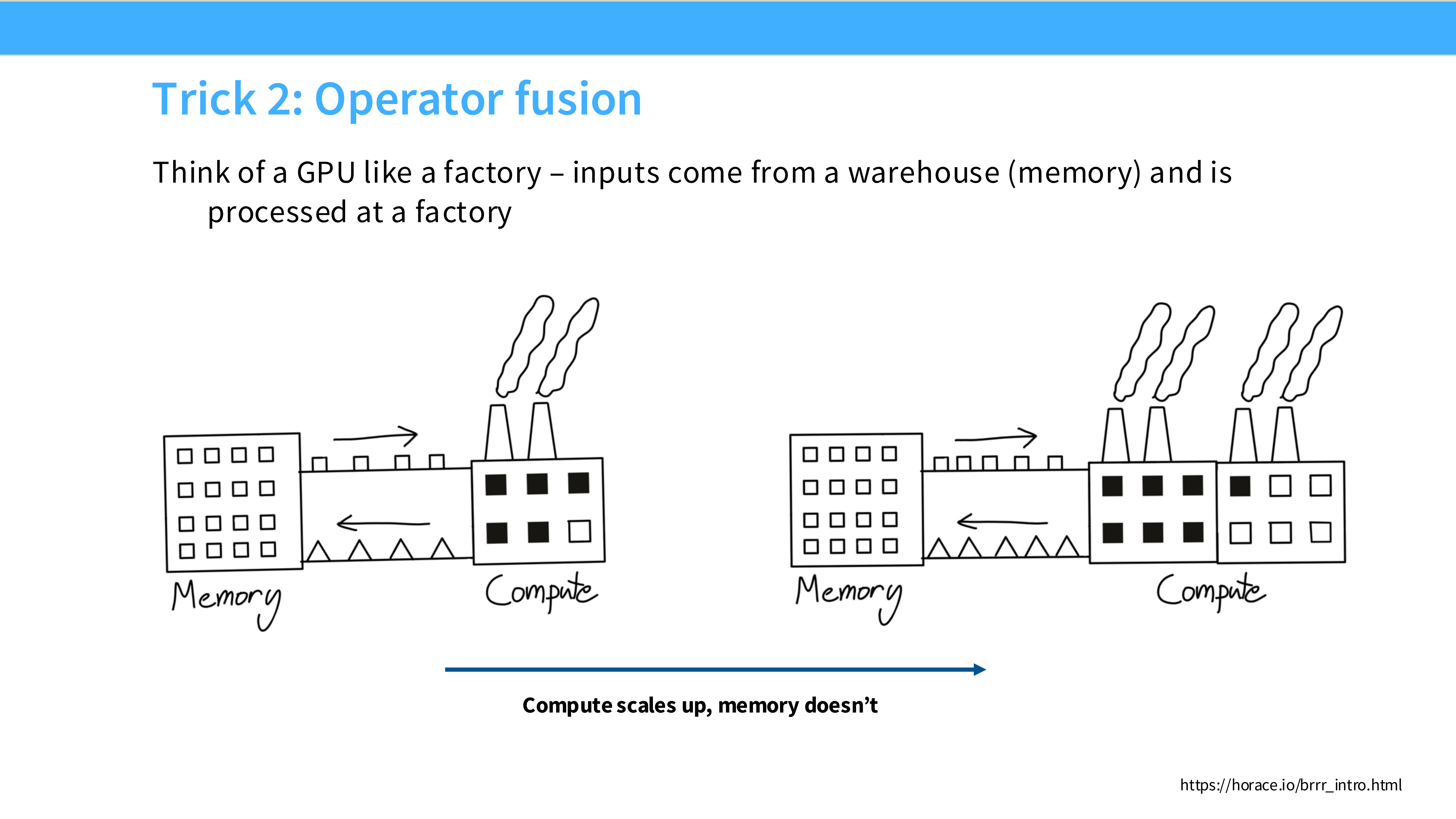
Page 18: 技巧 2 - 算子融合 (Operator Fusion)

• 内容解析：
  • 左图 (无融合)： 像一个低效的工厂。每做一步（Add, Mul），都要把产品运回仓库（显存），再运回来做下一步。
  • 右图 (融合)： 流水线作业。数据读入寄存器后，一次性完成一系列计算（Add + Mul + Relu），最后只写回一次。
  • 核心： 最小化 HBM 的读写次数。

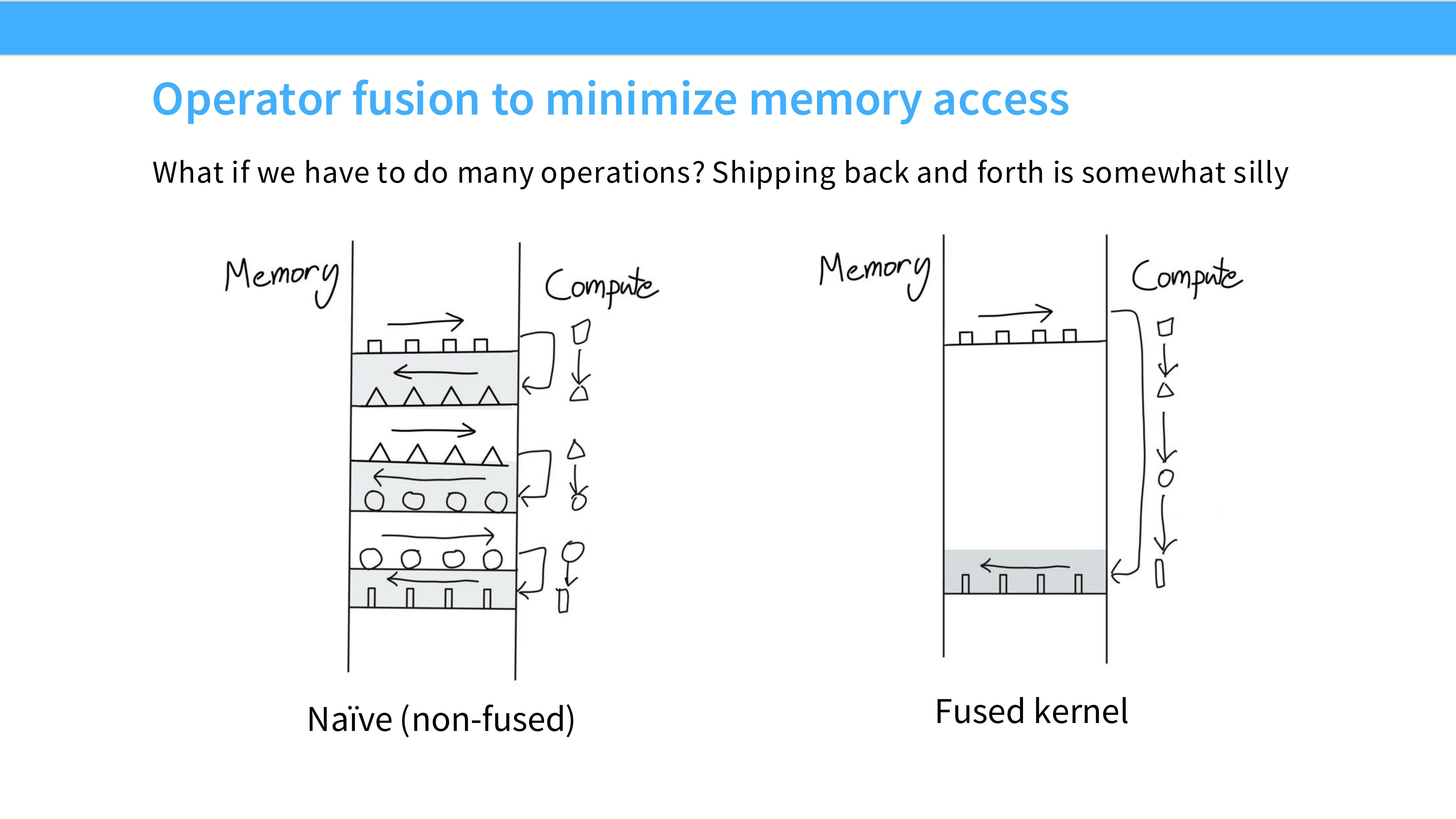
Page 19: 融合的内存视角

• 内容解析： 对比图解。
  • Naive: 多个 Kernel 串行，中间结果频繁读写 HBM，带宽压力大。
  • Fused Kernel: 一个 Kernel 完成所有工作，中间结果在寄存器或 Shared Memory 中传递，极其高效。

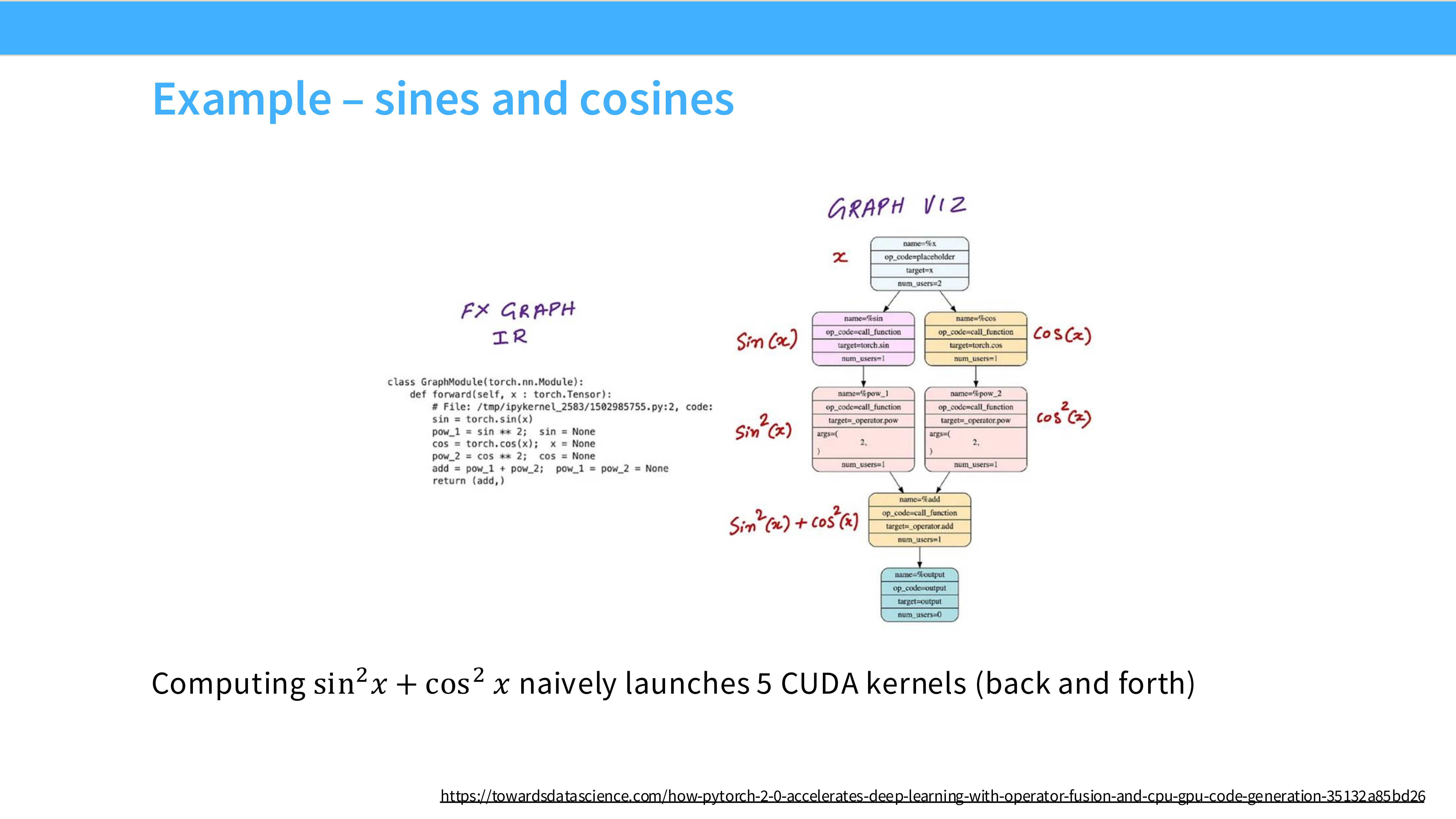
Page 20: 融合案例 - Sin/Cos

• 内容解析： 计算 $\sin^2(x) + \cos^2(x)$。
  • 如果不融合，需要启动 5 个 Kernel，反复搬运数据。
  • 融合后，只需 1 个 Kernel，数据只读写一次。

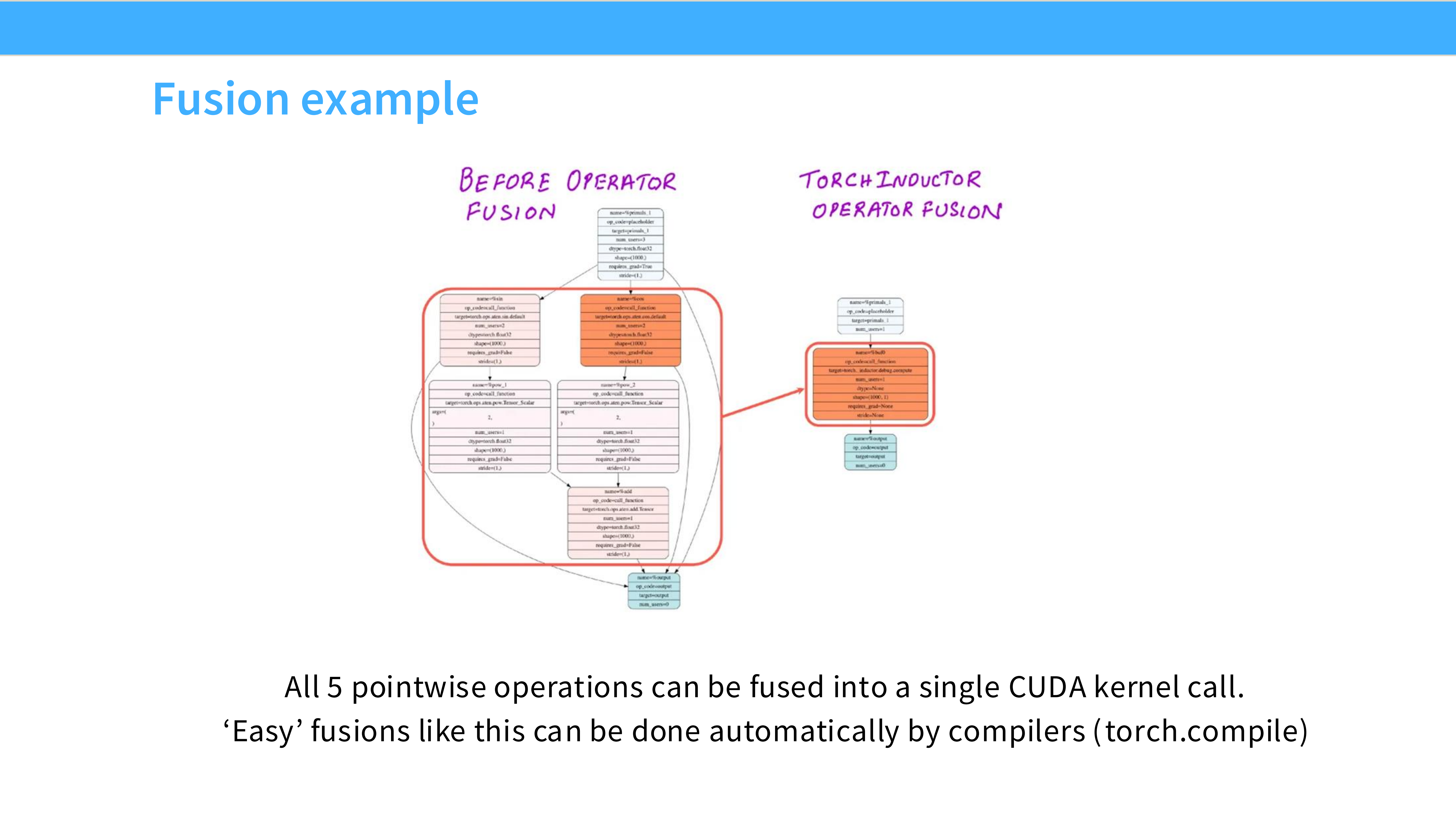
Page 21: 编译器自动融合

• 内容解析：
  • TorchInductor: PyTorch 2.0 的编译器。它可以自动分析计算图，将多个 Pointwise 操作“融合”成一个单一的 CUDA Kernel，无需手写 CUDA 代码。

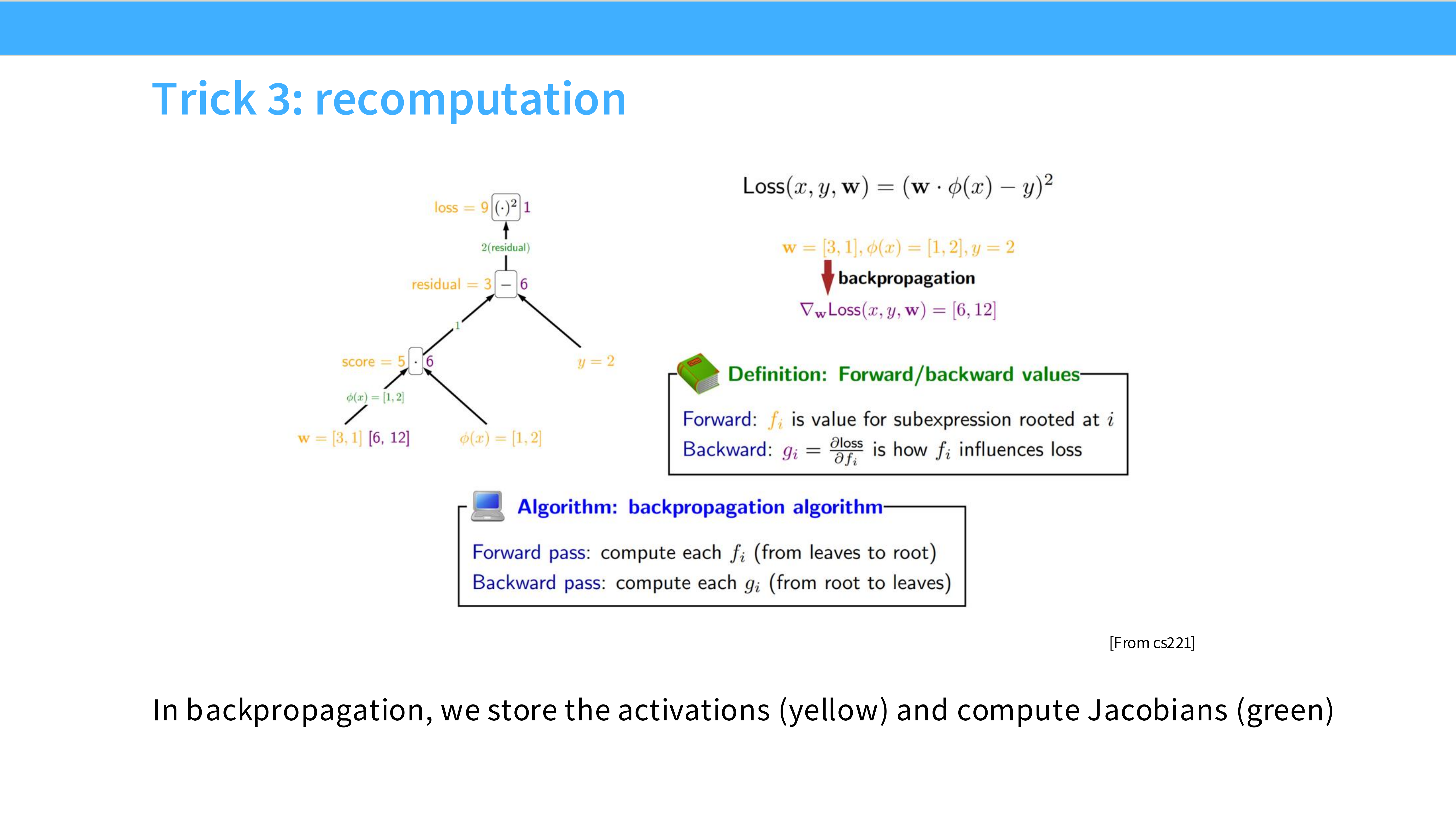
Page 22: 技巧 3 - 重计算 (Recomputation)

• 内容解析：
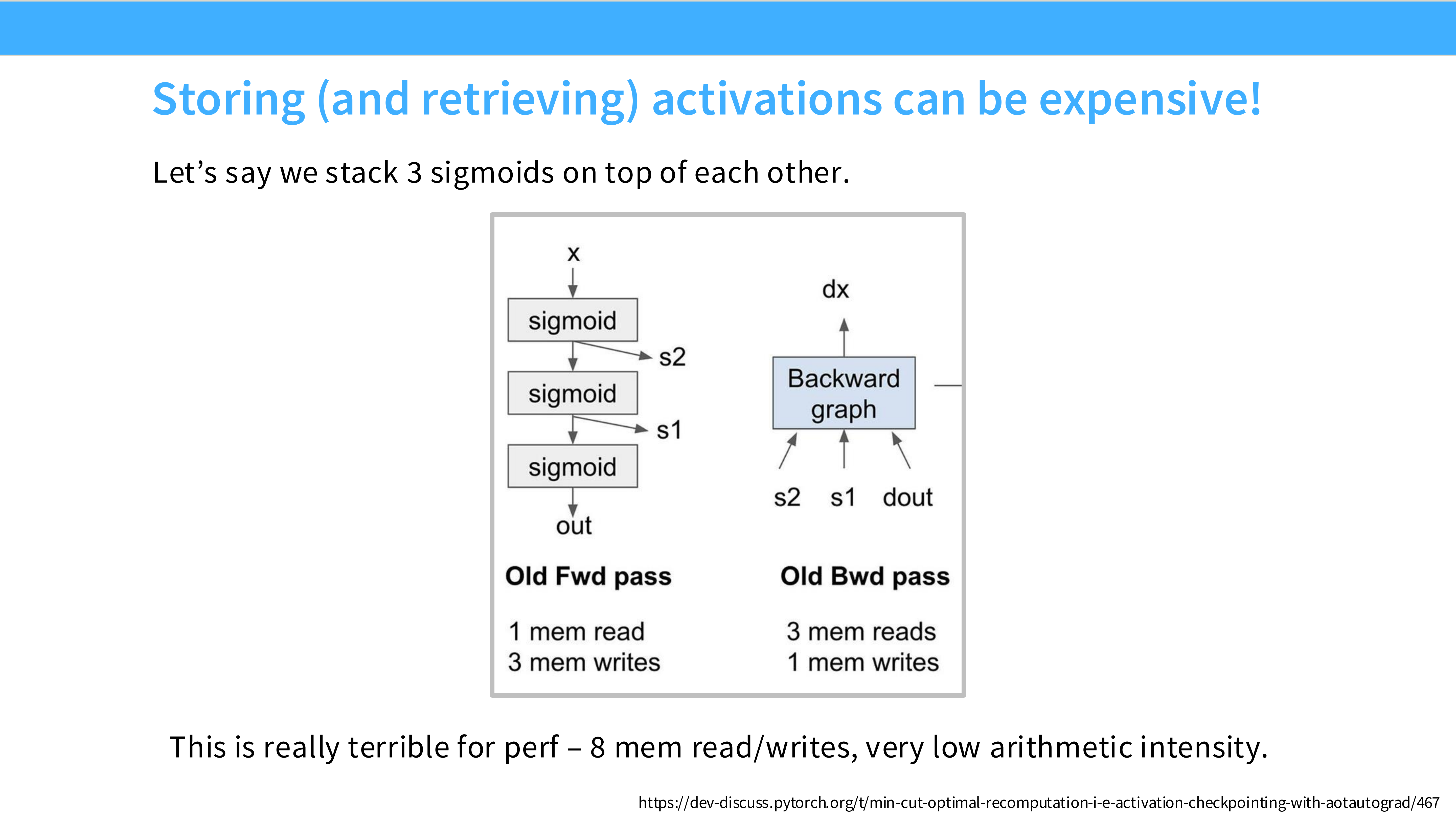
  • 问题： 显存不够存下所有激活值（Activations）。
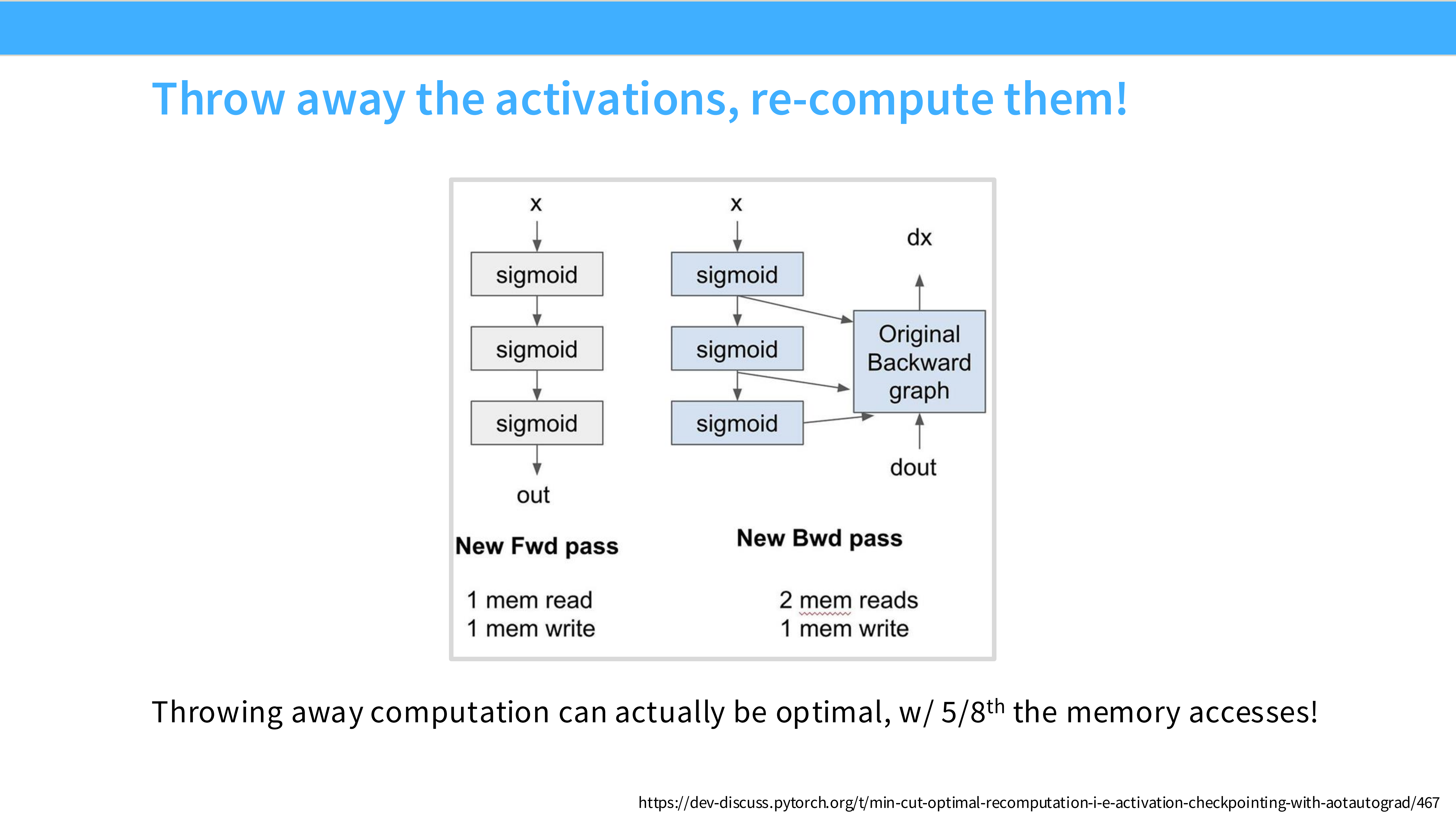
  • 策略： Throw away the activations, re-compute them! 在反向传播时，不读取缓存的激活值，而是重新计算一遍。
  • 逻辑： 因为 Compute (FLOPs) 很便宜且快，Memory (HBM) 很贵且慢。在 Memory Bound 场景下，重计算往往比去 HBM 读数据还要快。

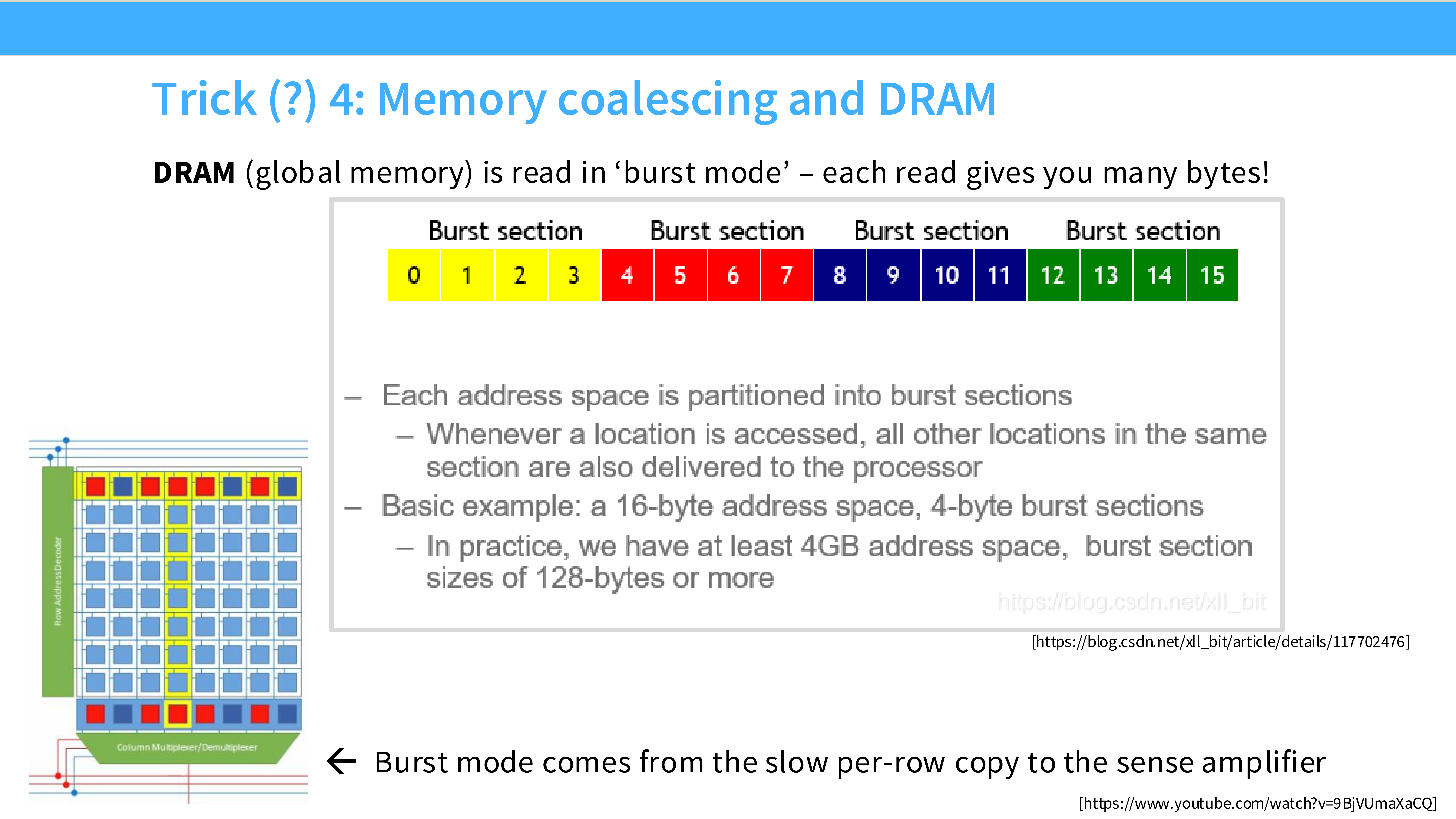
Page 23: 技巧 4 - 内存合并 (Memory Coalescing)

• 内容解析：
  • DRAM 特性： 内存读取是 Burst Mode（爆发模式）。即使你只请求 1 个字节，DRAM 也会发给你一块连续数据（例如 128 字节）。
  • 隐喻： 就像快递，不会送一根牙签，至少是一个盒子。

Page 24: 什么是 Coalesced Loads

• 内容解析：
  • 图示： 线程 0-15 依次访问地址 0-15。
  • 效果： 硬件将这 16 个请求合并为 1 个 内存事务。这是最高效的访问模式。

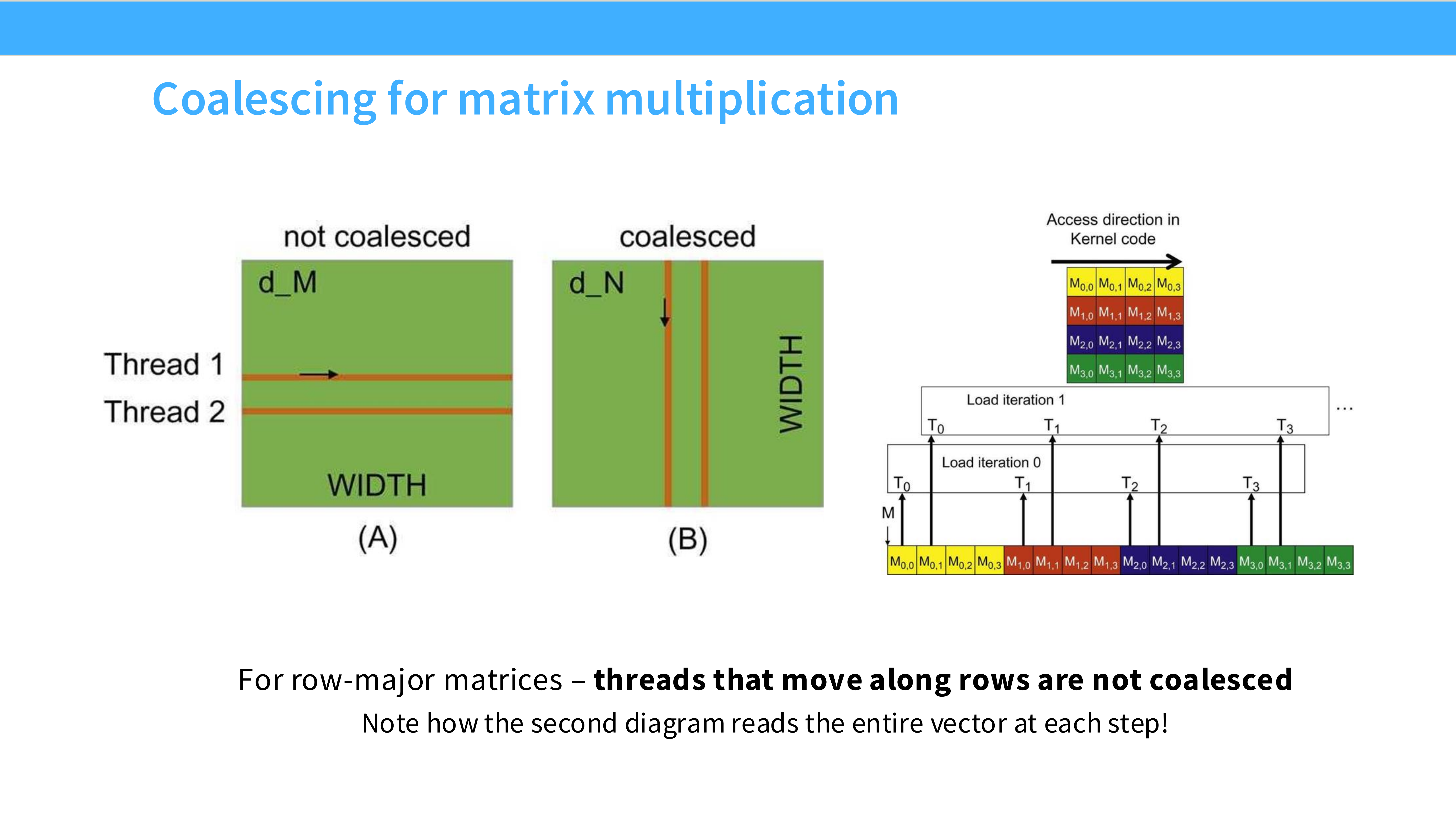
Page 25: 未合并的代价

• 内容解析：
  • 左图 (Unaligned/Strided)： 线程跳跃访问。为了读几个有用数据，不得不触发多次 Burst，传输了大量无用的红色数据块。带宽浪费严重。
  • 右图 (Aligned)： 高效利用带宽。
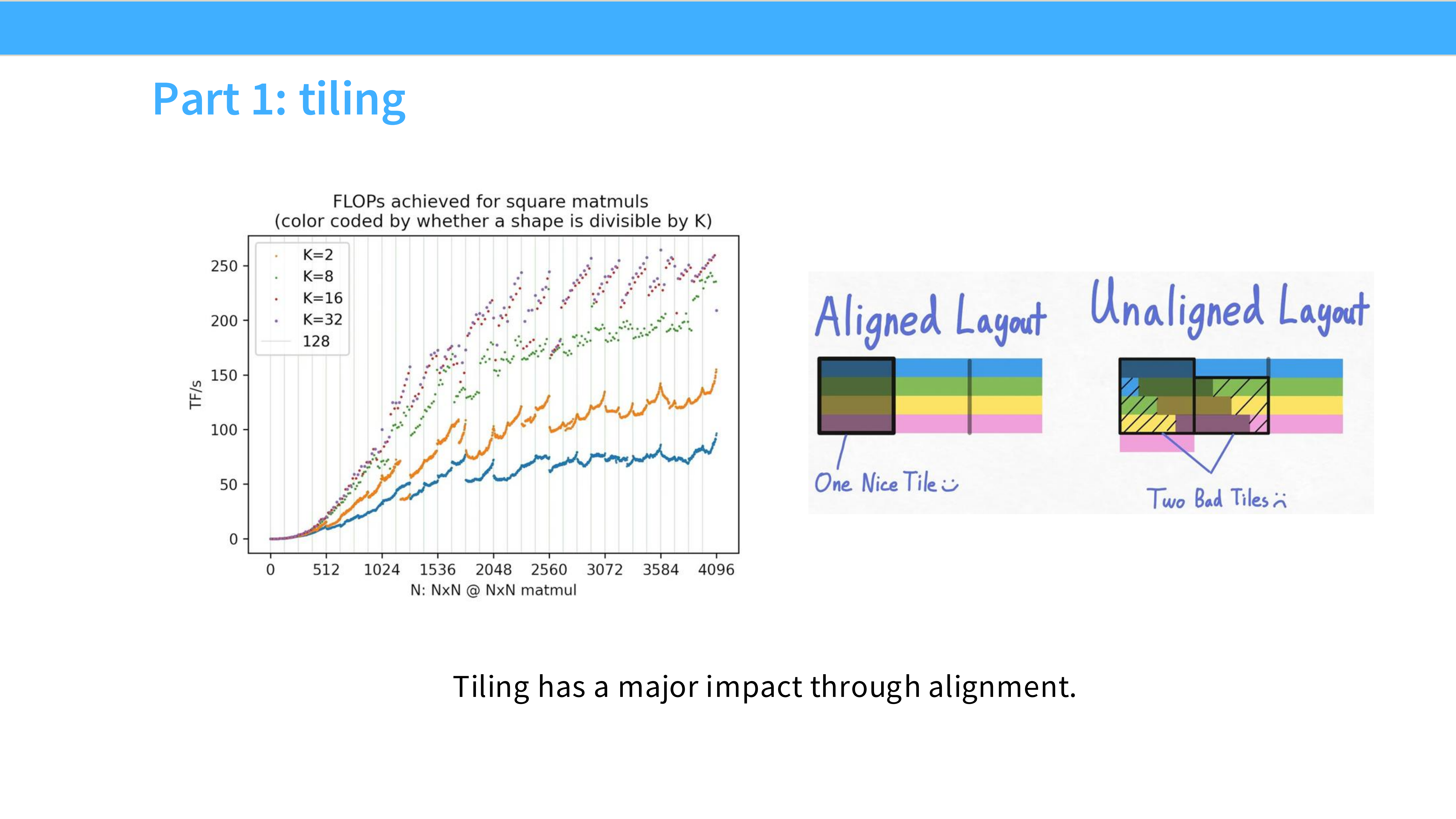
  • 总结： “One Nice Tile vs Two Bad Tiles”。

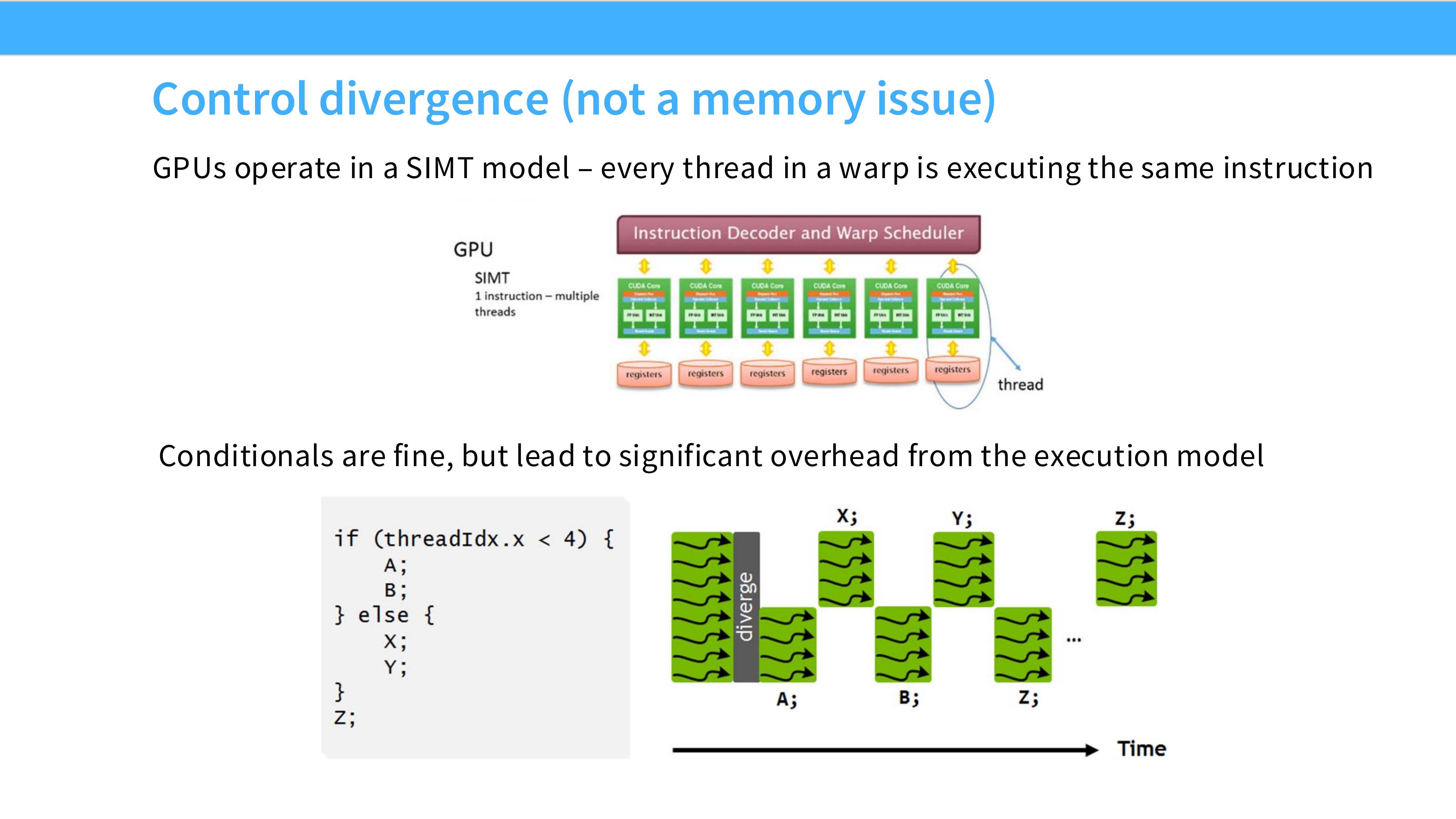
Page 26: 控制流分歧 (Control Divergence)

• 内容解析：
  • 问题： 代码中有 if-else。
  • 机制： 由于 SIMT 特性，如果 Warp 内部分线程走 if，部分走 else，硬件会串行化执行——先跑 if（另一半线程空转等待），再跑 else。
  • 影响： 这不是内存问题，而是并行效率问题，会导致算力利用率减半。

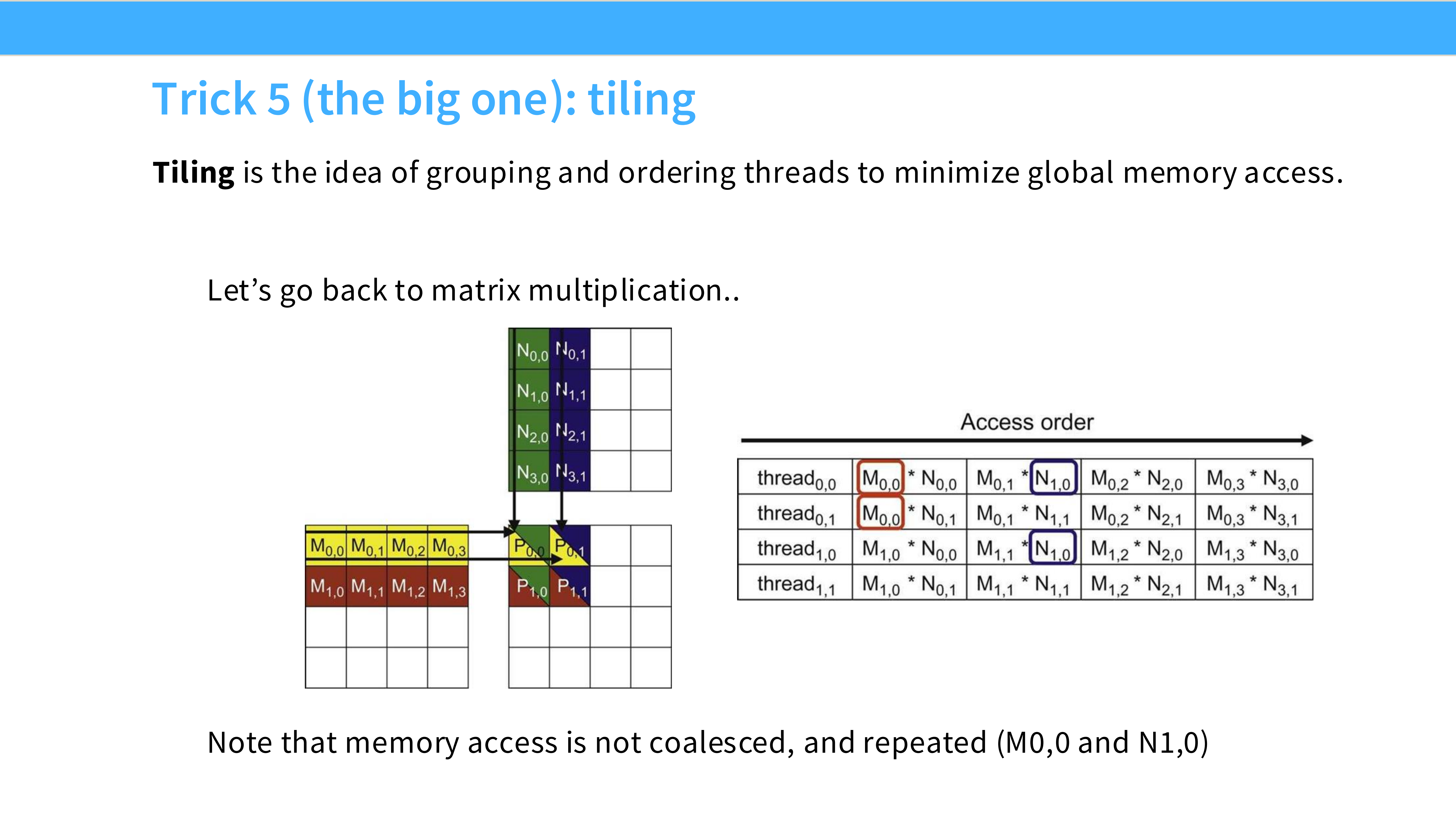
Page 27: 技巧 5 - 分块 (Tiling) [最重要]

• 内容解析：
  • 概念： 将大矩阵切分成小块（Tiles）。
  • 目的： 利用 Shared Memory (SRAM) 这种高速片上内存。将小块数据加载到 SRAM，让线程反复在 SRAM 上读取数据进行计算，从而减少对慢速 HBM 的访问。

Page 28: Tiling 的数学原理

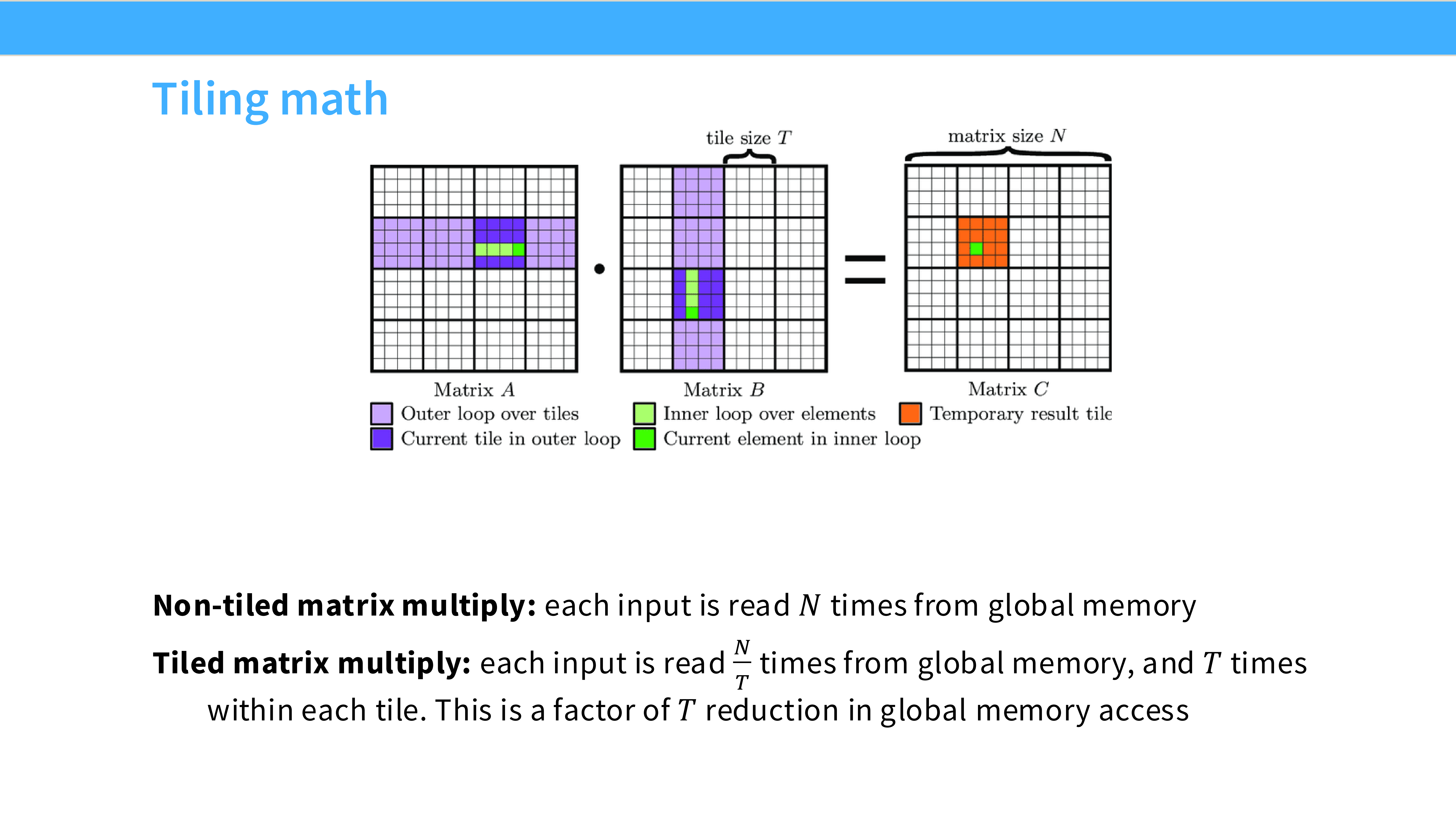
• 内容解析：
  • Non-tiled: 计算 $C$ 的每个元素都要从 HBM 读取 $A$ 的一行和 $B$ 的一列。每个数据被重复从 HBM 读取 $N$ 次。
  • Tiled: 每个数据只从 HBM 读取 $N/T$ 次（$T$ 是 Tile 大小）。
  • 收益： 内存访问量减少了 $T$ 倍。这是矩阵乘法高效的根本原因。

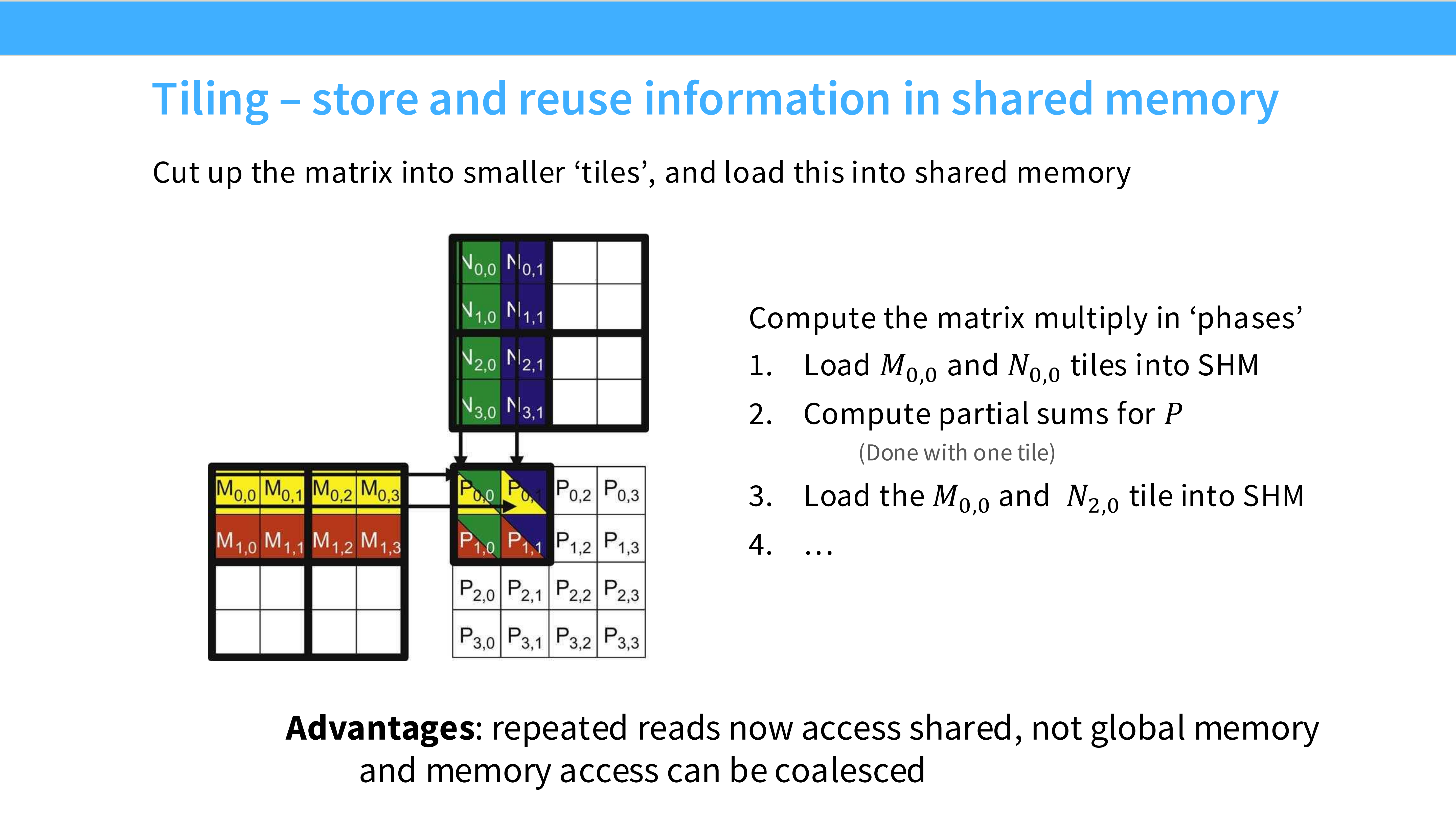
Page 29: Tiling 与 Shared Memory

• 内容解析： 流程演示：
  1. 协作将 $M_{0,0}$ 和 $N_{0,0}$ 块从 HBM 加载到 Shared Memory。
  2. 线程在 Shared Memory 上进行高速计算。
  3. 加载下一块。
  • 通过这种方式，大部分内存访问都发生在高速的 SRAM 上。

Page 30: Tiling 的复杂性 1 - 边界问题

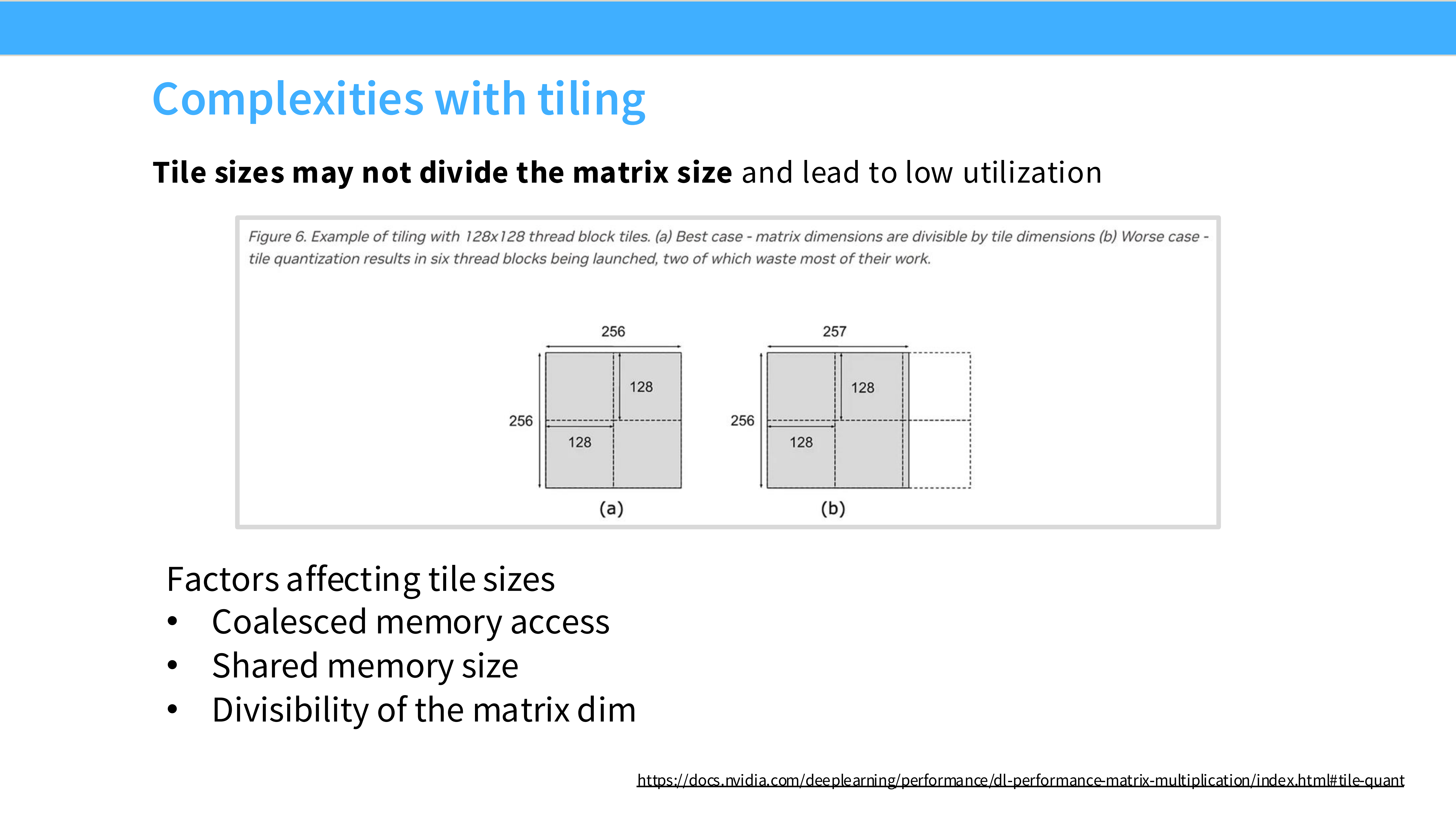
• 内容解析：
  • 如果矩阵大小不能被 Tile 大小整除，边缘会多出一部分。
  • 需要处理 Padding 或者在代码中加 边界检查，这会导致利用率下降（部分线程空转）。

Page 31: Tiling 的复杂性 2 - 对齐问题

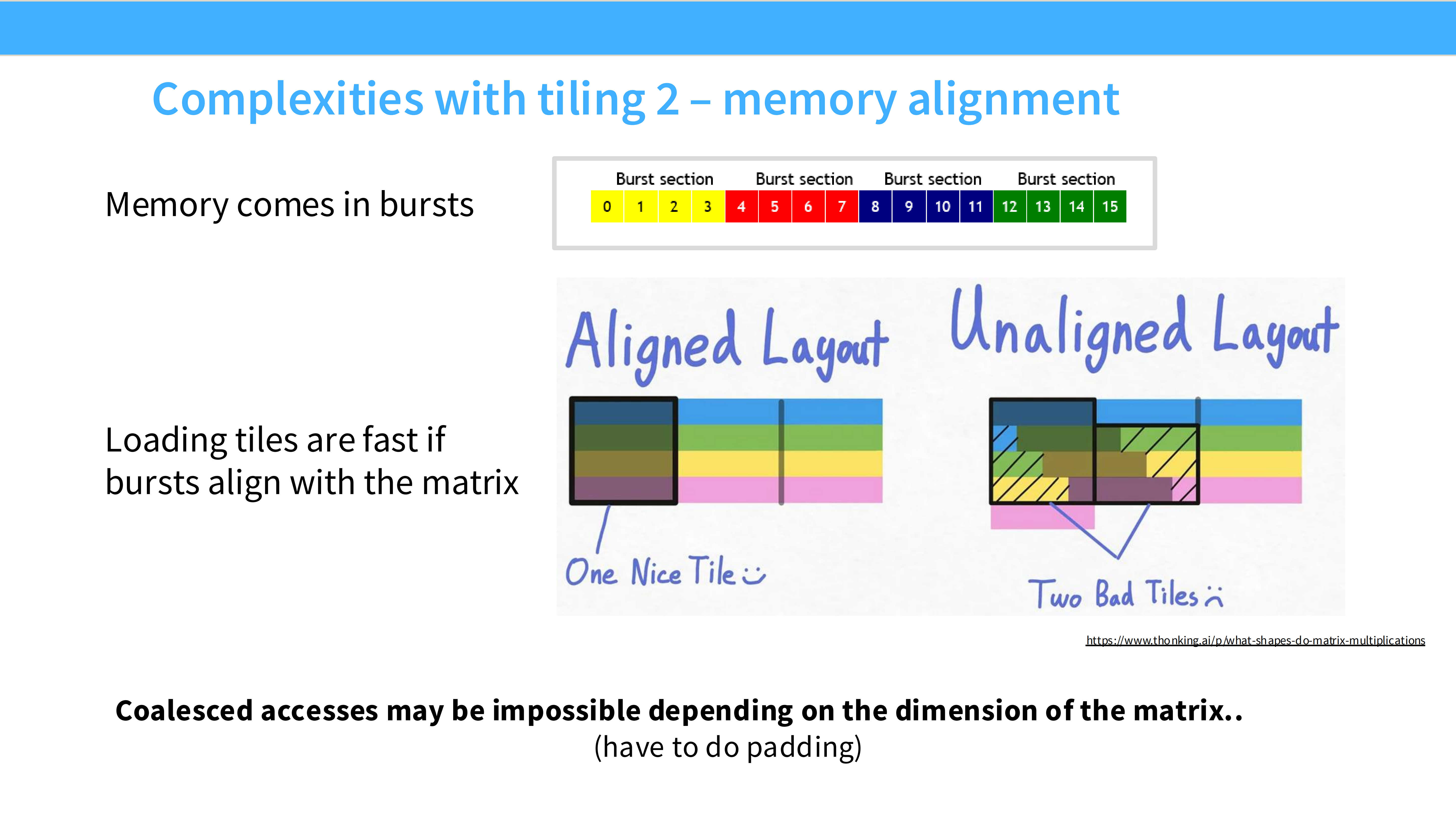
• 内容解析：
  • Aligned: 完美对齐，利用 Coalescing。
  • Unaligned: 数据起始位置未对齐，导致一次 Tile 读取需要跨越多个内存块，带宽减半。

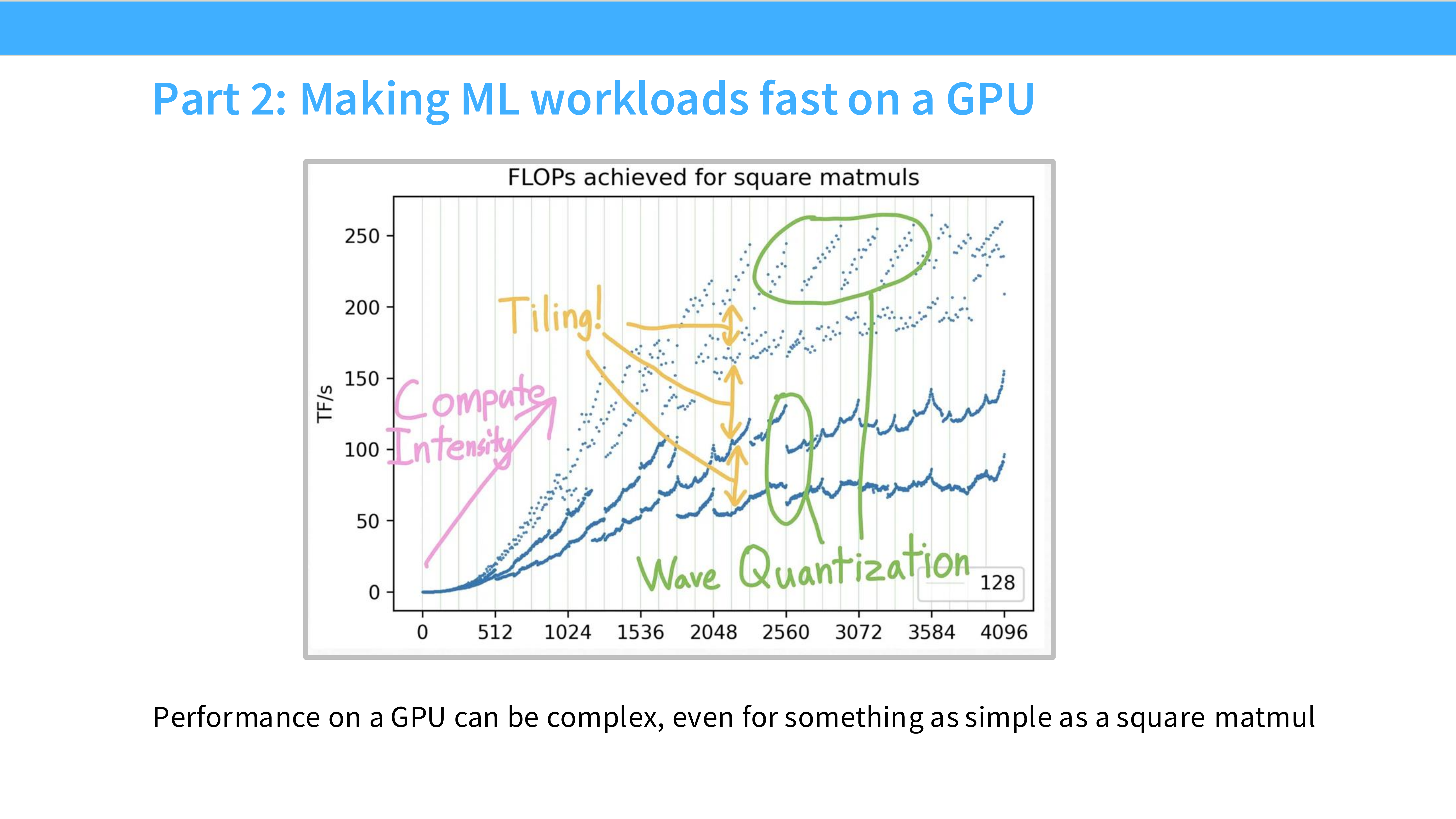
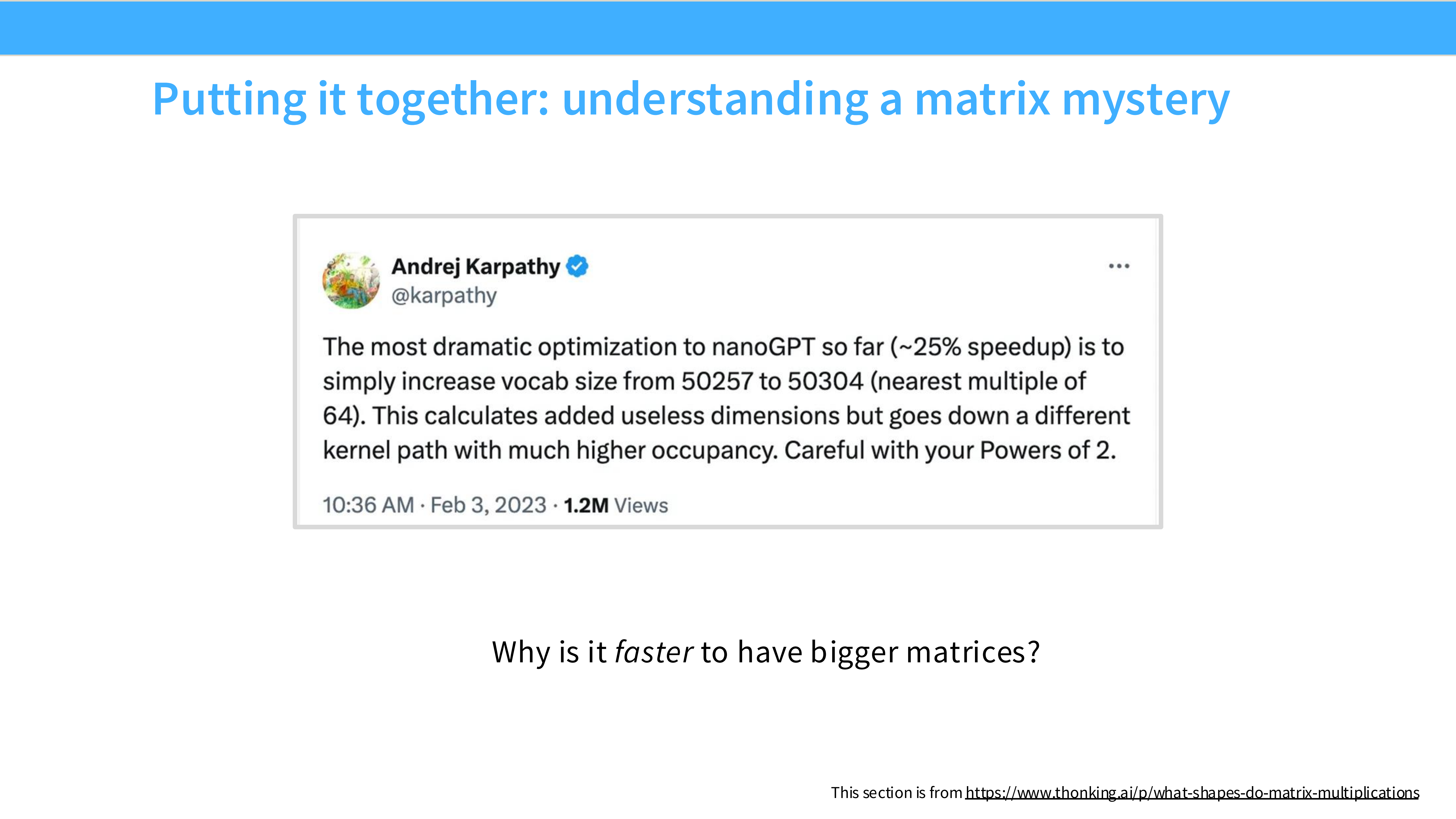
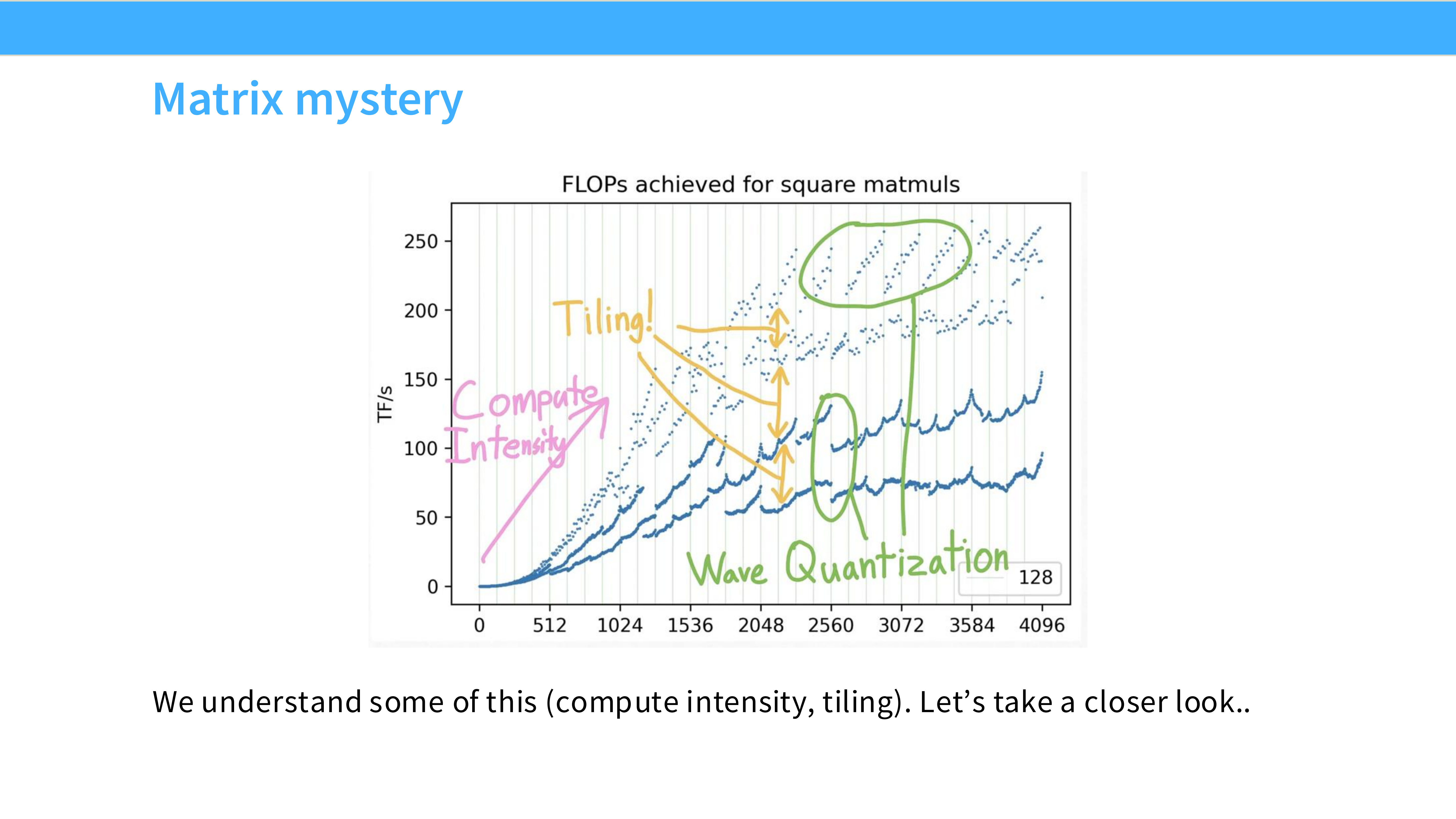
Page 32: 矩阵性能之谜

• 内容解析： 展示了一个锯齿状的性能曲线。为什么矩阵大小从 2048 增加到 2049，性能会突然下降？

Page 33: 波浪量化 (Wave Quantization)

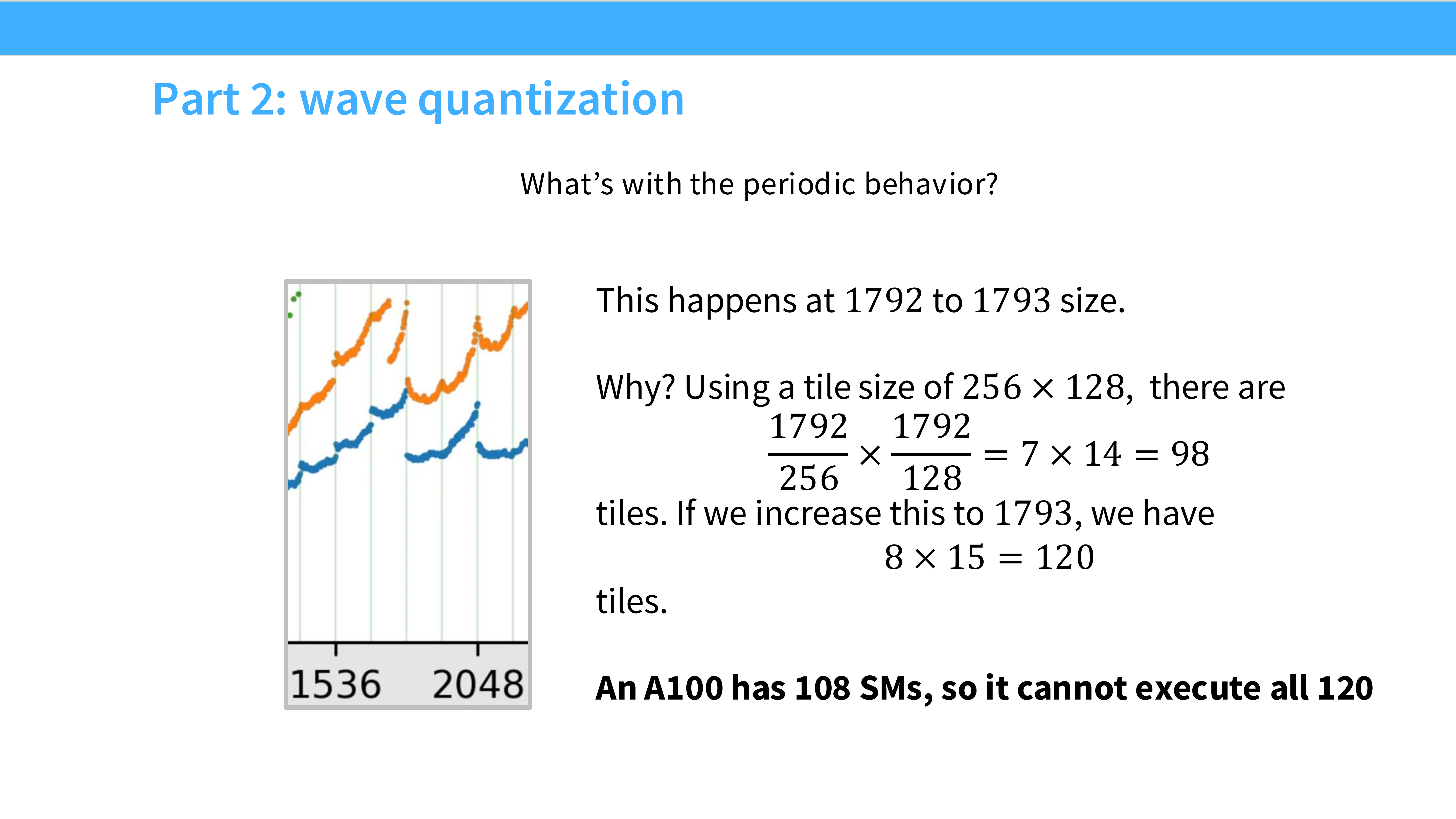
• 内容解析： 解释了锯齿原因。
  • GPU 的 SM 数量是固定的（如 108 个）。
  • Wave Effect: 如果任务块数量是 108，GPU 刚好一波跑完，效率 100%。
  • Tail Effect: 如果任务块是 109，前 108 个跑完后，剩下 1 个块还需要占用一整波的时间，此时 107 个 SM 是空闲的。
  • 结论： 矩阵大小最好是 SM 数量的整数倍。

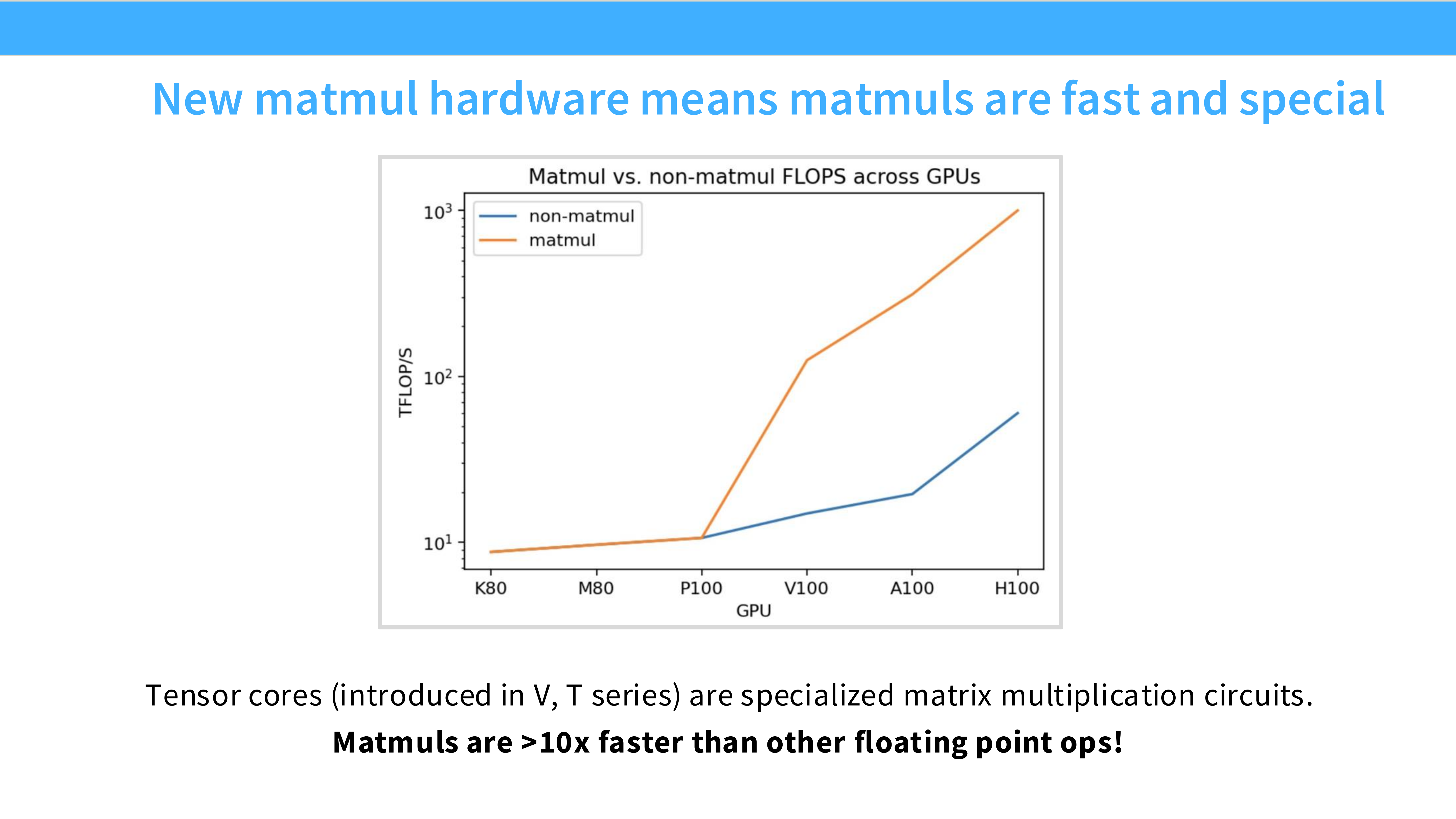
Page 34: 新一代硬件 (Matmuls are fast)

• 内容解析：
  • 由于 Tensor Cores 的存在，矩阵乘法现在非常快（比其他操作快 10 倍）。
  • 现在的瓶颈往往转移到了那些不能利用 Tensor Core 的操作上。

Page 35: 历史回顾

• 内容解析： 在 CUDA 出现之前，研究人员不得不把矩阵运算伪装成图形渲染任务（Graphics Hardware）来利用 GPU。现在我们有了专门的工具。

Page 36: Part 2 总结

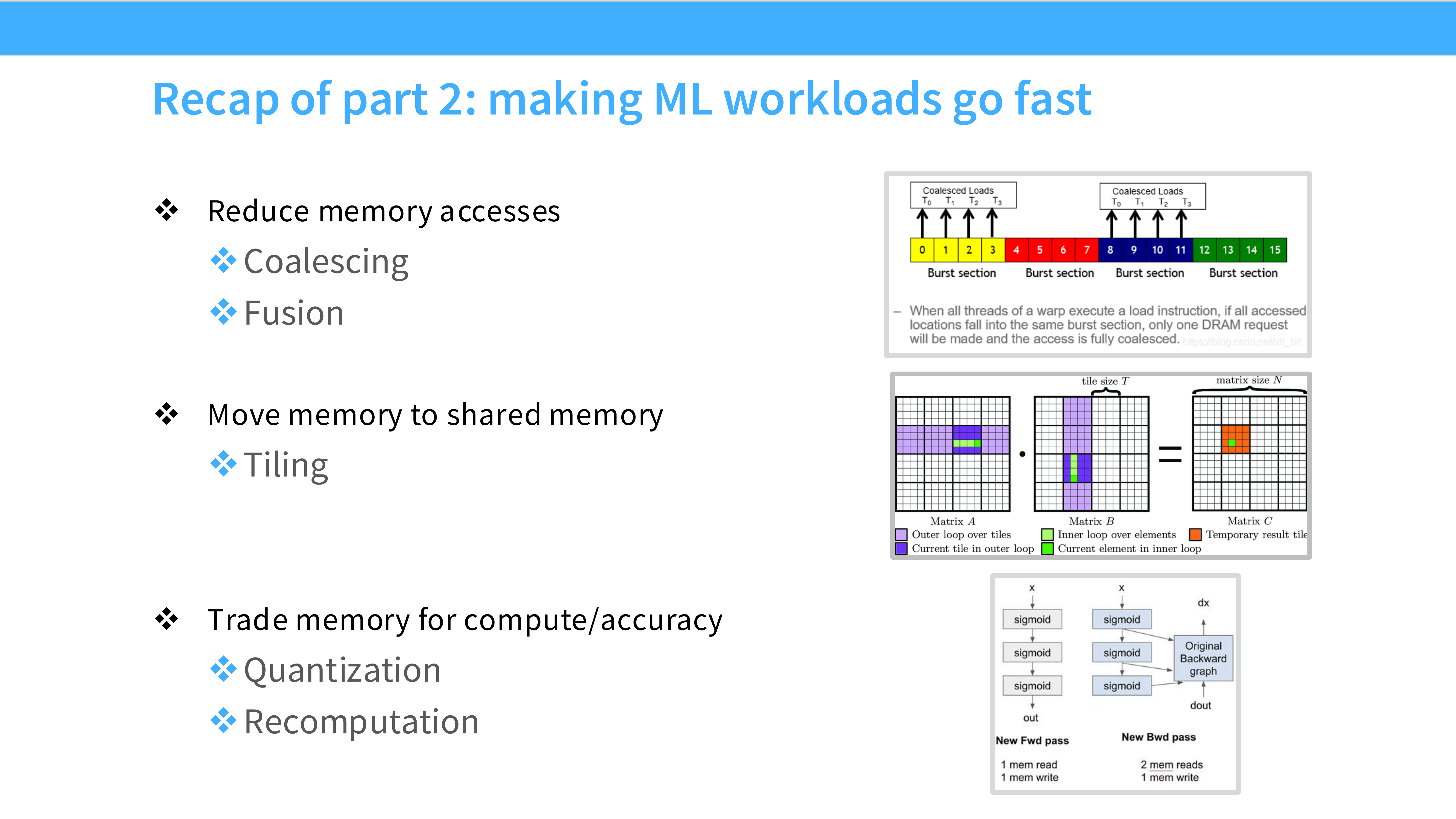
• 内容解析： 让 ML 负载变快的三个关键：
  1. Reduce memory access: 通过 Coalescing 和 Fusion。
  2. Shared memory: 通过 Tiling 复用数据。
  3. Compute trade-offs: 低精度、重计算。

---

Part 3: 实战案例 - FlashAttention (Putting it all together)

Page 37: Part 3 标题

• 内容解析： 这一部分将前面的理论知识综合运用，解构 FlashAttention。这是一个完美的案例，展示了如何通过硬件感知（IO-aware）的算法设计来突破性能瓶颈。

Page 38: Attention 计算回顾

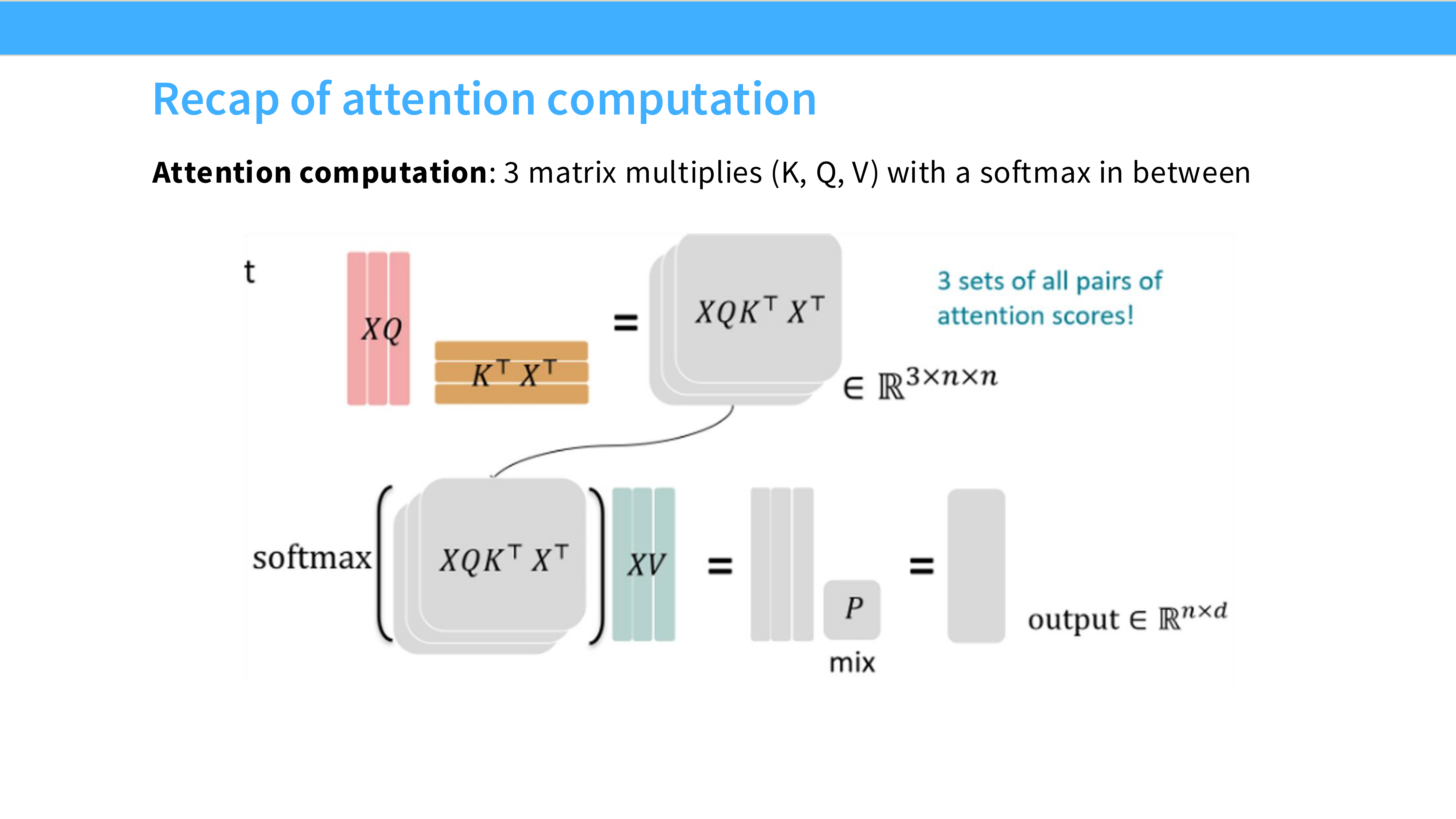
• 内容解析：
  • 公式： $Attention(Q, K, V) = Softmax(QK^T)V$。
  • 流程： 包含三个矩阵乘法。中间会生成一个 $N \times N$ 的矩阵（Attention Scores）。
  • 痛点： $N \times N$ 矩阵读写量巨大，且显存占用是平方级 $O(N^2)$。这导致长序列训练极其缓慢且显存不足。

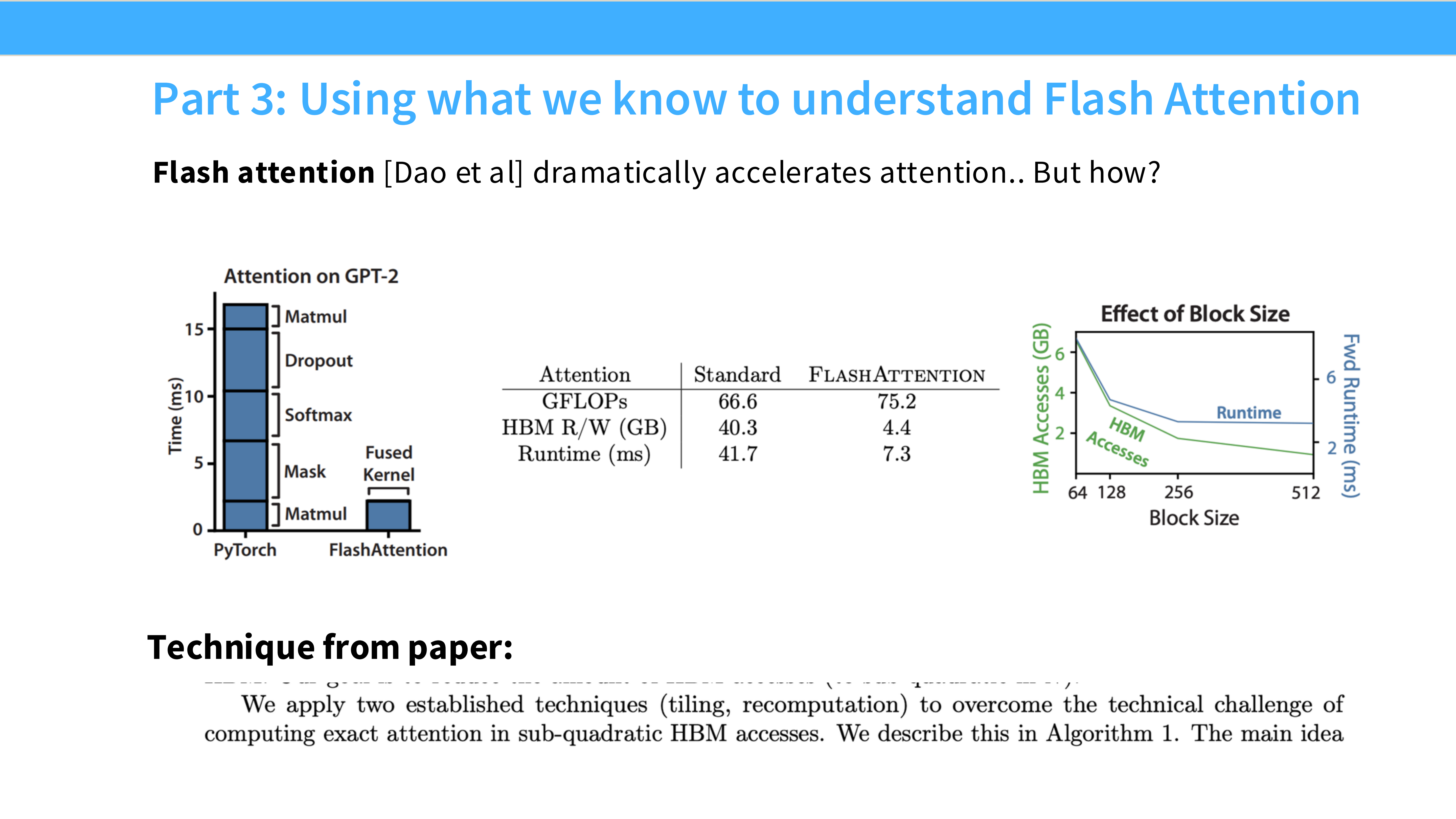
Page 39: FlashAttention 的效果

• 内容解析：
  • Runtime (左图)： 随着 Block Size 增加，FlashAttention 速度显著快于标准 Attention。
  • Memory (右图)： 显存占用从平方级降低到了线性级。
  • 核心思想： Tiling (分块) + **Recomputation (重计算)**。避免物化（Materialize）巨大的 $N \times N$ 矩阵。

Page 40: Tiling Part 1 - 矩阵乘法

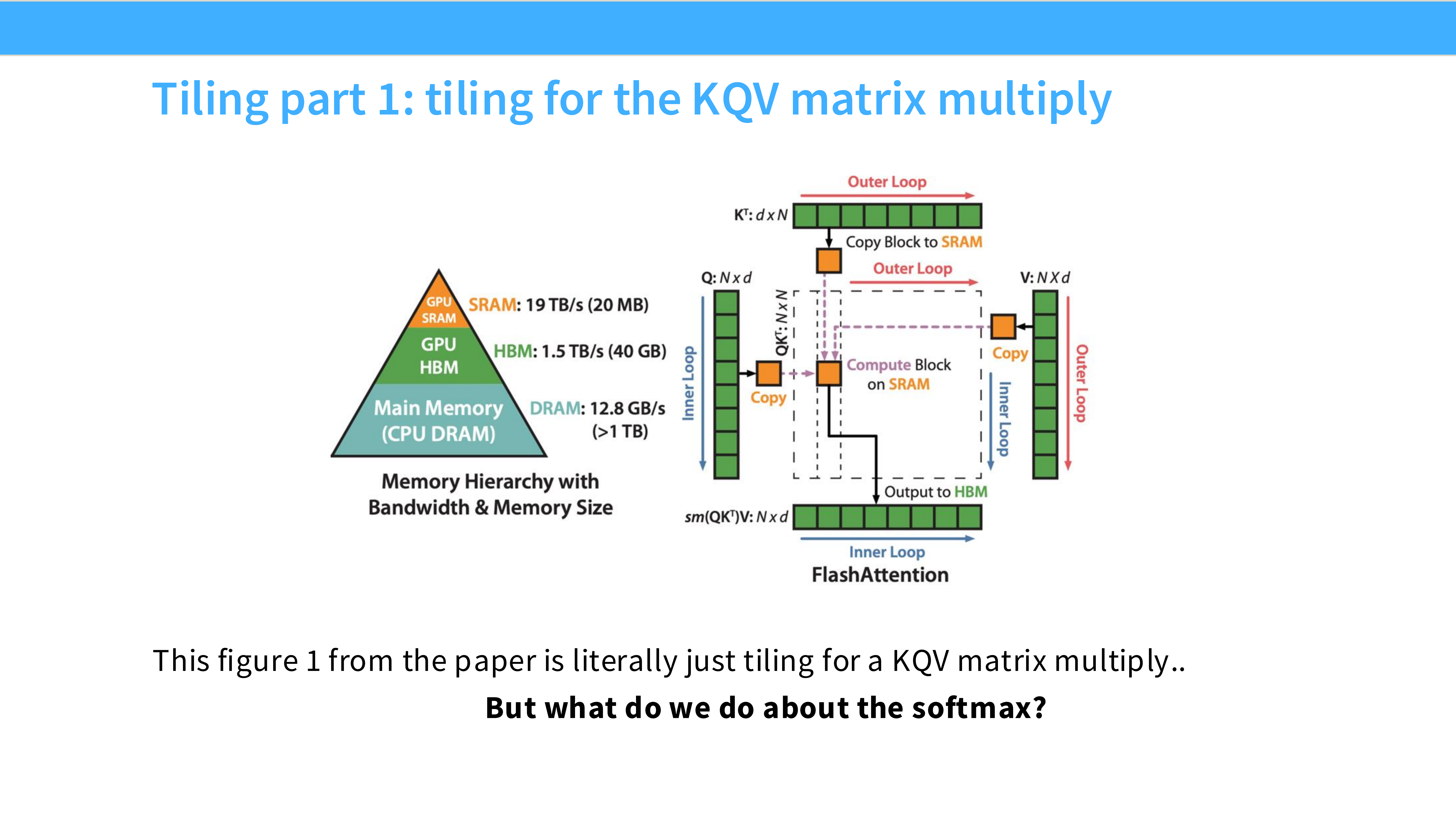
• 内容解析：
  • 这部分利用了标准的 Tiling 技巧。将 $Q, K, V$ 矩阵切分成小块。
  • 将小块加载到 SRAM，计算局部的 $Q \times K^T$。这部分比较直观。

Page 41: Tiling Part 2 - Softmax 的难题

• 内容解析：
  • 挑战： Softmax 是一个全局操作，需要一整行的 Max 和 Sum 才能进行归一化。
  • 困境： 如果我们把矩阵切块了，在计算当前块时，无法预知后续块的数值，因此无法知道全局最大值，也就无法直接计算 Softmax。

Page 42: 在线 Softmax (Online Softmax)

• 内容解析：
  • 这是 FlashAttention 的算法创新。引用了 Mikailov 2018 的论文。
  • 技巧： **Telescoping Sum Trick (伸缩和)**。
  • 原理： 维护局部的 max 和 sum。当处理下一个块时，利用数学公式更新全局统计量，并动态修正之前计算出的结果。
  • 意义： 这使得 Softmax 可以 Tile-by-tile 计算，无需一次性生成整个大矩阵。

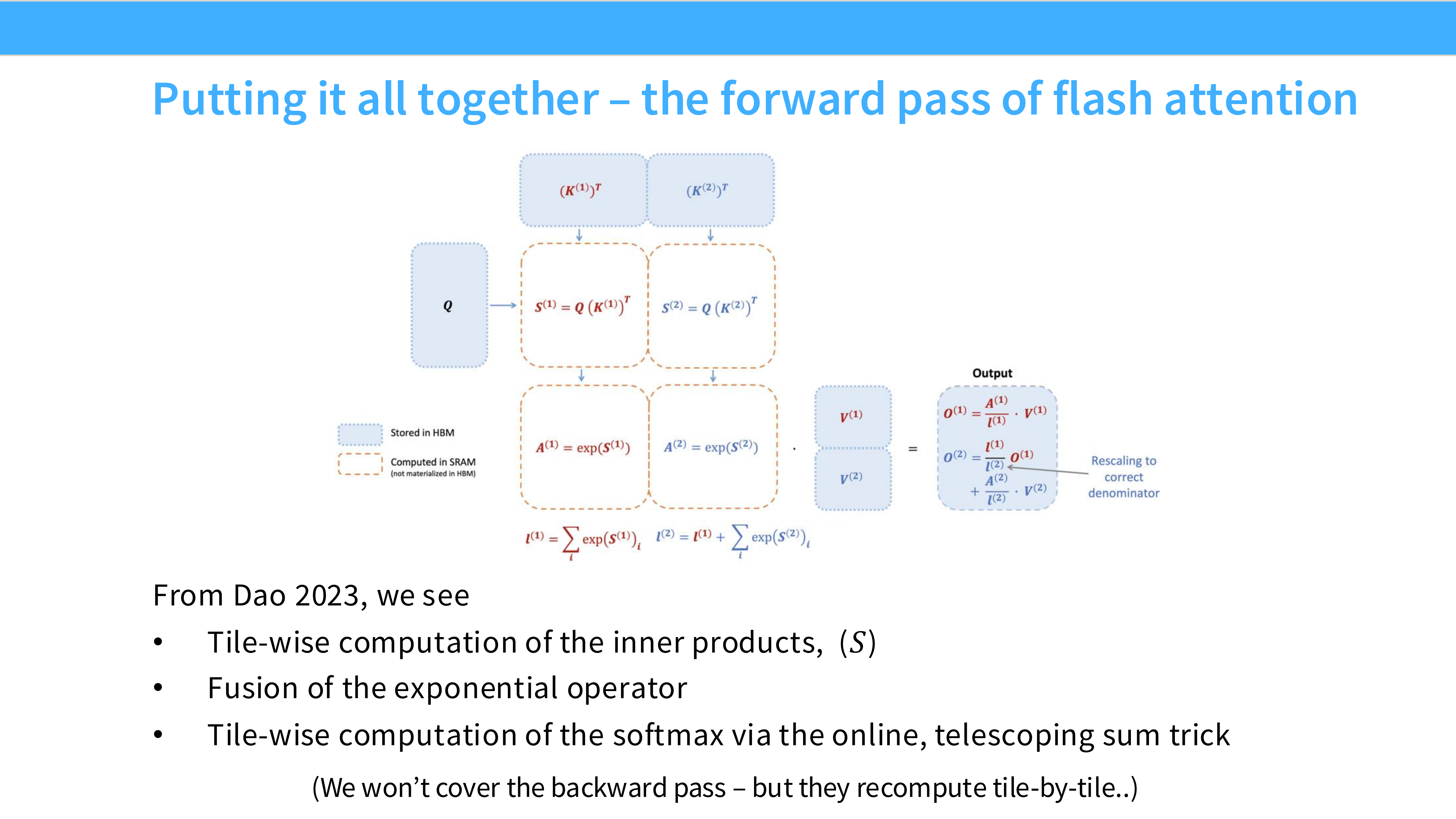
Page 43: 完整的 FlashAttention 前向传播

• 内容解析： 这是 FlashAttention 的核心流程图。
  1. Outer Loop: 遍历 $K, V$ 的块。
  2. Inner Loop: 遍历 $Q$ 的块。
  3. SRAM 计算: 在 SRAM 中计算 $S = QK^T$，更新 Online Softmax 统计量，计算 $O = SV$。
  4. Output: 将结果写回 HBM。
  • 关键： 巨大的 Attention 矩阵从未在 HBM 中完整存在过，全程在 SRAM 中流转并被丢弃。

Page 44: 课程总结 (Recap of Attention)

• 内容解析：
  • 回顾了 Attention 计算的三个矩阵乘法和中间的 Softmax。
  • 强调了 $N \times N$ 矩阵带来的 IO 瓶颈。

Page 45: IO 复杂度分析 (IO Complexity)

• 内容解析：
  • 标准 Attention: IO 复杂度是 $O(N^2)$。
  • FlashAttention: 通过 Tiling，IO 复杂度降低到了 $O(N^2 / \sqrt{M})$，其中 $M$ 是 SRAM 的大小。
  • 结论： 这证明了 FlashAttention 不仅仅是工程优化，在算法理论上也是 IO 最优的。

Page 46: 反向传播 (Backward Pass)

• 内容解析：
  • FlashAttention 的反向传播也使用了 重计算 (Recomputation) 技巧。
  • 前向传播时不保存 Attention 矩阵。
  • 反向传播时，利用保存的 $Q, K, V$ 和 Output，在 SRAM 中快速重新计算出 Attention 矩阵，用于梯度计算。
  • 虽然多算了，但省去了巨大的 HBM 写/读开销，总体速度更快。

Page 47: FlashAttention 2

• 内容解析：
  • 提到了后续版本 FlashAttention-2。
  • 进一步优化了并行策略（从并行化 Batch 变为并行化 Sequence），减少了非 MatMul 操作的开销，使得性能更接近硬件极限。

Page 48: 广泛应用

• 内容解析：
  • FlashAttention 已经成为所有现代 LLM 训练框架（PyTorch, MosaicML, DeepSpeed）的标配。
  • 它使得长上下文（Long Context）模型成为可能。

Page 49: Recap Part 1 (GPUs in Depth)

• 内容解析：
  • GPU 是为吞吐量设计的，拥有海量 ALU。
  • 内存层级（HBM vs SRAM）是理解性能的关键。
  • 执行模型（Grid/Block/Warp）决定了代码的组织方式。

Page 50: Recap Part 2 (Performance Optimization)

• 内容解析：
  • Roofline Model: 区分 Compute Bound 和 Memory Bound。
  • Optimization Tricks:
    1. Tiling: 利用 SRAM 复用数据。
    2. Coalescing: 对齐内存访问。
    3. Fusion: 减少 HBM 访问。
    4. Tensor Cores: 加速矩阵计算。

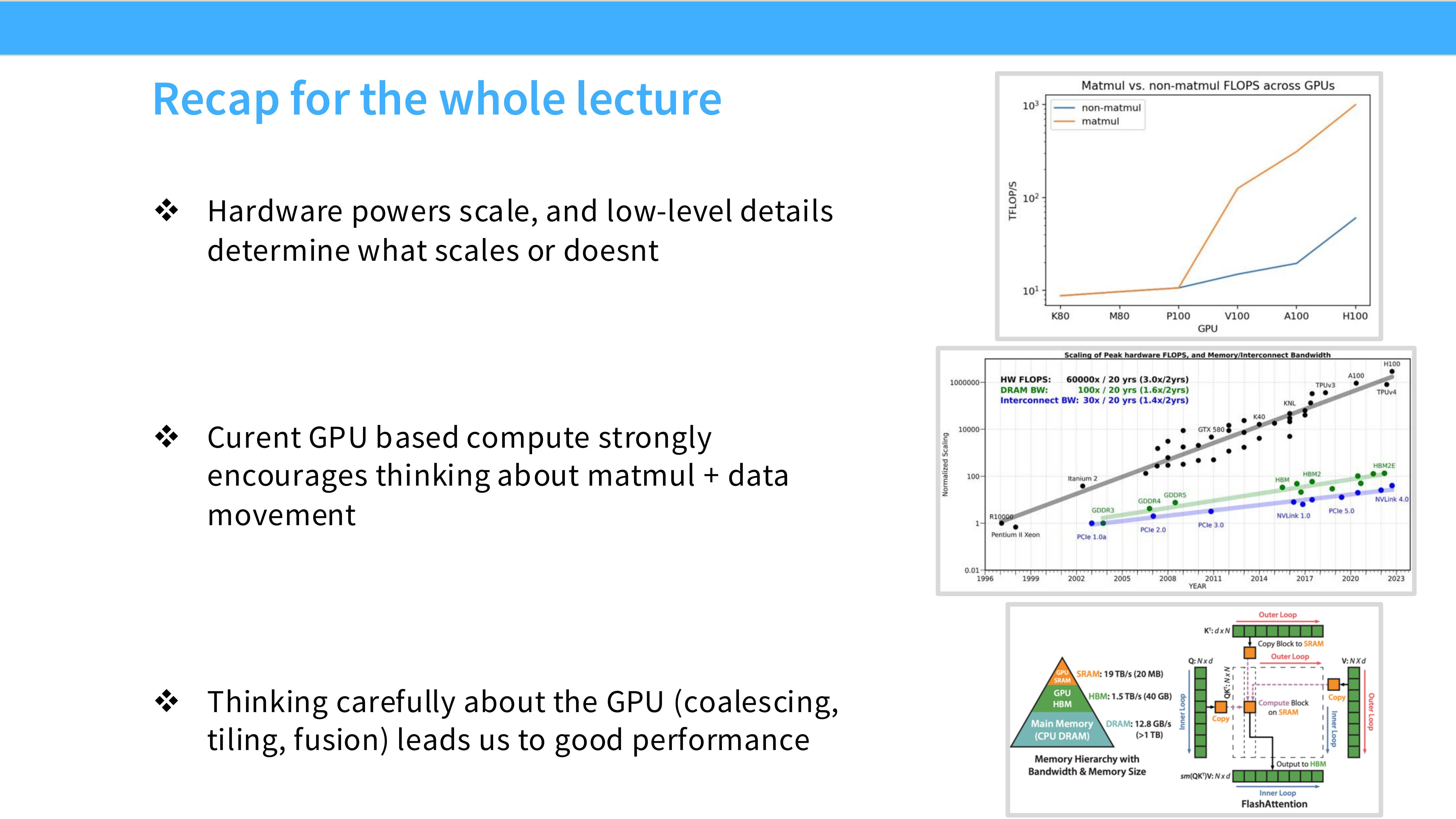
Page 51: 全课总结 (Recap for the whole lecture)

• 内容解析：
  1. Hardware: 硬件算力和底层细节（SRAM 带宽）决定了扩展的上限。
  2. Performance: 当前 GPU 编程的核心在于思考 MatMul + Data Movement。显存带宽通常是最大的瓶颈。
  3. Tricks: 仔细思考 GPU 特性 —— Coalescing, Tiling, Fusion —— 能带来巨大的性能提升。FlashAttention 就是这些原则的集大成者，它通过算法创新将一个 Memory Bound 的问题转化为了 Compute Bound 的问题。