大模型从0到1｜第二讲：PyTorch手把手搭建LLM

课程链接：Stanford CS336 Spring 2025 - Lecture 2

---

课程概述

上节课回顾： 课程概述、Tokenization

本讲概览：

• 讨论训练模型所需的所有原语（primitives）
• 自底向上：从张量 → 模型 → 优化器 → 训练循环
• 密切关注效率（资源使用）

两类资源：

1. 内存（Memory） - GB
2. 计算（Compute） - FLOPs

---

动机问题

让我们做一些粗略计算：

问题 1：训练时间估算

问题： 在 1024 个 H100 上训练 70B 参数模型，使用 15T token，需要多长时间？

# 总 FLOPs = 6 × 参数量 × token 数
total_flops = 6 * 70e9 * 15e12  # 6.3e24 FLOPs

# H100 性能
h100_flop_per_sec = 1979e12 / 2  # 989.5 TFLOP/s（无稀疏性）

# 模型 FLOPs 利用率（MFU）
mfu = 0.5

# 每天的 FLOPs
flops_per_day = h100_flop_per_sec * mfu * 1024 * 60 * 60 * 24
# ≈ 4.37e22 FLOPs/day

# 所需天数
days = total_flops / flops_per_day  # ≈ 144 天

---

问题 2：内存容量估算

问题： 使用 AdamW 在 8 个 H100 上能训练多大的模型？

# H100 内存
h100_bytes = 80e9  # 80 GB

# 每个参数的字节数
bytes_per_parameter = 4 + 4 + (4 + 4)  # 16 bytes
# - 参数：4 bytes (float32)
# - 梯度：4 bytes (float32)
# - 优化器状态：8 bytes (m, v for Adam)

# 可容纳的参数量
num_parameters = (h100_bytes * 8) / bytes_per_parameter
# ≈ 40B 参数

注意事项：

1. 可以使用 bf16 存储参数和梯度（2+2），保留 float32 副本（4），不节省内存但更快
2. 激活（activations）未计入（取决于批大小和序列长度）

这只是粗略的估算！

---

Part 1: 内存核算

1.1 张量基础

张量： 存储一切的基本构建块

• 参数（Parameters）
• 梯度（Gradients）
• 优化器状态（Optimizer State）
• 数据（Data）
• 激活（Activations）

文档： PyTorch Tensors

创建张量

# 方式 1：从列表创建
x = torch.tensor([[1., 2, 3], [4, 5, 6]])

# 方式 2：全零矩阵
x = torch.zeros(4, 8)  # 4x8 矩阵

# 方式 3：全一矩阵
x = torch.ones(4, 8)

# 方式 4：随机正态分布
x = torch.randn(4, 8)  # N(0, 1)

# 方式 5：分配但不初始化（更快）
x = torch.empty(4, 8)
# 稍后使用自定义逻辑初始化
nn.init.trunc_normal_(x, mean=0, std=1, a=-2, b=2)

---

1.2 浮点数类型

几乎所有内容（参数、梯度、激活、优化器状态）都存储为浮点数。

float32（单精度）

特点：

• 默认数据类型
• 1 位符号 + 8 位指数 + 23 位尾数
• 每个值 4 字节

示例：

x = torch.zeros(4, 8)
assert x.dtype == torch.float32  # 默认类型
assert x.numel() == 32  # 元素数量
assert x.element_size() == 4  # 每个元素 4 字节
assert x.numel() * x.element_size() == 128  # 总共 128 字节

GPT-3 的一个前馈层矩阵：

# 12288 * 4 × 12288 = 2.3 GB
torch.empty(12288 * 4, 12288).numel() * 4 / (1024**3)  # 2.3 GB

这太多了！

---

float16（半精度）

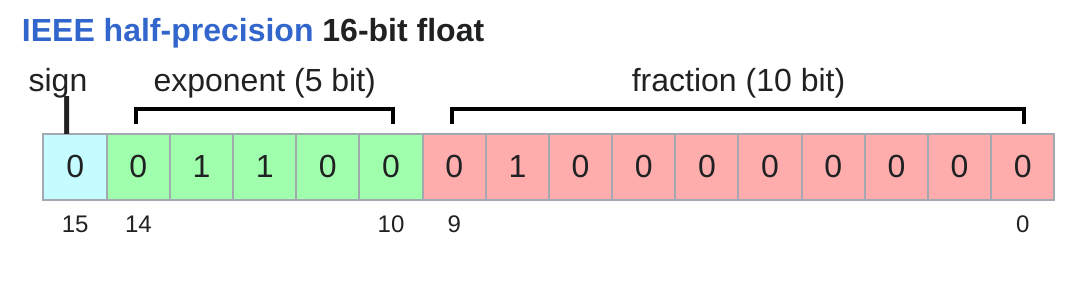
特点：

• 1 位符号 + 5 位指数 + 10 位尾数
• 每个值 2 字节
• 内存减半

问题：动态范围不足

x = torch.tensor([1e-8], dtype=torch.float16)
assert x == 0  # 下溢！

训练时可能导致不稳定。

---

bfloat16（Brain Float）

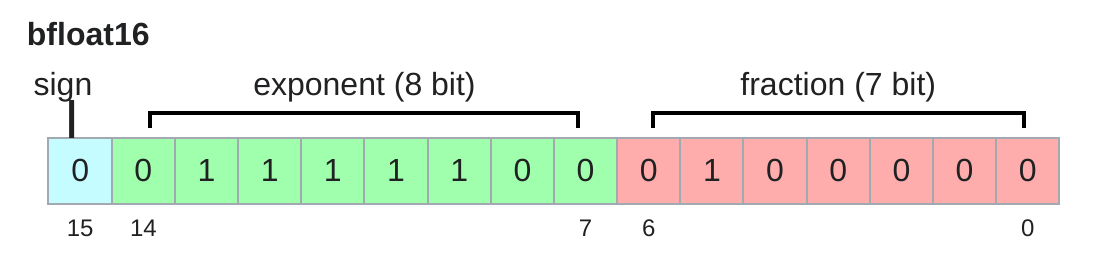
特点：

• Google Brain 2018 年开发
• 1 位符号 + 8 位指数 + 7 位尾数
• 与 float16 相同内存（2 字节）
• 与 float32 相同动态范围！
• 只是精度较低（但深度学习不太在意）

x = torch.tensor([1e-8], dtype=torch.bfloat16)
assert x != 0  # 没有下溢！

对比：

float32_info = torch.finfo(torch.float32)
# max=3.4e38, min=-3.4e38, eps=1.19e-07

float16_info = torch.finfo(torch.float16)
# max=65504, min=-65504, eps=0.000977

bfloat16_info = torch.finfo(torch.bfloat16)
# max=3.39e38, min=-3.39e38, eps=0.0078

---

FP8

2022 年标准化，专为机器学习设计

H100 支持两种 FP8 变体：

• E4M3： 范围 [-448, 448]
• E5M2： 范围 [-57344, 57344]

参考： FP8 Formats for Deep Learning

---

训练的影响

问题：

• float32 训练可行，但需要大量内存
• fp8、float16 甚至 bfloat16 训练有风险，可能不稳定

解决方案： 混合精度训练（稍后讨论）

---

1.3 GPU 上的张量

默认： 张量存储在 CPU 内存中

x = torch.zeros(32, 32)
assert x.device == torch.device("cpu")

GPU 加速： 需要将张量移动到 GPU 内存

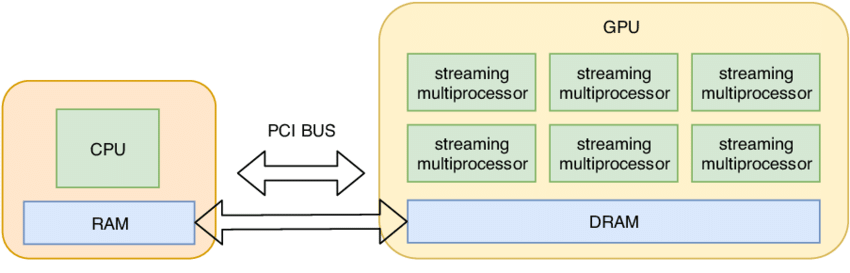
检查 GPU

# 检查是否有 GPU
torch.cuda.is_available()  # True/False

# GPU 数量
num_gpus = torch.cuda.device_count()

# GPU 属性
for i in range(num_gpus):
    properties = torch.cuda.get_device_properties(i)
    # name, total_memory, etc.

# 当前内存使用
memory_allocated = torch.cuda.memory_allocated()

移动到 GPU

# 方式 1：移动现有张量
x = torch.zeros(32, 32)
y = x.to("cuda:0")
assert y.device == torch.device("cuda", 0)

# 方式 2：直接在 GPU 上创建
z = torch.zeros(32, 32, device="cuda:0")

# 检查内存使用
new_memory = torch.cuda.memory_allocated()
memory_used = new_memory - memory_allocated
assert memory_used == 2 * (32 * 32 * 4)  # 两个 32x32 float32 矩阵

---

1.4 张量存储机制

PyTorch 张量 = 指向内存的指针 + 元数据

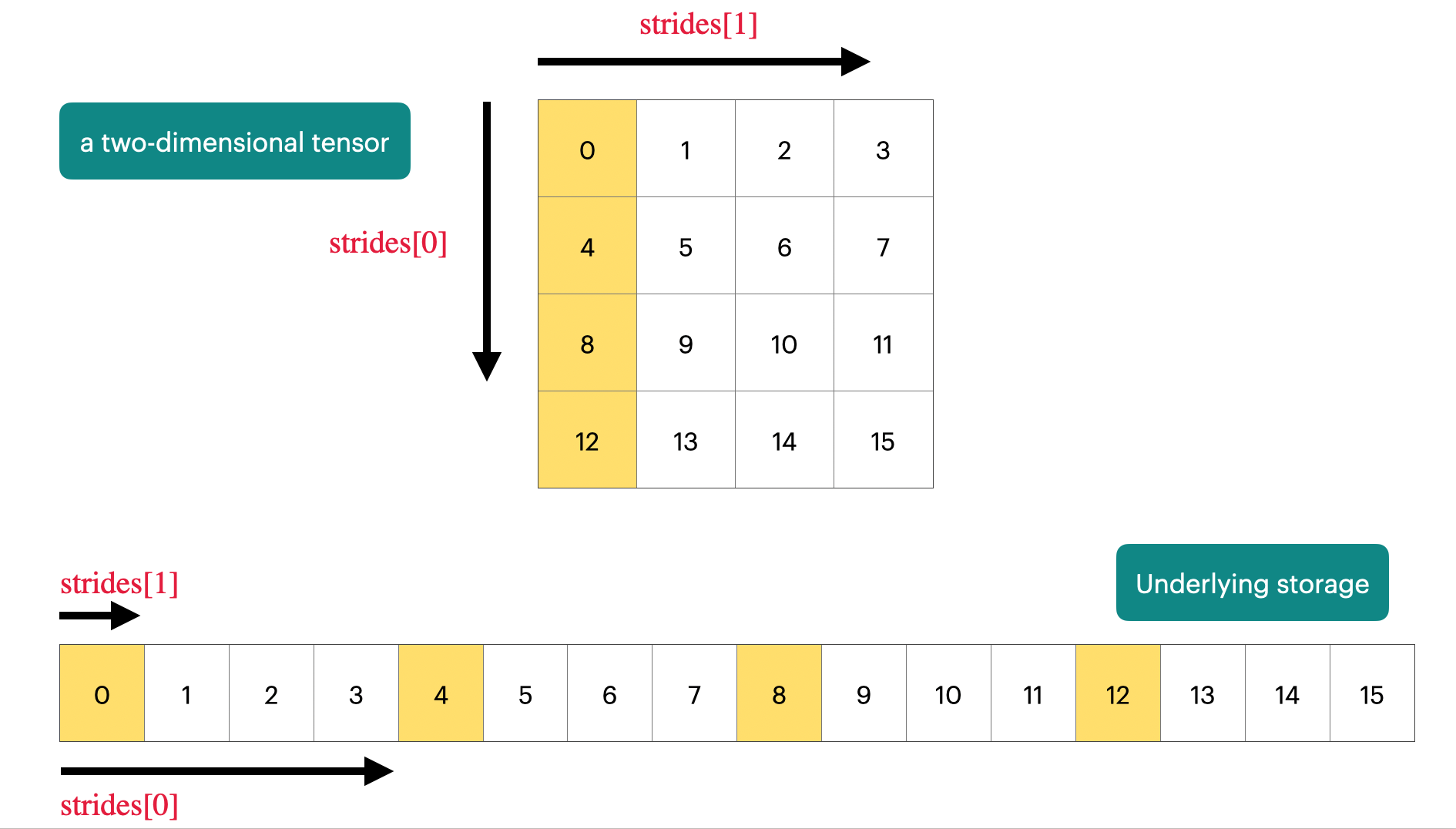
Stride（步长）： 描述如何访问任何元素

x = torch.tensor([
    [0., 1, 2, 3],
    [4, 5, 6, 7],
    [8, 9, 10, 11],
    [12, 13, 14, 15],
])

# 下一行：跳过 4 个元素
assert x.stride(0) == 4

# 下一列：跳过 1 个元素
assert x.stride(1) == 1

# 访问元素 [1, 2]
r, c = 1, 2
index = r * x.stride(0) + c * x.stride(1)  # 1*4 + 2*1 = 6
assert x.storage()[index] == 6.0

---

1.5 张量视图（Views）

许多操作只是提供张量的不同视图，不复制数据。

切片

x = torch.tensor([[1., 2, 3], [4, 5, 6]])

# 获取第 0 行
y = x[0]  # [1., 2., 3.]
assert same_storage(x, y)  # 共享存储！

# 获取第 1 列
y = x[:, 1]  # [2., 5.]
assert same_storage(x, y)

重塑

# 2x3 → 3x2
y = x.view(3, 2)  # [[1, 2], [3, 4], [5, 6]]
assert same_storage(x, y)

# 转置
y = x.transpose(1, 0)  # [[1, 4], [2, 5], [3, 6]]
assert same_storage(x, y)

突变共享

x[0][0] = 100
# y 也会改变！
assert y[0][0] == 100

---

连续性（Contiguity）

某些视图是非连续的，无法进一步视图化：

x = torch.tensor([[1., 2, 3], [4, 5, 6]])
y = x.transpose(1, 0)
assert not y.is_contiguous()

# 尝试 view 会失败
try:
    y.view(2, 3)
except RuntimeError:
    # "view size is not compatible..."
    pass

# 解决方案：先使其连续
y = x.transpose(1, 0).contiguous().view(2, 3)
assert not same_storage(x, y)  # 现在是副本

权衡：

• 视图：免费，无额外内存/计算
• 复制：需要额外内存和计算

---

Part 2: 计算核算

2.1 张量操作

大多数张量是通过对其他张量执行操作创建的。

每个操作都有内存和计算后果。

逐元素操作

对张量的每个元素应用操作，返回相同形状的张量：

x = torch.tensor([1, 4, 9])

# 幂运算
x.pow(2)  # [1, 16, 81]

# 平方根
x.sqrt()  # [1, 2, 3]

# 倒数平方根
x.rsqrt()  # [1, 1/2, 1/3]

# 算术运算
x + x  # [2, 8, 18]
x * 2  # [2, 8, 18]
x / 0.5  # [2, 8, 18]

上三角矩阵：

x = torch.ones(3, 3).triu()
# [[1, 1, 1],
#  [0, 1, 1],
#  [0, 0, 1]]

用于计算因果注意力掩码，其中 M[i, j] 是 i 对 j 的贡献。

---

矩阵乘法

深度学习的核心：

x = torch.ones(16, 32)
w = torch.ones(32, 2)
y = x @ w
assert y.size() == torch.Size([16, 2])

批处理和序列：

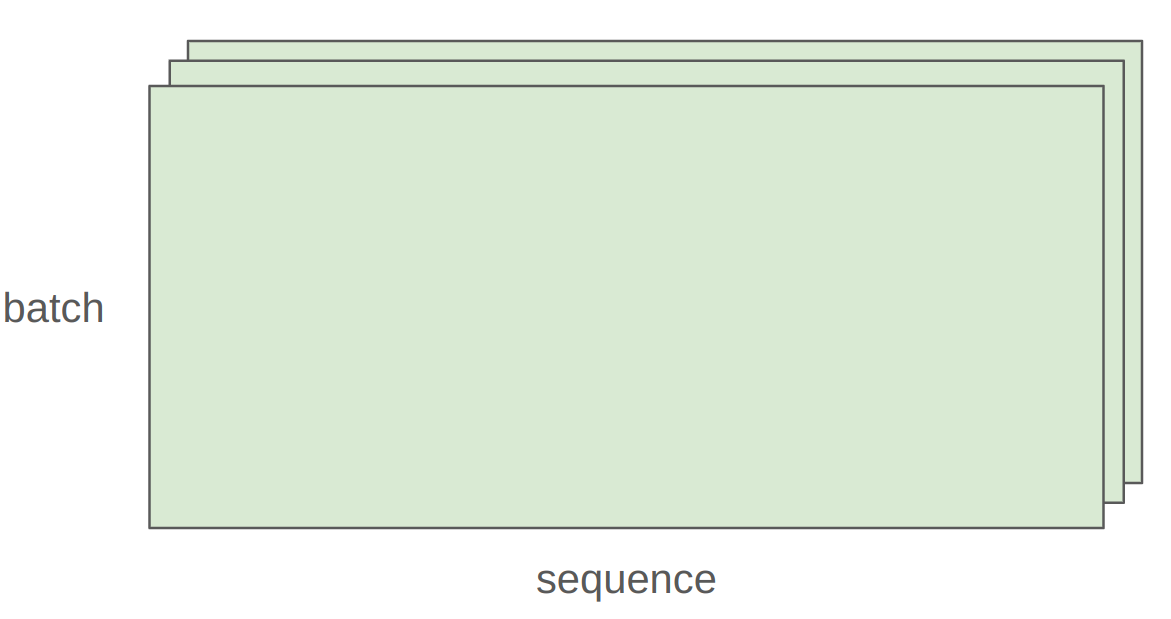
# batch=4, seq=8, input_dim=16, output_dim=2
x = torch.ones(4, 8, 16, 32)
w = torch.ones(32, 2)
y = x @ w
assert y.size() == torch.Size([4, 8, 16, 2])

迭代前两个维度，每个与 w 相乘。

---

2.2 Einops：优雅的张量操作

动机： 传统 PyTorch 代码容易出错

# 传统方式
x = torch.ones(2, 2, 3)  # batch, sequence, hidden
y = torch.ones(2, 2, 3)
z = x @ y.transpose(-2, -1)  # -2, -1 是什么？

Einops： 受 Einstein 求和记号启发（1916）

Einops Tutorial

---

JaxTyping：维度标注

旧方式：

x = torch.ones(2, 2, 1, 3)  # batch seq heads hidden

新方式（JaxTyping）：

from jaxtyping import Float

x: Float[torch.Tensor, "batch seq heads hidden"] = torch.ones(2, 2, 1, 3)

注意：这只是文档（无强制执行）

---

Einsum：广义矩阵乘法

from einops import einsum

x: Float[torch.Tensor, "batch seq1 hidden"] = torch.ones(2, 3, 4)
y: Float[torch.Tensor, "batch seq2 hidden"] = torch.ones(2, 3, 4)

# 旧方式
z = x @ y.transpose(-2, -1)

# 新方式（Einops）
z = einsum(x, y, "batch seq1 hidden, batch seq2 hidden -> batch seq1 seq2")

规则： 输出中未命名的维度会被求和。

广播： 使用 ... 表示任意数量的维度

z = einsum(x, y, "... seq1 hidden, ... seq2 hidden -> ... seq1 seq2")

---

Reduce：归约操作

from einops import reduce

x: Float[torch.Tensor, "batch seq hidden"] = torch.ones(2, 3, 4)

# 旧方式
y = x.mean(dim=-1)

# 新方式（Einops）
y = reduce(x, "... hidden -> ...", "mean")
# 也支持：sum, max, min

---

Rearrange：重塑维度

有时一个维度代表两个维度，你想单独操作其中一个。

from einops import rearrange

x: Float[torch.Tensor, "batch seq total_hidden"] = torch.ones(2, 3, 8)
# total_hidden 是 heads * hidden1 的扁平表示

w: Float[torch.Tensor, "hidden1 hidden2"] = torch.ones(4, 4)

# 步骤 1：分解 total_hidden
x = rearrange(x, "... (heads hidden1) -> ... heads hidden1", heads=2)
# 现在 x.shape = (2, 3, 2, 4)

# 步骤 2：应用变换
x = einsum(x, w, "... hidden1, hidden1 hidden2 -> ... hidden2")

# 步骤 3：合并回去
x = rearrange(x, "... heads hidden2 -> ... (heads hidden2)")

---

2.3 FLOPs 计算

FLOP（浮点运算）： 基本操作如加法（x + y）或乘法（x * y）

两个容易混淆的缩写：

• FLOPs： 浮点运算数量（计算量的度量）
• FLOP/s（或 FLOPS）： 每秒浮点运算数（硬件速度的度量）

---

直觉

训练成本：

• GPT-3 (2020)：3.14e23 FLOPs
• GPT-4 (2023)：推测 2e25 FLOPs
• 美国行政命令（2025 年撤销）：≥1e26 FLOPs 的模型必须向政府报告

硬件性能：

• A100：312 TFLOP/s（峰值）
• H100：1979 TFLOP/s（带稀疏性），989.5 TFLOP/s（无稀疏性）

8 个 H100 运行 2 周：

total_flops = 8 * (60 * 60 * 24 * 14) * 989.5e12
# ≈ 6.8e21 FLOPs

---

线性模型示例

B = 16384  # 数据点数量
D = 32768  # 维度
K = 8192   # 输出数量

x = torch.ones(B, D, device="cuda")
w = torch.randn(D, K, device="cuda")
y = x @ w

FLOPs 计算：

• 每个 (i, j, k) 三元组：1 次乘法 + 1 次加法
• 总 FLOPs = 2 * B * D * K

actual_num_flops = 2 * 16384 * 32768 * 8192
# ≈ 8.8e15 FLOPs

---

其他操作的 FLOPs

• 逐元素操作： O(m * n) FLOPs（m×n 矩阵）
• 矩阵加法： m * n FLOPs

关键洞察： 对于足够大的矩阵，没有其他操作比矩阵乘法更昂贵。

---

训练的 FLOPs

解释：

• B = token 数量
• (D * K) = 参数数量
• 前向传播 FLOPs = 2 × token 数 × 参数数

这推广到 Transformer（一阶近似）！

---

实际性能测试

import time

def time_matmul(x, w):
    # Warmup
    for _ in range(10):
        _ = x @ w
    torch.cuda.synchronize()
    
    # 计时
    start = time.time()
    for _ in range(100):
        _ = x @ w
    torch.cuda.synchronize()
    end = time.time()
    
    return (end - start) / 100

actual_time = time_matmul(x, w)  # 例如 0.002 秒
actual_flop_per_sec = actual_num_flops / actual_time
# 例如 4.4e18 FLOP/s

---

模型 FLOPs 利用率（MFU）

定义： MFU = 实际 FLOP/s / 承诺 FLOP/s

promised_flop_per_sec = 989.5e12  # H100 无稀疏性
mfu = actual_flop_per_sec / promised_flop_per_sec
# 例如 0.44（44%）

通常 MFU ≥ 0.5 就很好了（如果矩阵乘法占主导会更高）

---

bfloat16 性能

x = x.to(torch.bfloat16)
w = w.to(torch.bfloat16)

bf16_actual_time = time_matmul(x, w)
bf16_actual_flop_per_sec = actual_num_flops / bf16_actual_time
bf16_promised_flop_per_sec = 1979e12  # H100 bf16 峰值
bf16_mfu = bf16_actual_flop_per_sec / bf16_promised_flop_per_sec

观察：

• bfloat16 的实际 FLOP/s 更高
• MFU 可能较低（承诺的 FLOPs 有点乐观）

---

2.4 梯度计算

基础示例

简单线性模型：y = 0.5 * (x * w - 5)²

# 前向传播
x = torch.tensor([1., 2, 3])
w = torch.tensor([1., 1, 1], requires_grad=True)
pred_y = x @ w
loss = 0.5 * (pred_y - 5).pow(2)

# 反向传播
loss.backward()

# 检查梯度
assert loss.grad is None
assert pred_y.grad is None
assert x.grad is None
assert torch.equal(w.grad, torch.tensor([1, 2, 3]))

---

梯度的 FLOPs

模型： x –w1–> h1 –w2–> h2 -> loss

B = 16384  # 批大小
D = 32768  # 维度
K = 8192   # 输出维度

x = torch.ones(B, D, device="cuda")
w1 = torch.randn(D, D, device="cuda", requires_grad=True)
w2 = torch.randn(D, K, device="cuda", requires_grad=True)

h1 = x @ w1
h2 = h1 @ w2
loss = h2.pow(2).mean()

前向 FLOPs：

num_forward_flops = (2 * B * D * D) + (2 * B * D * K)

反向传播：

h1.retain_grad()
h2.retain_grad()
loss.backward()

计算 w2.grad：

w2.grad[j,k] = sum_i h1[i,j] * h2.grad[i,k]

• FLOPs = 2 * B * D * K

计算 h1.grad：

h1.grad[i,j] = sum_k w2[j,k] * h2.grad[i,k]

• FLOPs = 2 * B * D * K

w1 同理：

• FLOPs = (2 + 2) * B * D * D

总反向 FLOPs：

num_backward_flops = 4 * B * D * D + 4 * B * D * K

---

可视化

Blog Post: FLOPs Calculus

---

总结

训练一步的 FLOPs：

• 前向传播：2 × token 数 × 参数数
• 反向传播：4 × token 数 × 参数数
• 总计：6 × token 数 × 参数数

---

Part 3: 模型

3.1 参数

模型参数在 PyTorch 中存储为 nn.Parameter 对象。

input_dim = 16384
output_dim = 32

w = nn.Parameter(torch.randn(input_dim, output_dim))
assert isinstance(w, torch.Tensor)  # 行为像张量
assert type(w.data) == torch.Tensor  # 访问底层张量

---

3.2 参数初始化

问题： 未缩放的初始化

x = nn.Parameter(torch.randn(input_dim))
output = x @ w

# 每个元素的规模为 sqrt(input_dim)
# 大值会导致梯度爆炸，训练不稳定

解决方案： 缩放使其与 input_dim 无关

w = nn.Parameter(torch.randn(input_dim, output_dim) / np.sqrt(input_dim))
output = x @ w
# 现在每个元素的规模是常数

Xavier 初始化：

• Paper
• 截断正态分布到 [-3, 3] 以避免异常值

w = nn.Parameter(
    nn.init.trunc_normal_(
        torch.empty(input_dim, output_dim),
        std=1 / np.sqrt(input_dim),
        a=-3, b=3
    )
)

---

3.3 自定义模型

简单线性层

class Linear(nn.Module):
    def __init__(self, input_dim: int, output_dim: int):
        super().__init__()
        self.weight = nn.Parameter(
            torch.randn(input_dim, output_dim) / np.sqrt(input_dim)
        )

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        return x @ self.weight

---

深度线性模型

class Cruncher(nn.Module):
    def __init__(self, dim: int, num_layers: int):
        super().__init__()
        self.layers = nn.ModuleList([
            Linear(dim, dim)
            for i in range(num_layers)
        ])
        self.final = Linear(dim, 1)

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        # 应用线性层
        for layer in self.layers:
            x = layer(x)
        
        # 应用最终层
        x = self.final(x)
        
        # 移除最后一个维度
        x = x.squeeze(-1)
        return x

---

使用模型

D = 64
num_layers = 2
model = Cruncher(dim=D, num_layers=num_layers)

# 检查参数
param_sizes = [
    (name, param.numel())
    for name, param in model.state_dict().items()
]
# [('layers.0.weight', D*D),
#  ('layers.1.weight', D*D),
#  ('final.weight', D)]

num_parameters = sum(p.numel() for p in model.parameters())
# D*D + D*D + D

# 移动到 GPU
device = "cuda" if torch.cuda.is_available() else "cpu"
model = model.to(device)

# 运行模型
B = 8
x = torch.randn(B, D, device=device)
y = model(x)
assert y.size() == torch.Size([B])

---

Part 4: 训练循环

4.1 随机性注意事项

随机性出现在许多地方：

• 参数初始化
• Dropout
• 数据顺序

为了可重现性，始终设置随机种子：

seed = 0

# PyTorch
torch.manual_seed(seed)

# NumPy
import numpy as np
np.random.seed(seed)

# Python
import random
random.seed(seed)

确定性对调试特别有用！

---

4.2 数据加载

语言建模数据： 整数序列（tokenizer 输出）

序列化为 NumPy 数组：

# 保存
data = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10], dtype=np.int32)
data.tofile("data.npy")

# 加载（使用 memmap 懒加载）
data = np.memmap("data.npy", dtype=np.int32)
# 不会一次性加载所有数据到内存
# LLaMA 数据是 2.8TB！

---

批处理函数

def get_batch(data, batch_size, sequence_length, device):
    # 随机采样 batch_size 个位置
    start_indices = torch.randint(
        len(data) - sequence_length,
        (batch_size,)
    )
    
    # 索引数据
    x = torch.tensor([
        data[start:start + sequence_length]
        for start in start_indices
    ])
    
    # Pinned memory（可选，用于异步传输）
    if torch.cuda.is_available():
        x = x.pin_memory()
    
    # 移动到 GPU（非阻塞）
    x = x.to(device, non_blocking=True)
    
    return x

Pinned Memory 优势：

• 允许 CPU → GPU 异步复制
• 可以并行：
  • 在 CPU 上获取下一批数据
  • 在 GPU 上处理当前批次

---

4.3 优化器

SGD（随机梯度下降）

class SGD(torch.optim.Optimizer):
    def __init__(self, params, lr=0.01):
        super().__init__(params, dict(lr=lr))

    def step(self):
        for group in self.param_groups:
            lr = group["lr"]
            for p in group["params"]:
                grad = p.grad.data
                p.data -= lr * grad

---

AdaGrad

class AdaGrad(torch.optim.Optimizer):
    def __init__(self, params, lr=0.01):
        super().__init__(params, dict(lr=lr))

    def step(self):
        for group in self.param_groups:
            lr = group["lr"]
            for p in group["params"]:
                state = self.state[p]
                grad = p.grad.data
                
                # 获取累积平方梯度
                g2 = state.get("g2", torch.zeros_like(grad))
                
                # 更新优化器状态
                g2 += torch.square(grad)
                state["g2"] = g2
                
                # 更新参数
                p.data -= lr * grad / torch.sqrt(g2 + 1e-5)

---

优化器层次

• Momentum = SGD + 梯度的指数平均
• AdaGrad = SGD + 按 grad² 平均
• RMSProp = AdaGrad + grad² 的指数平均
• Adam = RMSProp + Momentum

---

使用优化器

model = Cruncher(dim=4, num_layers=2).to(device)
optimizer = AdaGrad(model.parameters(), lr=0.01)

# 前向传播
x = torch.randn(2, 4, device=device)
y = torch.tensor([4., 5.], device=device)
pred_y = model(x)
loss = F.mse_loss(pred_y, y)

# 反向传播
loss.backward()

# 更新参数
optimizer.step()

# 清零梯度
optimizer.zero_grad(set_to_none=True)

---

4.4 资源核算

内存（float32）：

# 参数
num_parameters = D*D*num_layers + D

# 激活
num_activations = B * D * num_layers

# 梯度
num_gradients = num_parameters

# 优化器状态（AdaGrad）
num_optimizer_states = num_parameters

# 总内存
total_memory = 4 * (
    num_parameters +
    num_activations +
    num_gradients +
    num_optimizer_states
)

计算（一步）：

flops = 6 * B * num_parameters

Transformer 更复杂，但思路相同。

参考：

• Transformer Memory
• Transformer FLOPs

---

4.5 训练循环

def train(get_batch, D, num_layers, B, num_train_steps, lr):
    model = Cruncher(dim=D, num_layers=num_layers).to(device)
    optimizer = SGD(model.parameters(), lr=lr)
    
    for t in range(num_train_steps):
        # 获取数据
        x, y = get_batch(B=B)
        
        # 前向传播
        pred_y = model(x)
        loss = F.mse_loss(pred_y, y)
        
        # 反向传播
        loss.backward()
        
        # 更新参数
        optimizer.step()
        optimizer.zero_grad(set_to_none=True)

---

4.6 检查点（Checkpointing）

训练需要很长时间，肯定会崩溃。不想失去所有进度！

定期保存模型和优化器状态：

model = Cruncher(dim=64, num_layers=3).to(device)
optimizer = AdaGrad(model.parameters(), lr=0.01)

# 保存检查点
checkpoint = {
    "model": model.state_dict(),
    "optimizer": optimizer.state_dict(),
}
torch.save(checkpoint, "model_checkpoint.pt")

# 加载检查点
loaded_checkpoint = torch.load("model_checkpoint.pt")
model.load_state_dict(loaded_checkpoint["model"])
optimizer.load_state_dict(loaded_checkpoint["optimizer"])

---

4.7 混合精度训练

权衡：

• 高精度：更准确/稳定，更多内存，更多计算
• 低精度：不太准确/稳定，更少内存，更少计算

如何两全其美？

解决方案： 默认使用 float32，但在可能的地方使用 {bfloat16, fp8}

具体计划：

• 前向传播使用 {bfloat16, fp8}（激活）
• 其余使用 float32（参数、梯度）

参考：

• Mixed Precision Training Paper
• PyTorch AMP
• NVIDIA Mixed Precision

NVIDIA Transformer Engine：

• 支持线性层的 FP8
• 在整个训练中普遍使用 FP8

---

总结

知识类型

机制（Mechanics）： 直接（只是 PyTorch）

• 张量操作
• 模型定义
• 训练循环

思维方式（Mindset）： 资源核算（记得做）

• 内存：参数 + 激活 + 梯度 + 优化器状态
• 计算：6 × token 数 × 参数数

直觉（Intuitions）： 大致方向（没有大模型）

• 初始化很重要
• 数据类型权衡
• MFU 作为效率指标

---

关键要点

1. 张量是一切的基础

   • 理解存储和视图
   • 注意数据类型

2. 资源核算至关重要

   • 内存：每个参数 16 字节（AdamW）
   • 计算：6 × tokens × params FLOPs

3. 效率驱动设计

   • 混合精度训练
   • 参数初始化
   • 批处理和数据加载

---

下节课预告

主题： Transformer 架构细节

---

参考资源

PyTorch 文档：

• Tensors
• Automatic Mixed Precision

Einops：

• Tutorial
• GitHub

博客文章：

• Transformer Memory
• Transformer FLOPs
• FLOPs Calculus

论文：

• Xavier Initialization
• Mixed Precision Training
• FP8 Formats